Теория кривых. Плоские кривые презентация

Содержание

1. Теория кривых. Плоские кривые
2. Плоские кривые Пусть кривая целиком лежит в
3. Плоские кривые Из (29) выразим y:
4. Особые точки плоской кривой Определение: точка
5. Классификация особых точек плоской кривой Обозначим
6. Рассмотрим (33) в особой точке: Классификация особых
7. Б. 1) Уравнение (34’) имеет 2
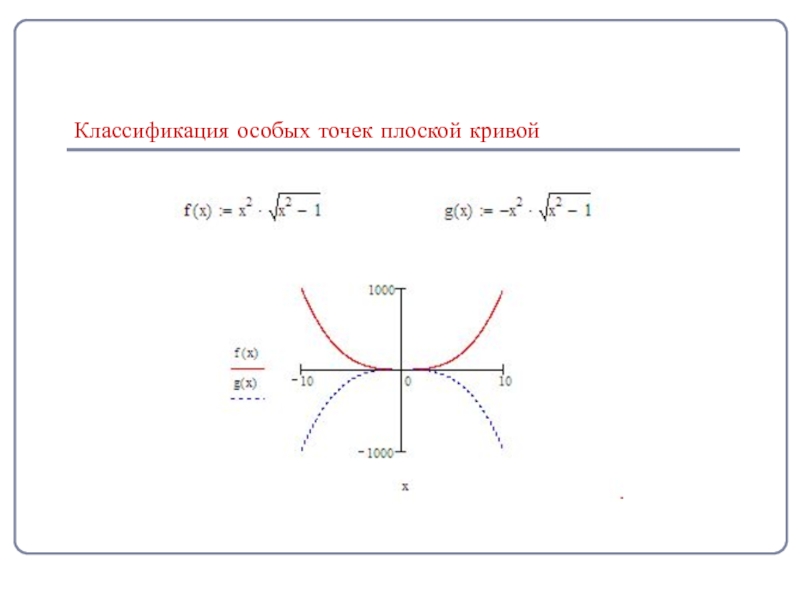
8. Классификация особых точек плоской кривой
9. Классификация особых точек плоской кривой
10. Классификация особых точек плоской кривой 2) Точка
11. Классификация особых точек плоской кривой 3) Точка
12. 4) Точка самоприкосновения 5) Классификация особых точек плоской кривой
13. Однопараметрическое семейство плоских кривых (ОСПК) Определение: однопараметрическим
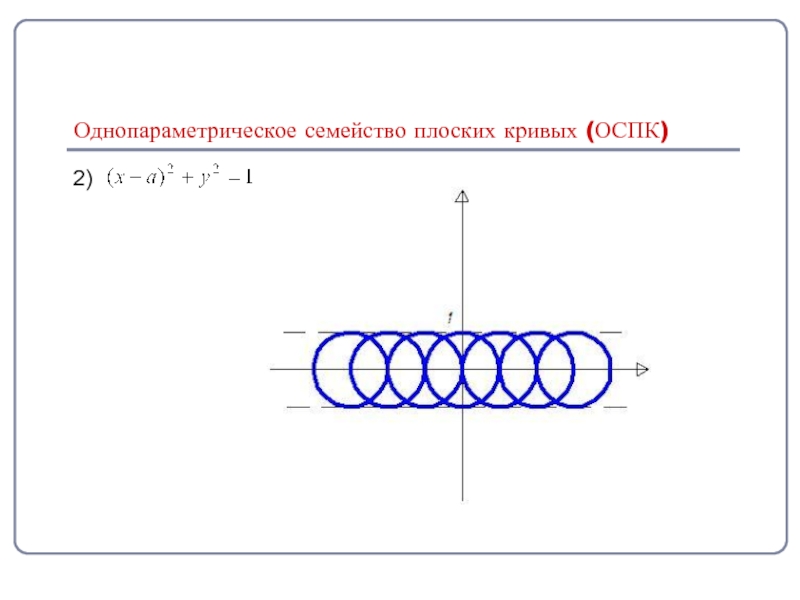
14. 2) Однопараметрическое семейство плоских кривых (ОСПК)
15. Однопараметрическое семейство плоских кривых (ОСПК) Определение: плоская
16. Однопараметрическое семейство плоских кривых (ОСПК) Теорема 1.
17. Однопараметрическое семейство плоских кривых (ОСПК)
18. , следовательно, огибающая удовлетворяет
19. 2) Пусть - дискриминантная
20. (35) где а – параметр.
21. (35) где а – параметр.
22. (31)
23. Определение: однопараметрическим
24. (31)
25. (31)
26. (29) (29) – неявное уравнение плоской кривой.

Плоские кривые Пусть кривая целиком лежит в плоскости xOy. Кривая задана: - параметрическое задание кривой (28) (28) – параметрическое задание плоской кривой. Из (28) исключим t:

Главная
Математика
Теория кривых. Плоские кривые

Слайд 1ТЕОРИЯ КРИВЫХ
Плоские кривые

Слайд 2Плоские кривые
Пусть кривая целиком лежит в плоскости xOy.
Кривая задана:

- параметрическое

задание кривой

(28)

(28) – параметрическое задание плоской кривой.

Из (28) исключим t:

(29)

(29) – неявное уравнение плоской кривой.

Слайд 3Плоские кривые
Из (29) выразим y:

(30)
(30) – задание явной функции в виде

графика.

Вычислим

(она равна 0):

Обозначим:

(31)

Слайд 4Особые точки плоской кривой
Определение: точка
называется особой точкой
плоской кривой, заданной неявным

уравнением,
если в ней выполняются равенства:

(32)

Если

- не особая точка, то из (31):

- угловой коэффициент касательной.

В особой точке k по формуле (31) не находится.

Проблема: нахождения углового коэффициента в особой точке.

Слайд 5Классификация особых точек плоской кривой
Обозначим

,
и подставим в уравнение (31):

(33)
продифференцируем по t

полученное равенство:

Обозначим

причем

Слайд 6Рассмотрим (33) в особой точке:
Классификация особых точек плоской кривой
(34)

:
А.

Уравнение (34’) не

имеет решений.

В точке нет касательной, следовательно, точка

изолированная.

Слайд 7Б.
1)

Уравнение (34’) имеет 2 решения.
Имеет 2 касательные, следовательно, через точку
В.
проходит

2 ветви кривой. Точка

называется узловой.

- изолированная.

Пример:

Классификация особых точек плоской кривой

Слайд 8Классификация особых точек плоской кривой

Последние две точки не принадлежат кривой, следовательно,
точка

(0;0) - особая

Слайд 9Классификация особых точек плоской кривой

Слайд 10Классификация особых точек плоской кривой
2)
Точка возврата 1-го рода.
В особой точке обе

ветви кривой имеют общую касательную,
но находятся по одну сторону от нормали, и по разные
стороны от касательной.

Пример:

- кубическая парабола

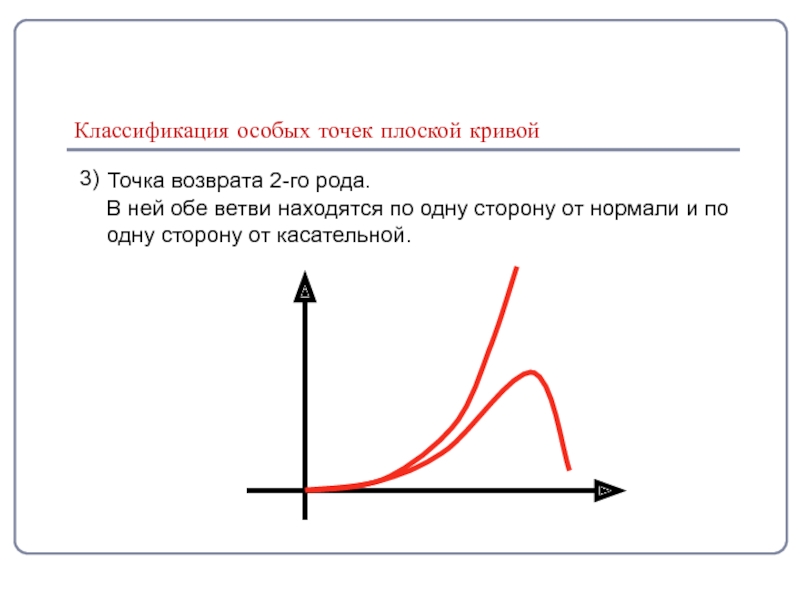
Слайд 11Классификация особых точек плоской кривой
3)
Точка возврата 2-го рода.
В ней

обе ветви находятся по одну сторону от нормали и по
одну сторону от касательной.

Слайд 124) Точка самоприкосновения

5)

Классификация особых точек плоской кривой

Слайд 13Однопараметрическое семейство плоских кривых (ОСПК)
Определение: однопараметрическим семейством плоских

кривых называется множество кривых на
плоскости, удовлетворяющих неявному уравнению:

(35)

где а – параметр.

Примеры:

Слайд 142)
Однопараметрическое семейство плоских кривых (ОСПК)

Слайд 15Однопараметрическое семейство плоских кривых (ОСПК)
Определение: плоская кривая, которая в каждой своей

точке
касается некоторой кривой однопараметрического
семейства кривых, называется огибающей этого
семейства.

Определение: кривая на плоскости, удовлетворяющая системе
уравнений:

(36)

где

уравнения ОПСК, называется

дискриминантной кривой семейства.

Слайд 16Однопараметрическое семейство плоских кривых (ОСПК)
Теорема 1.
Огибающая ОСПК, если она существует,

является
дискриминантной кривой этого ОСПК,
Любая дискриминантная кривая ОСПК является огибающей,
если она не состоит из особых точек кривых семейства.

Доказательство:

Пусть

(37)

(37) – огибающая ОСПК с уравнением (35).

Продифференцируем уравнение (35) по параметру а:

Слайд 17Однопараметрическое семейство плоских кривых (ОСПК)

Рассмотрим точку касания некоторой кривой семейства

и

огибающей, так как кривые касаются, то у них в этой точке общая
касательная, следовательно:

в точке касания.

- а фиксировано.

(*)

Слайд 18

, следовательно, огибающая удовлетворяет системе
уравнений:

тогда огибающая есть дискриминантная кривая.
Однопараметрическое семейство

плоских кривых (ОСПК)

Слайд 192)
Пусть

- дискриминантная кривая семейства (35).

, следовательно, дискриминантная кривая
касается в

каждой своей точке некоторой кривой семейства,
она является огибающей. Но в уравнении (*) может быть

(*)

, следовательно, дискриминантная кривая состоит из

особых точек кривых семейства.

Ч.т.д.

Однопараметрическое семейство плоских кривых (ОСПК)

выход

Слайд 20
(35)
где а – параметр.

Слайд 21
(35)
где а – параметр.

Слайд 22
(31)

Слайд 23Определение: однопараметрическим

семейством плоских кривых
называется множество кривых
на плоскости, удовлетворяющих
неявному уравнению:

(35)

где а – параметр.

Слайд 24
(31)

Слайд 25
(31)

Слайд 26

(29)
(29) – неявное уравнение плоской кривой.

Скачать презентацию

Теория кривых. Плоские кривые презентация

Содержание

Слайд 1ТЕОРИЯ КРИВЫХ
Плоские кривые

Слайд 2Плоские кривые
Пусть кривая целиком лежит в плоскости xOy.
Кривая задана:

- параметрическое

Слайд 3Плоские кривые
Из (29) выразим y:

(30)
(30) – задание явной функции в виде

Слайд 4Особые точки плоской кривой
Определение: точка
называется особой точкой
плоской кривой, заданной неявным

Слайд 5Классификация особых точек плоской кривой
Обозначим

,
и подставим в уравнение (31):

(33)
продифференцируем по t

Слайд 6Рассмотрим (33) в особой точке:
Классификация особых точек плоской кривой
(34)

:
А.

Уравнение (34’) не

Слайд 7Б.
1)

Уравнение (34’) имеет 2 решения.
Имеет 2 касательные, следовательно, через точку
В.
проходит

Слайд 8Классификация особых точек плоской кривой

Последние две точки не принадлежат кривой, следовательно,
точка

Слайд 9Классификация особых точек плоской кривой

Слайд 10Классификация особых точек плоской кривой
2)
Точка возврата 1-го рода.
В особой точке обе

Слайд 11Классификация особых точек плоской кривой
3)
Точка возврата 2-го рода.
В ней

Слайд 124) Точка самоприкосновения

5)

Классификация особых точек плоской кривой

Слайд 13Однопараметрическое семейство плоских кривых (ОСПК)
Определение: однопараметрическим семейством плоских

Слайд 142)
Однопараметрическое семейство плоских кривых (ОСПК)

Слайд 15Однопараметрическое семейство плоских кривых (ОСПК)
Определение: плоская кривая, которая в каждой своей

Слайд 16Однопараметрическое семейство плоских кривых (ОСПК)
Теорема 1.
Огибающая ОСПК, если она существует,

Слайд 17Однопараметрическое семейство плоских кривых (ОСПК)

Рассмотрим точку касания некоторой кривой семейства

и

Слайд 18

, следовательно, огибающая удовлетворяет системе
уравнений:

тогда огибающая есть дискриминантная кривая.
Однопараметрическое семейство

Слайд 192)
Пусть

- дискриминантная кривая семейства (35).

, следовательно, дискриминантная кривая
касается в

Слайд 20
(35)
где а – параметр.

Слайд 21
(35)
где а – параметр.

Слайд 22
(31)

Слайд 23Определение: однопараметрическим

Слайд 24
(31)

Слайд 25
(31)

Слайд 26

(29)
(29) – неявное уравнение плоской кривой.

Обратная связь

Что такое ThePresentation.ru?

Теория кривых. Плоские кривые презентация

Содержание

Слайд 1ТЕОРИЯ КРИВЫХПлоские кривые

Слайд 2Плоские кривыеПусть кривая целиком лежит в плоскости xOy.Кривая задана: - параметрическое

Слайд 3Плоские кривыеИз (29) выразим y:(30)(30) – задание явной функции в виде

Слайд 4Особые точки плоской кривойОпределение: точка называется особой точкойплоской кривой, заданной неявным

Слайд 5Классификация особых точек плоской кривойОбозначим,и подставим в уравнение (31):(33)продифференцируем по t

Слайд 6Рассмотрим (33) в особой точке:Классификация особых точек плоской кривой(34):А.Уравнение (34’) не

Слайд 7Б.1)Уравнение (34’) имеет 2 решения. Имеет 2 касательные, следовательно, через точкуВ.проходит

Слайд 8Классификация особых точек плоской кривойПоследние две точки не принадлежат кривой, следовательно,точка

Слайд 9Классификация особых точек плоской кривой

Слайд 10Классификация особых точек плоской кривой2)Точка возврата 1-го рода.В особой точке обе

Слайд 11Классификация особых точек плоской кривой3)Точка возврата 2-го рода. В ней

Слайд 124) Точка самоприкосновения5)Классификация особых точек плоской кривой

Слайд 13Однопараметрическое семейство плоских кривых (ОСПК)Определение: однопараметрическим семейством плоских

Слайд 142)Однопараметрическое семейство плоских кривых (ОСПК)

Слайд 15Однопараметрическое семейство плоских кривых (ОСПК)Определение: плоская кривая, которая в каждой своей

Слайд 16Однопараметрическое семейство плоских кривых (ОСПК)Теорема 1. Огибающая ОСПК, если она существует,

Слайд 17Однопараметрическое семейство плоских кривых (ОСПК)Рассмотрим точку касания некоторой кривой семейства и

Слайд 18, следовательно, огибающая удовлетворяет системеуравнений:тогда огибающая есть дискриминантная кривая. Однопараметрическое семейство

Слайд 192)Пусть - дискриминантная кривая семейства (35)., следовательно, дискриминантная криваякасается в

Слайд 20(35)где а – параметр.

Слайд 21(35)где а – параметр.

Слайд 22(31)

Слайд 23Определение: однопараметрическим

Слайд 24(31)

Слайд 25(31)

Слайд 26(29)(29) – неявное уравнение плоской кривой.

Похожие презентации

Обратная связь

Что такое ThePresentation.ru?

Слайд 1ТЕОРИЯ КРИВЫХ
Плоские кривые

Слайд 2Плоские кривые
Пусть кривая целиком лежит в плоскости xOy.
Кривая задана:

- параметрическое

Слайд 3Плоские кривые
Из (29) выразим y:

(30)
(30) – задание явной функции в виде

Слайд 4Особые точки плоской кривой
Определение: точка
называется особой точкой
плоской кривой, заданной неявным

Слайд 5Классификация особых точек плоской кривой
Обозначим

,
и подставим в уравнение (31):

(33)
продифференцируем по t

Слайд 6Рассмотрим (33) в особой точке:
Классификация особых точек плоской кривой
(34)

:
А.

Уравнение (34’) не

Слайд 7Б.
1)

Уравнение (34’) имеет 2 решения.
Имеет 2 касательные, следовательно, через точку
В.
проходит

Слайд 8Классификация особых точек плоской кривой

Последние две точки не принадлежат кривой, следовательно,
точка

Слайд 10Классификация особых точек плоской кривой
2)
Точка возврата 1-го рода.
В особой точке обе

Слайд 11Классификация особых точек плоской кривой
3)
Точка возврата 2-го рода.
В ней

Слайд 124) Точка самоприкосновения

5)

Классификация особых точек плоской кривой

Слайд 13Однопараметрическое семейство плоских кривых (ОСПК)
Определение: однопараметрическим семейством плоских

Слайд 142)
Однопараметрическое семейство плоских кривых (ОСПК)

Слайд 15Однопараметрическое семейство плоских кривых (ОСПК)
Определение: плоская кривая, которая в каждой своей

Слайд 16Однопараметрическое семейство плоских кривых (ОСПК)
Теорема 1.
Огибающая ОСПК, если она существует,

Слайд 17Однопараметрическое семейство плоских кривых (ОСПК)

Рассмотрим точку касания некоторой кривой семейства

и

Слайд 18

, следовательно, огибающая удовлетворяет системе
уравнений:

тогда огибающая есть дискриминантная кривая.
Однопараметрическое семейство

Слайд 192)
Пусть

- дискриминантная кривая семейства (35).

, следовательно, дискриминантная кривая
касается в

Слайд 20
(35)
где а – параметр.

Слайд 21
(35)
где а – параметр.

Слайд 22
(31)

Слайд 24
(31)

Слайд 25
(31)

Слайд 26

(29)
(29) – неявное уравнение плоской кривой.