Основой всех таких задач служит классическая задача коммивояжера.
Формулировка задачи. Коммивояжер должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, сведя при этом затраты на передвижения к минимуму.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теория графов. Задача коммивояжера презентация
Содержание
- 1. Теория графов. Задача коммивояжера
- 2. ТЕОРИЯ ГРАФОВ ЗАДАЧА КОММИВОЯЖЕРА Взвешенный граф
- 3. ТЕОРИЯ ГРАФОВ ЗАДАЧА КОММИВОЯЖЕРА Графическая модель
- 4. ТЕОРИЯ ГРАФОВ ЗАДАЧА КОММИВОЯЖЕРА Методы решения
- 5. ТЕОРИЯ ГРАФОВ ЗАДАЧА КОММИВОЯЖЕРА Алгоритм «ближайшего
- 6. ТЕОРИЯ ГРАФОВ ЗАДАЧА КОММИВОЯЖЕРА Формулировка алгоритма.
- 7. ТЕОРИЯ ГРАФОВ ЗАДАЧА КОММИВОЯЖЕРА Пример. Применим
- 8. ТЕОРИЯ ГРАФОВ ЗАДАЧА КОММИВОЯЖЕРА Решение.
- 9. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ Существует класс
- 10. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ В любом связном графе
- 11. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ Остовное дерево в графе
- 12. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ Все остовные деревья графа
- 13. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ Рисунок 17
- 14. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ Нахождение минимального остовного дерева
- 15. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ На этом свойстве основан
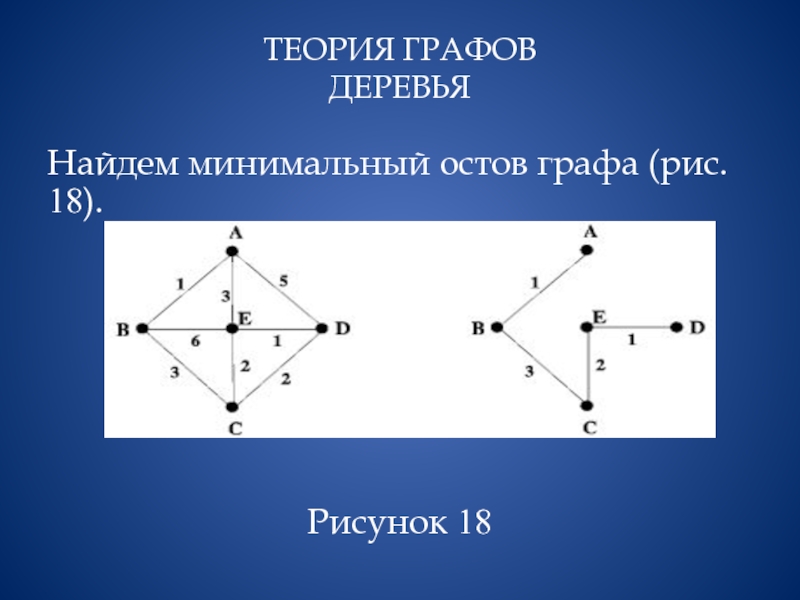
- 16. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ Найдем минимальный остов графа
- 17. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ U={0}, V-U={A,B,C,D,E}. Начнем с
- 18. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ Опять выбираем ребро с
- 19. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ По предложенной взвешенной
- 20. ТЕОРИЯ ГРАФОВ ДЕРЕВЬЯ
Слайд 1ТЕОРИЯ ГРАФОВ
ЗАДАЧА КОММИВОЯЖЕРА
Гамильтоновы графы применяются для моделирования многих практических задач.
Слайд 2ТЕОРИЯ ГРАФОВ
ЗАДАЧА КОММИВОЯЖЕРА
Взвешенный граф – граф, каждому ребру которого поставлено
в соответствие некоторое числовое значение, называемое весом ребра. Элементами матрицы смежности взвешенного графа являются весовые значения ребер (дуг) графа.
Слайд 3ТЕОРИЯ ГРАФОВ
ЗАДАЧА КОММИВОЯЖЕРА
Графическая модель задачи коммивояжера состоит из гамильтонова графа,
вершины которого изображают города, а ребра – связывающие их дороги. Кроме того, каждое ребро оснащено весом, обозначающим транспортные затраты, необходимые для передвижения по соответствующей дороге, такие, как, например, расстояние между городами или время движения по дороге. Для решения задачи необходимо найти гамильтонов цикл минимального общего веса.
Слайд 4ТЕОРИЯ ГРАФОВ
ЗАДАЧА КОММИВОЯЖЕРА
Методы решения задачи коммивояжера:
метод ветвей и границ (алгоритм
Литтла);
алгоритм «ближайшего соседа» («жадный алгоритм»);
метод нахождения минимального остовного дерева («деревянный алгоритм»);
алгоритм Дейкстры.
алгоритм «ближайшего соседа» («жадный алгоритм»);
метод нахождения минимального остовного дерева («деревянный алгоритм»);
алгоритм Дейкстры.
Слайд 5ТЕОРИЯ ГРАФОВ
ЗАДАЧА КОММИВОЯЖЕРА
Алгоритм «ближайшего соседа» относится к алгоритмам поиска субоптимального
решения. Субоптимальное решение необязательно даст цикл минимального oбщегo веса, но найденный цикл будет, как правило, значительно меньшего веса, чем большинство произвольных гамильтоновых циклов.
Слайд 6ТЕОРИЯ ГРАФОВ
ЗАДАЧА КОММИВОЯЖЕРА
Формулировка алгоритма.
Пункты (вершины) обхода графа последовательно включаются в
маршрут, причем, каждый очередной включаемый пункт должен быть ближайшим к последнему выбранному пункту среди всех остальных, ещё не включенных в состав маршрута
Слайд 7ТЕОРИЯ ГРАФОВ
ЗАДАЧА КОММИВОЯЖЕРА
Пример. Применим алгоритм ближайшего соседа к графу, изображенному
на рис. 15. За исходную вершину возьмем вершину D.
Рисунок 15
Рисунок 15
А
В
С
D
6
8
5
3
7
10
Слайд 9
ТЕОРИЯ ГРАФОВ
ДЕРЕВЬЯ
Существует класс графов, называемых деревьями. Дерево – связный граф, не
содержащий циклов (ацикличный граф).
Пусть G = (V, Е) – граф с n вершинами и m ребрами. Можно сформулировать несколько необходимых и достаточных условий, при которых G является деревом:
• любая пара вершин в G соединена единственным путем;
• G связен и m = n-1;
• G связен, а удаление хотя бы одного его ребра нарушает связность графа;
• G ацикличен, но если добавить хотя бы одно ребро, то в G
появится цикл.
Пусть G = (V, Е) – граф с n вершинами и m ребрами. Можно сформулировать несколько необходимых и достаточных условий, при которых G является деревом:
• любая пара вершин в G соединена единственным путем;
• G связен и m = n-1;
• G связен, а удаление хотя бы одного его ребра нарушает связность графа;
• G ацикличен, но если добавить хотя бы одно ребро, то в G
появится цикл.
Слайд 10ТЕОРИЯ ГРАФОВ
ДЕРЕВЬЯ
В любом связном графе найдется подграф, являющийся деревом. Подграф в
G, являющийся деревом и включающий в себя все вершины G, называется остовным деревом.
Слайд 11ТЕОРИЯ ГРАФОВ
ДЕРЕВЬЯ
Остовное дерево в графе G строится просто: выбираем произвольное его
ребро и последовательно добавляем другие ребра, не создавая при этом циклов, до тех пор, пока нельзя будет добавить никакого ребра, не получив при этом цикла.
Для построения остовного дерева в графе из n вершин необходимо выбрать ровно n - 1 ребро.
Для построения остовного дерева в графе из n вершин необходимо выбрать ровно n - 1 ребро.
Слайд 12ТЕОРИЯ ГРАФОВ
ДЕРЕВЬЯ
Все остовные деревья графа (рис. 16), представлены на рисунке 17.
Рисунок
16
Слайд 14ТЕОРИЯ ГРАФОВ
ДЕРЕВЬЯ
Нахождение минимального остовного дерева (minimal spanning tree – MST).
В графе
G=(V, E) рассмотрим U – некоторое подмножество V, такое что U і V-U не пусты. Пусть (u, v) – ребро наименьшей стоимости, одна вершина которого – u принадлежит U, а другая – v принадлежит V-U. Тогда существует некоторое MST, которое содержит ребро (u, v).
Слайд 15ТЕОРИЯ ГРАФОВ
ДЕРЕВЬЯ
На этом свойстве основан алгоритм Прима.
Начинаем с пустого U=0. Добавляем
к U вершины, каждый раз находя ребро наименьшей стоимости между U и V-U. Перебрав все вершины, находим минимальный остов.
Слайд 17ТЕОРИЯ ГРАФОВ
ДЕРЕВЬЯ
U={0}, V-U={A,B,C,D,E}.
Начнем с вершины В: U={B}, V-U={A,C,D,E}.
Выбираем ребро с наименьшим
весом – это ребро ВА (вес – 1): U={B,A}, V-U={C,D,E}.
Теперь выбираем ребро с наименьшим весом к оставшимся вершинам, т.е. из V-U ={C,D,E}.
Если вес ребер одинаковый – выбираем любое, например ребро ВС (вес ребра – 3): U={B,A,C}, V-U={D,E}.
Теперь выбираем ребро с наименьшим весом к оставшимся вершинам, т.е. из V-U ={C,D,E}.
Если вес ребер одинаковый – выбираем любое, например ребро ВС (вес ребра – 3): U={B,A,C}, V-U={D,E}.
Слайд 18ТЕОРИЯ ГРАФОВ
ДЕРЕВЬЯ
Опять выбираем ребро с наименьшим весом к оставшимся вершинам, т.е.
из V-U ={D,E}, например, ребро СЕ (вес ребра – 2): U={B,A,C,Е}, V-U={D}. Остается ребро ED: U={B,A,C,Е,D}, V-U={0}.
Слайд 19ТЕОРИЯ ГРАФОВ
ДЕРЕВЬЯ
По предложенной взвешенной матрице смежности восстановить граф и найти
его все возможные минимальные остовные деревья.