- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Теорема Виета презентация
Содержание
- 1. Теорема Виета
- 2. Классификация видов квадратных уравнений Квадратные уравнения
- 3. Обратим внимание Ещё одно интересное соотношение – дискриминант уравнения равен квадрату разности его корней: D=(x1-x2)2.
- 4. Франсуа Виет (1540–1603) родился во Франции. Разработал
- 5. Теорема Виета Искусство,
- 6. Приведённое квадратное уравнение. Квадратное уравнение вида
- 7. Теорема Виета. Если приведённое
- 8. Теорема, обратная теореме Виета Если для чисел
- 9. Пусть ax2+bx+c=0 квадратное уравнение общего вида
- 10. Прямая теорема: Если х₁ и х₂
- 11. МОУ СОШ с.Кувак-Никольское учитель Никулкина О.А. Применение
- 12. 1. Если произведение и сумма корней –
- 13. 5 6
- 14. a>0,c0-2 различных корня 1 -6 3
- 15. Решите уравнения
- 16. Найдите для каждого уравнения соответствующие корни, пользуясь
- 17. Определите корни квадратного уравнения, пользуясь теоремой, обратной
- 18. Пусть
- 19. Окончен урок, и выполнен план. Спасибо, ребята,
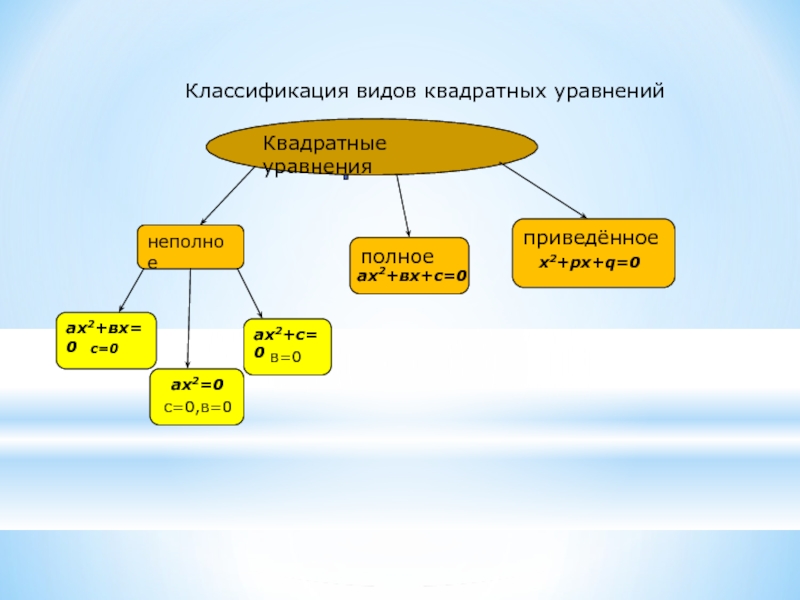
Слайд 2Классификация видов квадратных уравнений
Квадратные уравнения
неполное
полное
приведённое
ах2+вх=0
ах2=0
ах2+с=0
с=0
с=0,в=0
в=0
ах2+вх+с=0
х2+pх+q=0
Слайд 3Обратим внимание
Ещё одно интересное соотношение – дискриминант уравнения равен квадрату разности
D=(x1-x2)2.
Слайд 4Франсуа Виет (1540–1603) родился во Франции. Разработал почти всю элементарную алгебру;
Теорема Виета
Слайд 5Теорема
Виета
Искусство, которое я излагаю, ново…Все математики знали,
Франсуа Виет.
Слайд 6Приведённое квадратное уравнение.
Квадратное уравнение вида
называется приведённым (а=1).
Квадратное уравнение
где
Слайд 7Теорема Виета.
Если приведённое квадратное уравнение х2+px+q=0 имеет неотрицательный
х1+х2=-p,
х1·х2=q
Слайд 8Теорема, обратная теореме Виета
Если для чисел х1, х2, p, q
справедливы формулы
уравнения
х1+х2=-p,
х1·х2=q
х2+px+q=0
Слайд 9Пусть ax2+bx+c=0 квадратное уравнение общего вида
Теорема
Если квадратное уравнение общего вида имеет неотрицательный дискриминант и если
уравнения, то
х1 и х2 – корни
х1 +х2=-b/a
х1 ·х2= c/a
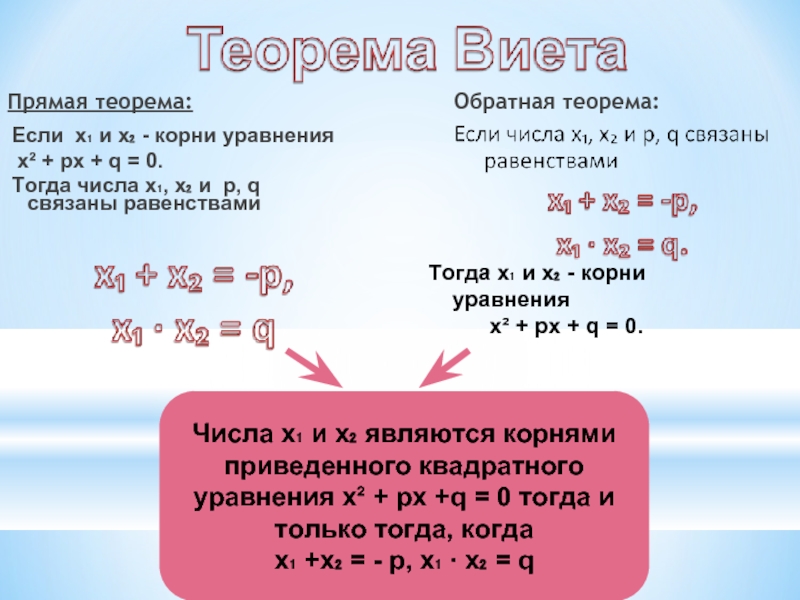
Слайд 10Прямая теорема:
Если х₁ и х₂ - корни уравнения
х² + px
Тогда числа х₁, х₂ и p, q связаны равенствами
Обратная теорема:
Тогда х₁ и х₂ - корни уравнения
х² + px + q = 0.
Числа х₁ и х₂ являются корнями приведенного квадратного уравнения х² + px +q = 0 тогда и только тогда, когда
x₁ +х₂ = - p, x₁ ∙ x₂ = q
Слайд 11МОУ СОШ с.Кувак-Никольское учитель Никулкина О.А.
Применение теоремы Виета
Найдите сумму и произведение
-41
-371
210
15
6
0
-16
-11
Слайд 121. Если произведение и сумма корней – положительные, то оба корня
Слайд 13
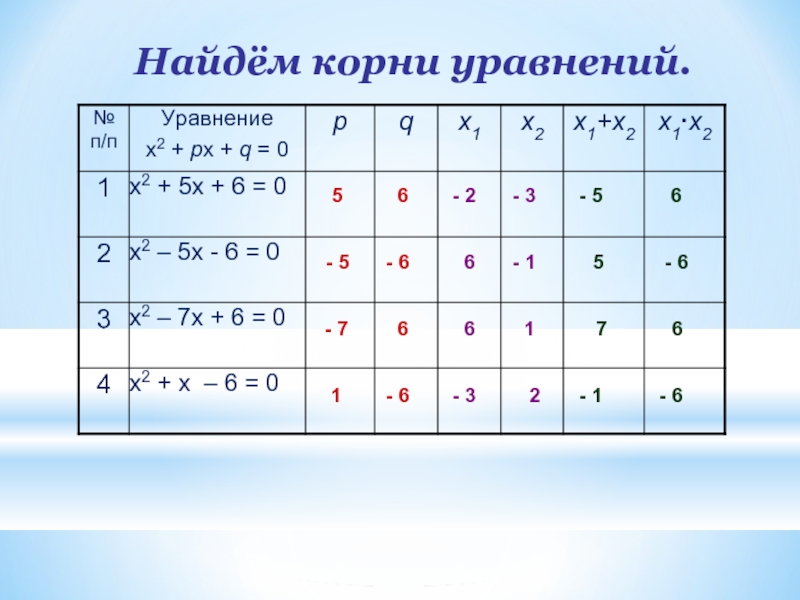
5
6
- 5
- 6
- 5
5
- 6
- 7
6
7
6
- 6
- 6
1
- 1
Найдём корни уравнений.
- 2
- 3
6
- 1
6
1
- 3
2
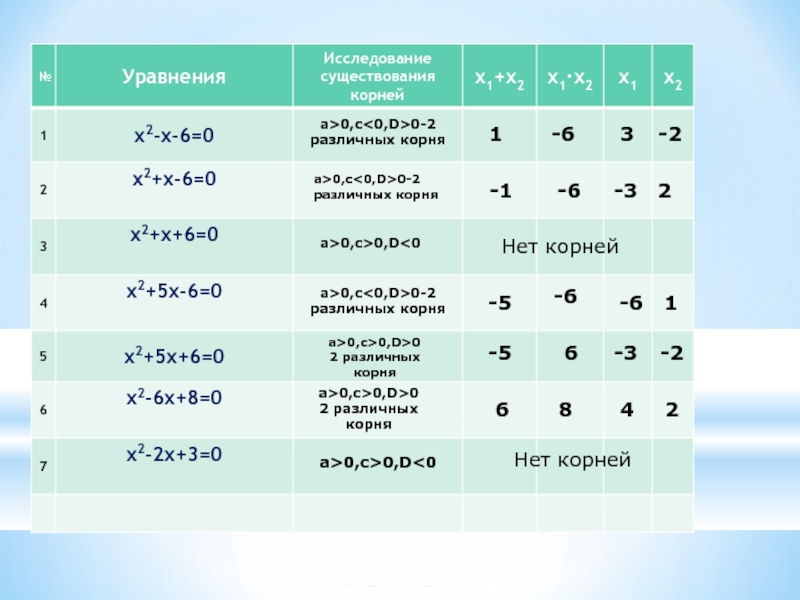
Слайд 14a>0,c0-2 различных корня
1
-6
3
-2
a>0,c0-2 различных корня
-1
-6
-3
2
a>0,c>0,D0,c0-2 различных корня
-5
-6
-6
1
a>0,c>0,D>0
2
-5
6
-3
-2
a>0,c>0,D>0
2 различных корня
6
8
4
2
a>0,c>0,D<0
Нет корней
Слайд 16Найдите для каждого уравнения соответствующие корни, пользуясь теоремой Виета:
а) x2 -
b) x2 - 7x + 10=0 x 1 = -5 x2 = -5
c) x2 + 12x + 32=0 x 1 = 5 x2 = 2
d) x2 + 3x - 18=0 x 1 = -6 x2 = 3
e) x2 + 10x + 25=0 x 1 = - 4 x2 = - 8
Слайд 17Определите корни квадратного уравнения, пользуясь теоремой, обратной теореме Виета:
Х1 =-12, х2 =1
х1 =16, х2 =-1
х1 =3, х2 =-2
х1 =6, х2 =2
х1 =-6, х2 =-1
Слайд 18Пусть ,
При каком значении q уравнение
имеет корни, один из которых в 2 раза больше другого?
Решение:
По теореме, обратной теореме Виета:
Ответ: при q = 8.
Задача:
Слайд 19Окончен урок, и выполнен план.
Спасибо, ребята, огромное вам.
За то, что упорно
И знания точно уж вам пригодились.