- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тела вращения Цилиндр. Конус. Шар. Сфера презентация
Содержание
- 1. Тела вращения Цилиндр. Конус. Шар. Сфера
- 2. Определение цилиндра как геометрического тела Цилиндром
- 3. Круги называются основаниями цилиндра Отрезки, соединяющие
- 4. Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований.
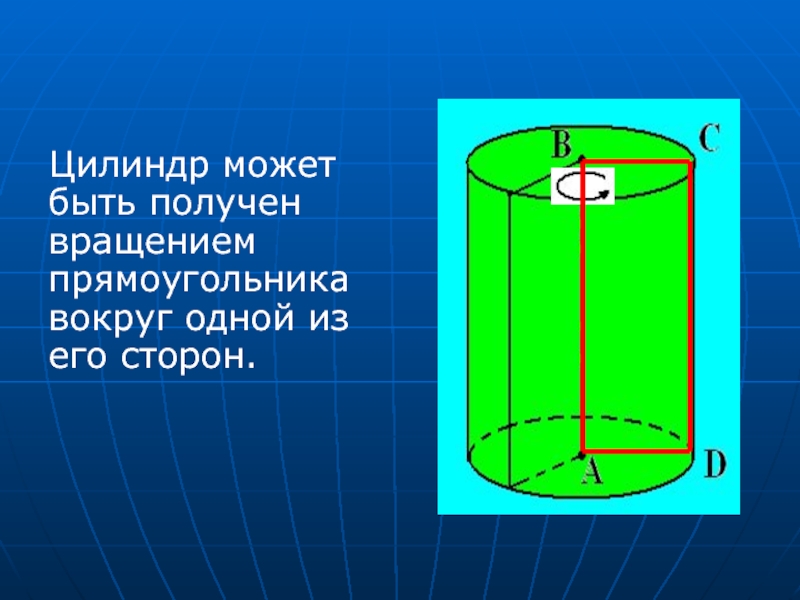
- 5. Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.
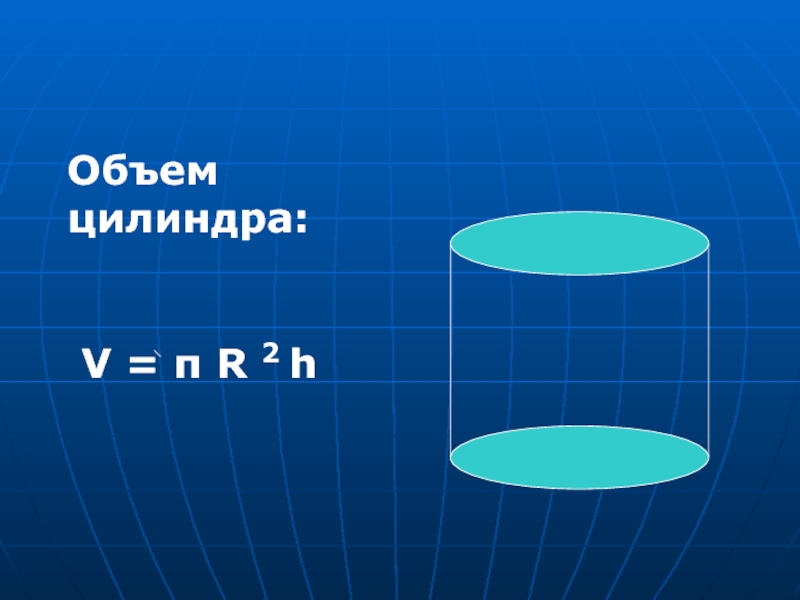
- 6. Объем цилиндра:
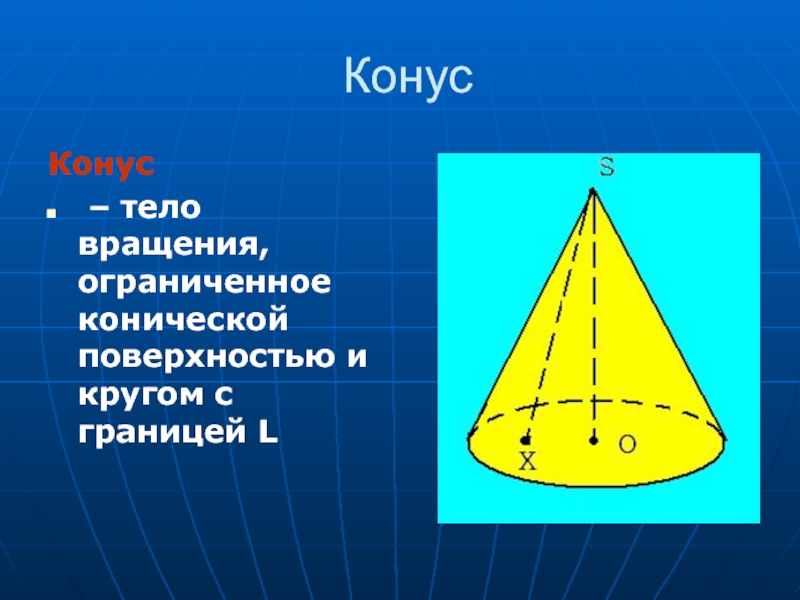
- 7. Конус Конус –
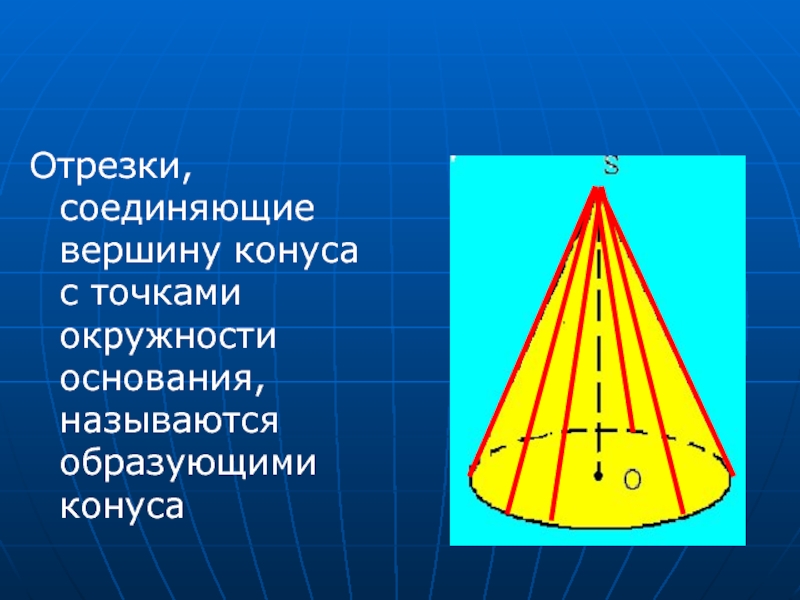
- 8. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса
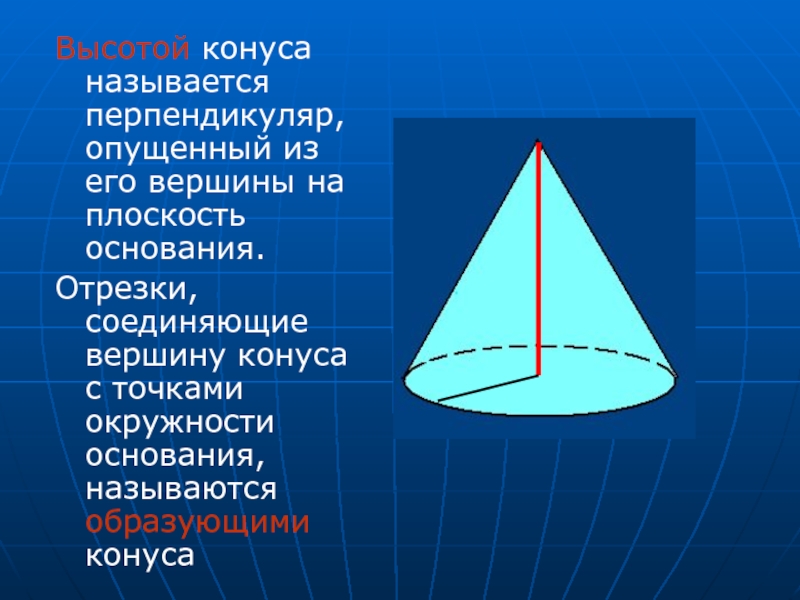
- 9. Высотой конуса называется перпендикуляр, опущенный из его
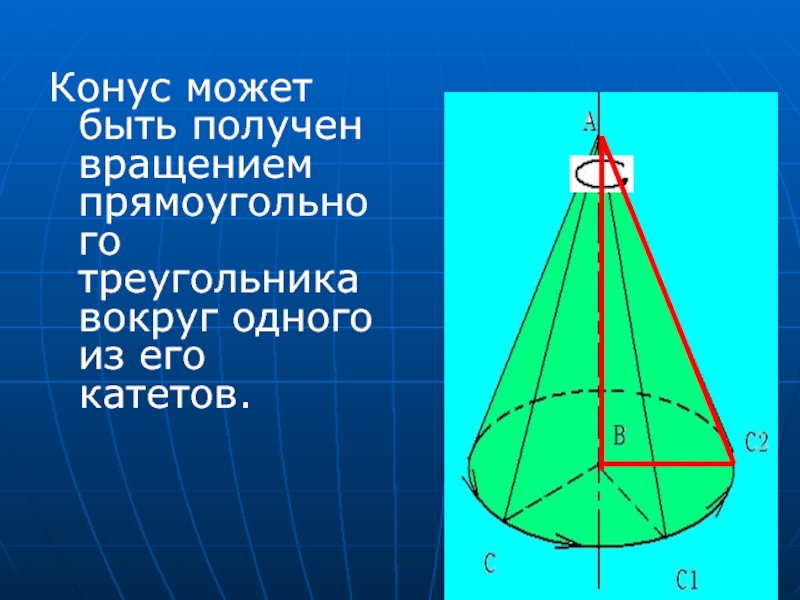
- 10. Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.
- 11. Усеченный конус Плоскость, параллельная основанию конуса и
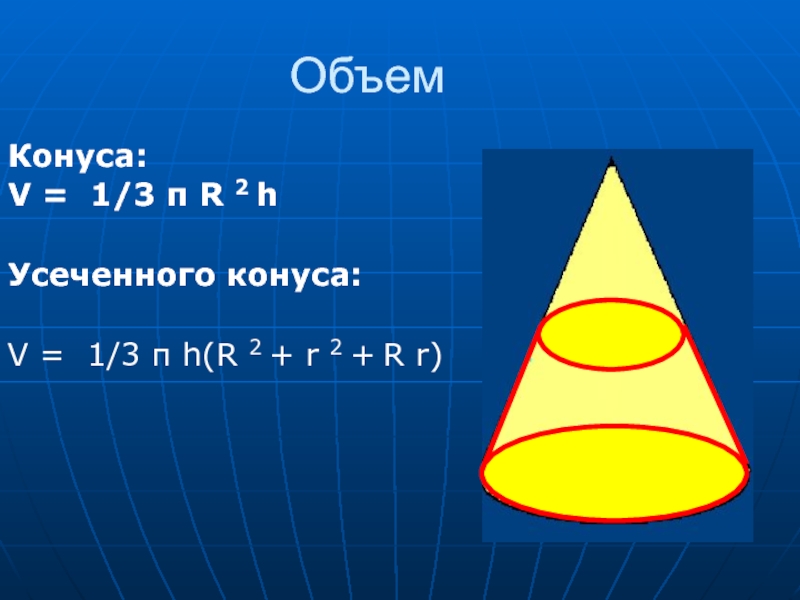
- 12. Объем Конуса: V = 1/3 π R
- 13. Шар Шаром называется тело, которое
- 14. Любой отрезок, соединяющий центр шара с точкой
- 15. Граница шара называется сферой.
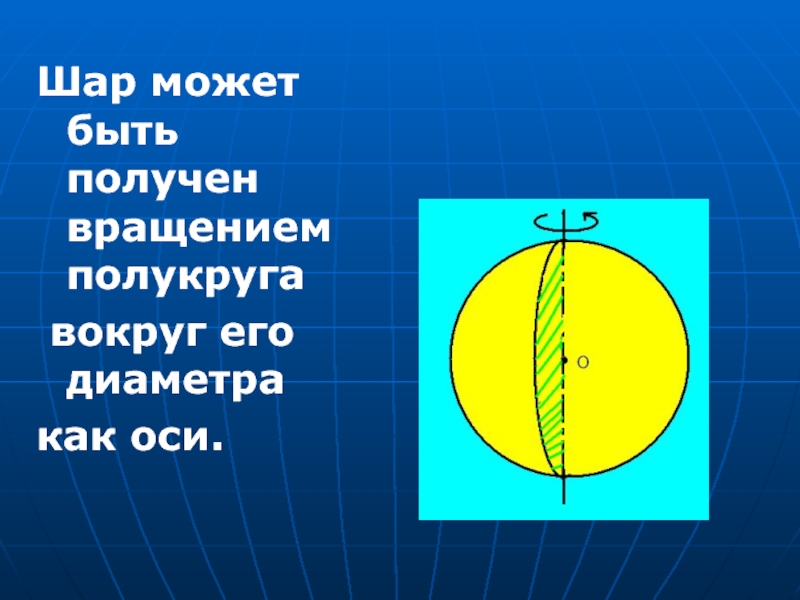
- 16. Шар может быть получен вращением полукруга вокруг его диаметра как оси.
- 17. Объем шара вычисляется по
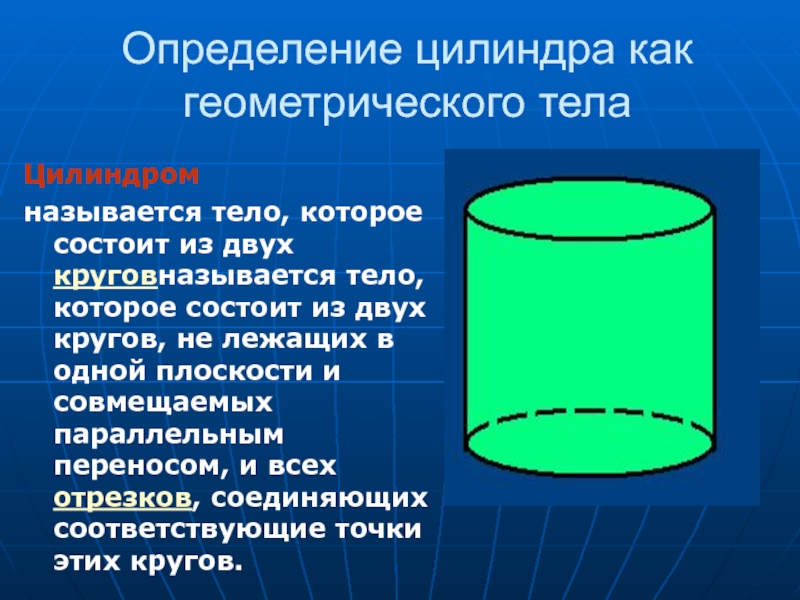
Слайд 2Определение цилиндра как геометрического тела
Цилиндром
называется тело, которое состоит из двух
круговназывается тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
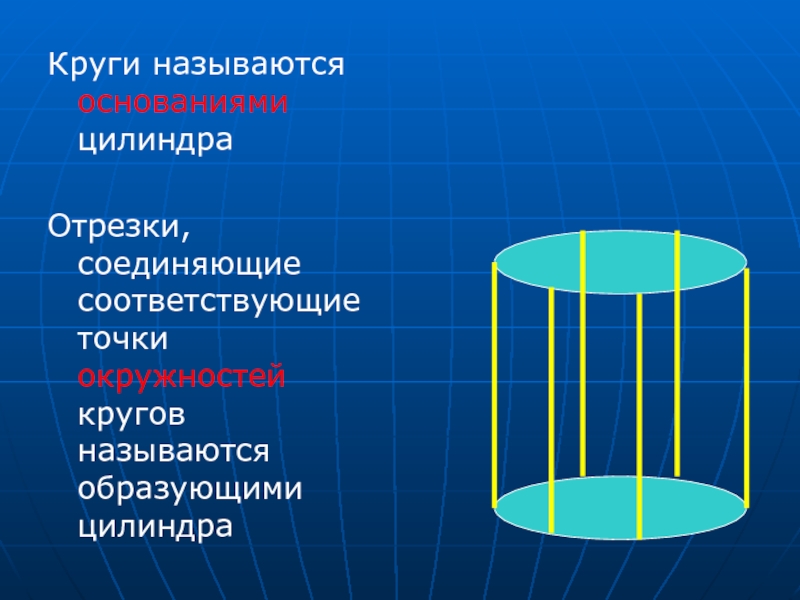
Слайд 3Круги называются основаниями цилиндра
Отрезки, соединяющие соответствующие точки окружностей кругов называются образующими
цилиндра
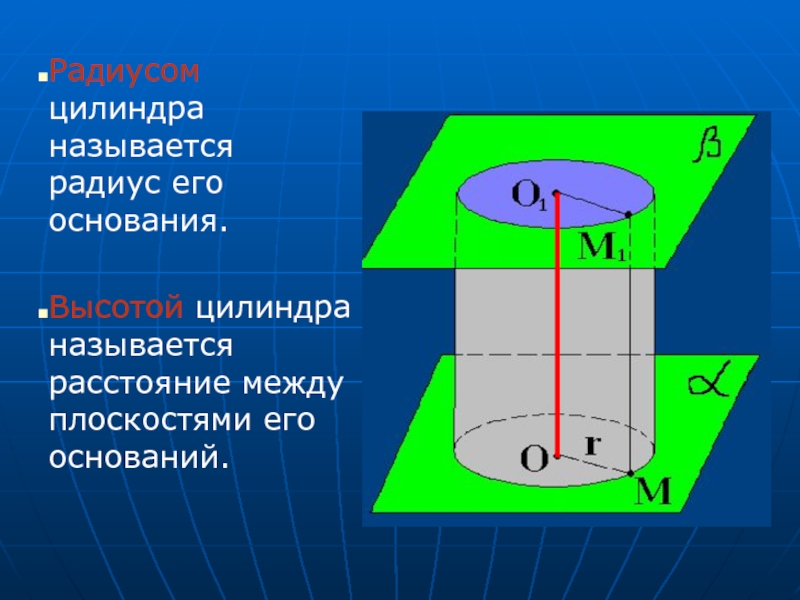
Слайд 4Радиусом цилиндра называется радиус его основания.
Высотой цилиндра называется расстояние между плоскостями
его оснований.
Слайд 8Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса
Слайд 9Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса
Слайд 10Конус может быть получен вращением прямоугольного треугольника вокруг одного из его
катетов.
Слайд 11Усеченный конус
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него
меньший конус.
Оставшаяся часть называется усеченным конусом.
Оставшаяся часть называется усеченным конусом.
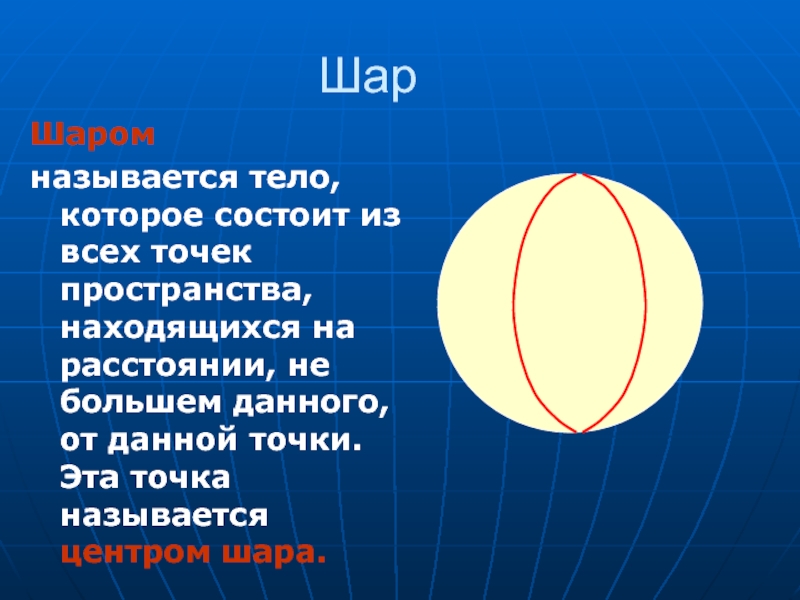
Слайд 13Шар
Шаром
называется тело, которое состоит из всех точек пространства, находящихся
на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара.
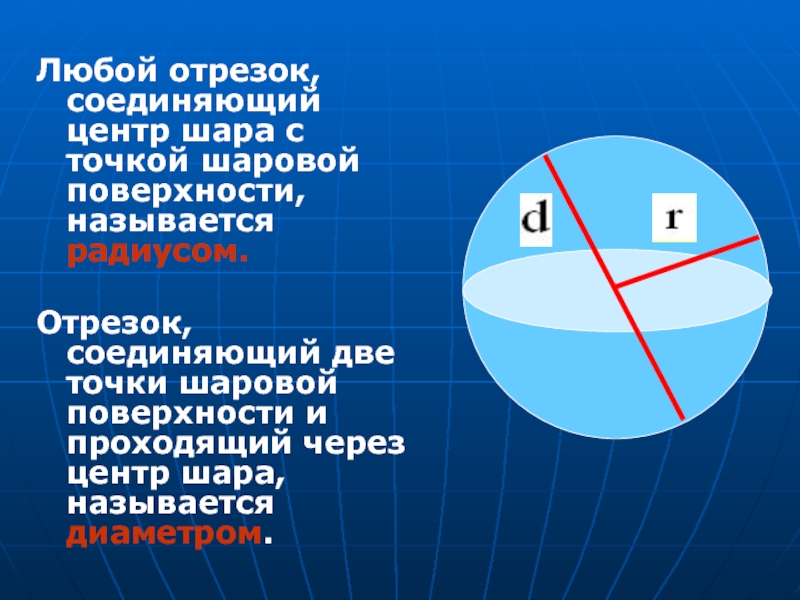
Слайд 14Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, называется радиусом.
Отрезок,
соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром.