- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Связность графов презентация
Содержание
- 1. Связность графов
- 2. 2.1. Маршруты, цепи, циклы
- 3. Маршруты
- 4. Цепи и циклы
- 5. Лемма. Всякий маршрут графа содержит хотя бы
- 6. Пример Маршрут a 1 b 2 c
- 7. Если маршрут рассматривать с учетом ориентации ребер
- 9. Существование маршрутов Рассматривается неориентированный (маршрут не предполагает
- 10. и вершины xk и xj смежны. Для маршрутов других видов задаются соответствующие матрицы смежности.
- 11. Нахождение маршрутов Зададим граф общего вида тройками
- 12. Число маршрутов
- 13. Число различных маршрутов длины 2 из
- 14. Пример Для орграфов изменяется только матрица R.
- 15. c
- 16. Достижимость
- 17. Ориентированные маршруты Понятие маршрута можно обобщить на
- 18. 2.2. Компоненты связности
- 19. Компоненты и бикомпоненты
- 20. Отношение «быть в одной компоненте »
- 21.
- 22. Для ориентированных графов
- 23. Множество вершин, достижимых из вершины x, обозначим
- 24.
- 25. Алгоритм работает «на месте» -- матрица Rl+1 записывается на месте матрицы R.
- 26. Фрагмент программы выглядит так: Пример (для компонент) (**)
- 27.
- 28. 1 2 3 5 4 Пример (бикомпоненты, матрица достижимости)
- 29. Фрагмент программы: for k=1 to
- 30. Ахо А., Хопкрофт Д., Ульман Д.
- 31. Пример (алгоритм Уоршалла)
- 32. Warshall Stephen (1935 – 2006) https://en.wikipedia.org/wiki/Stephen_Warshall Warshall
- 33. 2.3. Кратчайшие цепи
- 34. Волновой алгоритм
- 35.
- 36. 0 1 2 3 3 4 4
- 38. https://www.youtube.com/watch?v=YDX-ohCVtxY
- 39. 1 1 1 1 1 1 1
- 40. Взвешенный граф
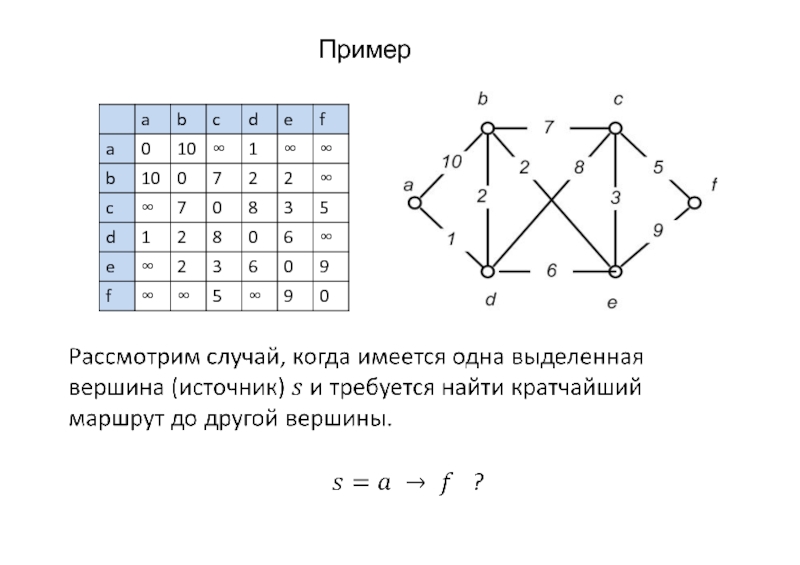
- 41. Пример
- 42. Алгоритм Беллмана - Форда
- 43.
- 44.
- 45. +
- 46. 0a ∞b ∞c 10
- 47. Если
- 48. В таком представлении алгоритм Беллмана — Форда
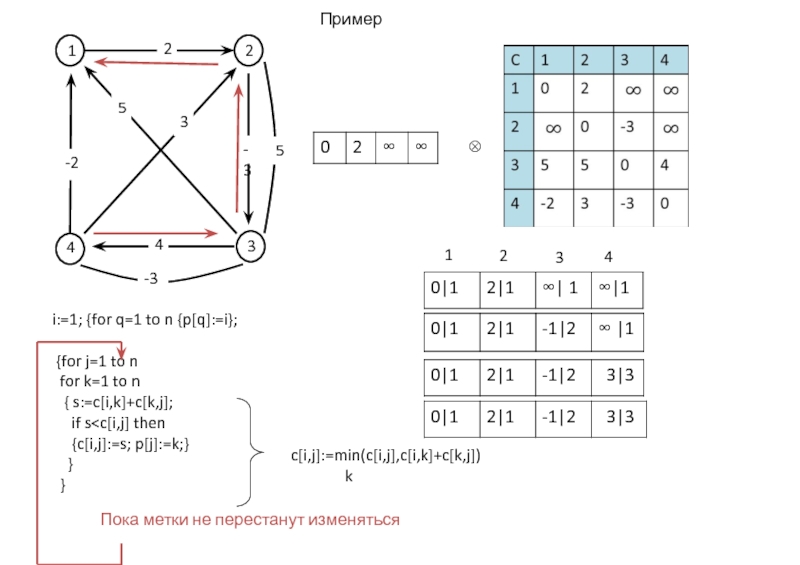
- 49. Пример 1 2 3 4 ⊗
- 50. БЕЛЛМАН, Ричард (1920- 1984) – «отец «динамического
- 51. Алгоритм Дейкстры
- 52.
- 53.
- 54. 0a ∞b ∞c ∞d ∞e ∞f 10a
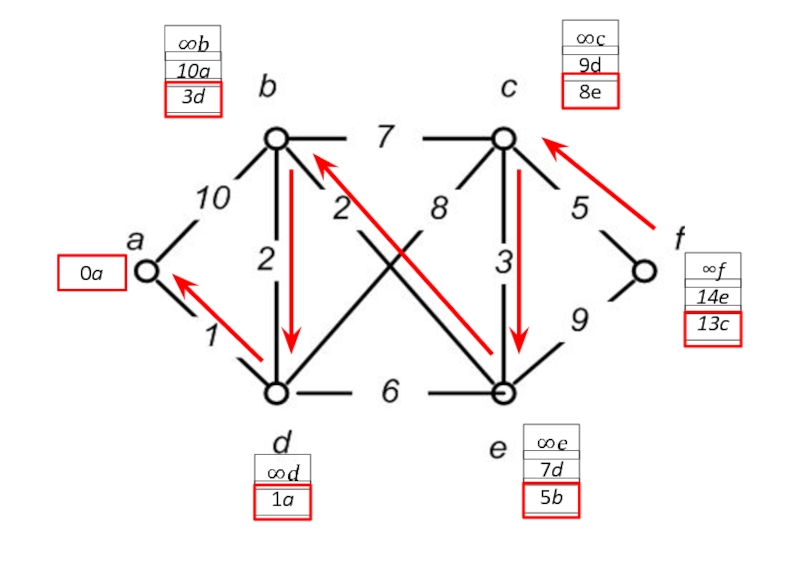
- 55. Иллюстрация работы алгоритма Дейкстры
- 56. Обобщения 1. Алгоритмы Беллмана – Форда и
- 57. ДЕЙКСТРА, Эдсгер (Edsger Dijkstra; 1930-2002). Нидерландский учёный,
- 58. Алгоритм Флойда Замечание. В алгоритме Флойда,
- 59. for i=1 to n
- 60. Фрагмент программы: for k=1 to
- 61. 4 4
- 62. 4 4
- 63. -1 4 4
- 64. Замечание. Алгоритмы Беллмана – Форда и
- 65. ФЛОЙД, Роберт В (Robert W Floyd, 1936 –
Слайд 5Лемма. Всякий маршрут графа содержит хотя бы одну простую цепь, соединяющую
Доказательство
Если в полученном маршруте есть еще повторяющиеся вер-шины, то снова заменяем его более коротким и так далее, пока не выделим маршрут без повторяющихся вершин.
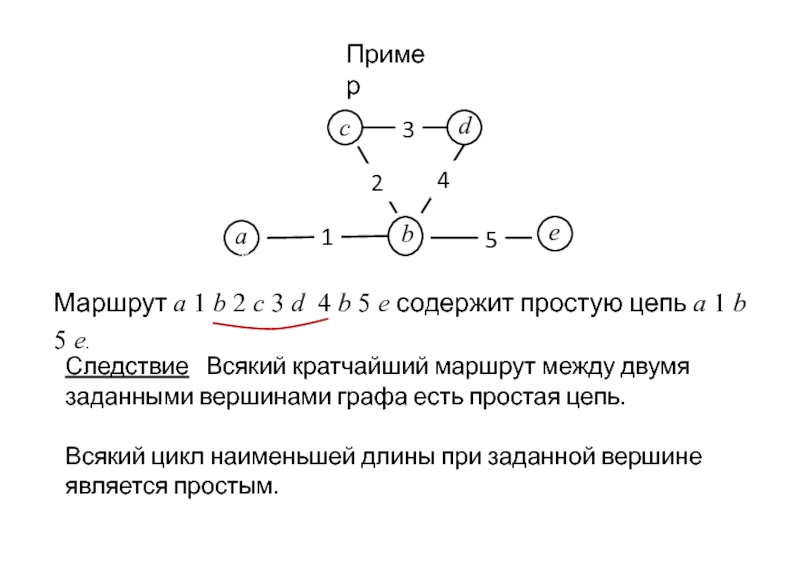
Слайд 6Пример
Маршрут a 1 b 2 c 3 d 4 b 5
Следствие Всякий кратчайший маршрут между двумя заданными вершинами графа есть простая цепь.
Всякий цикл наименьшей длины при заданной вершине является простым.
Слайд 7Если маршрут рассматривать с учетом ориентации ребер (может быть и по
ориентированный маршрут (ормаршрут);
ориентированная цепь (орцепь) – путь;
простая орцепь – простой путь.
Слайд 8
В теории рассматривается ряд задач и алгоритмов определения свойств маршрутов:
существование маршрутов заданной длины;
достижимость вершин;
число маршрутов заданной длины;
компоненты связности и бисвязности;
кратчайшие цепи/пути;
кратчайшие цепи/пути на взвешенных графах.
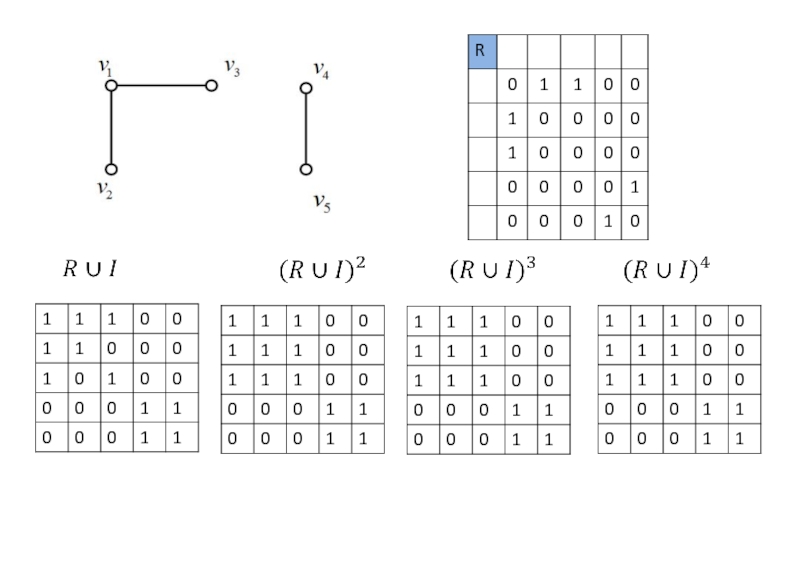
Слайд 9Существование маршрутов
Рассматривается неориентированный (маршрут не предполагает ориентации) униграф (важен лишь факт
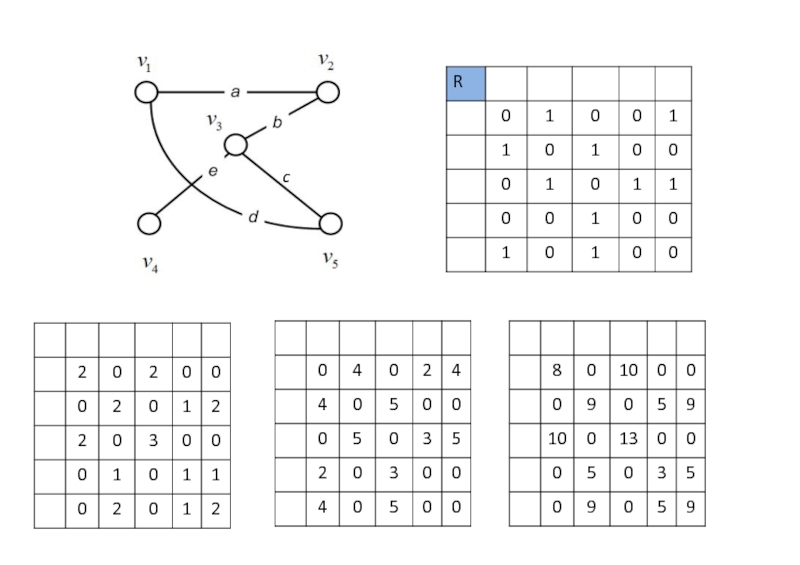
Такой граф можно рассматривать как симметричное бинарное отношение и его можно задать матрицей смежности R, элементы rij которой – булевы. rij=1, если вершины смежны; из вершины xi существует маршрут длины 1 в вершину xj.
Элемент матрицы R2
определяет существование
маршрута длины 2 между этими вершинами. Далее по индукции:
(*)
Слайд 10и вершины xk и xj смежны.
Для маршрутов других видов задаются соответствующие
Слайд 11Нахождение маршрутов
Зададим граф общего вида тройками вида (x,v,y), где x,y∈V, v
Умножение отношений примет следующий вид: если существует
маршрут из вершины xi в вершину xk длины l-1 и есть ребро (xk, v, xj),
то оно добавляется к маршруту длины l.
Длина 1
a1a
a2b
b2a
b3c
b4c
c3b
c4b
Длина 2
a1a1a
a1a2b
a2b2a
a2b3c
a2b4c
b2a1a
b2a2b
b3c3b
…
Длина 3
Слайд 13
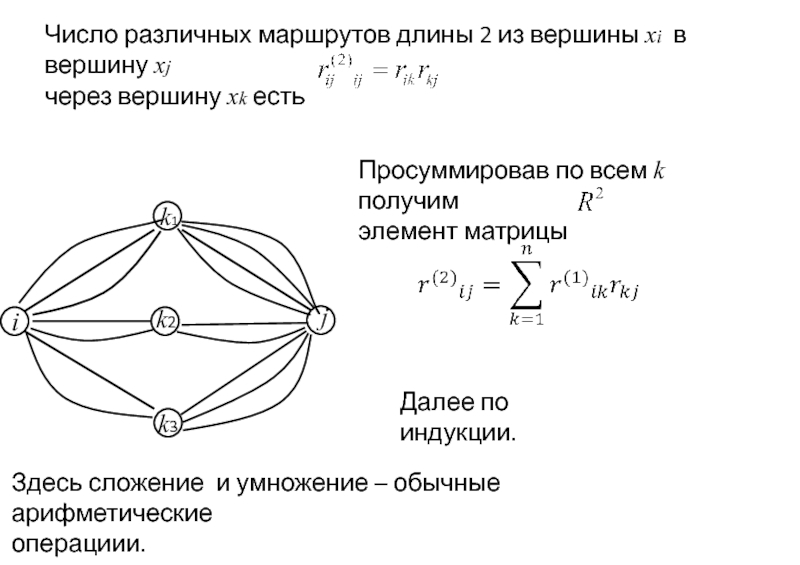
Число различных маршрутов длины 2 из вершины xi в вершину xj
через вершину xk есть
Далее по индукции.
Здесь сложение и умножение – обычные арифметические
операциии.
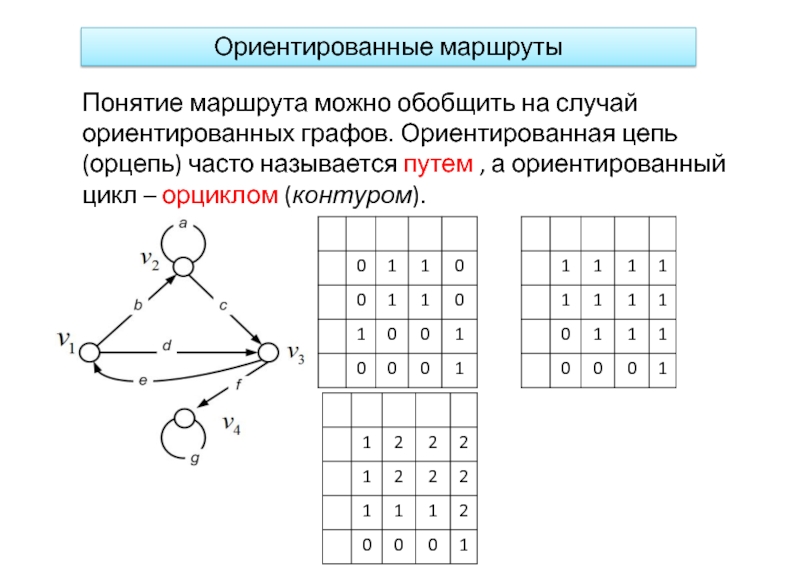
Слайд 17Ориентированные маршруты
Понятие маршрута можно обобщить на случай ориентированных графов. Ориентированная цепь
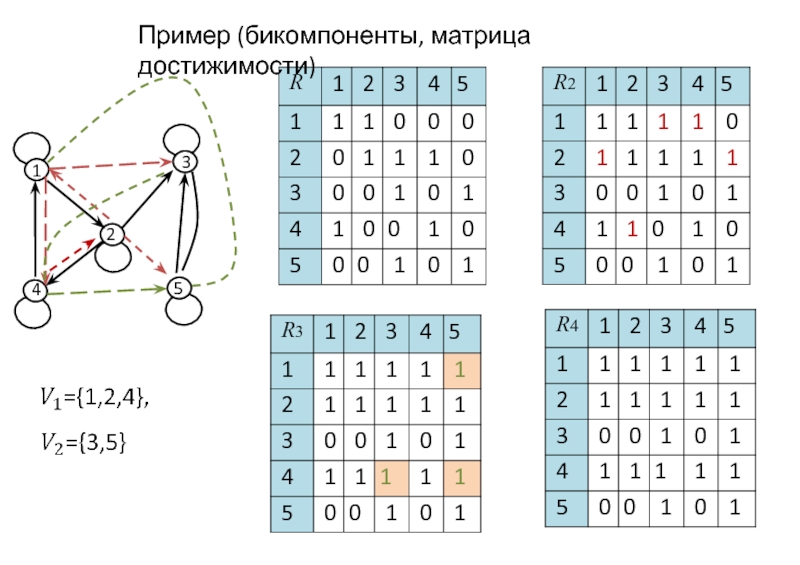
Слайд 23Множество вершин, достижимых из вершины x, обозначим Д(x).
Теорема Вершины x и
тогда, когда Д(x) = Д(y).
⇒ Если x и y взаимодостижимы, то для любой вершины z∈V
ввиду транзитивности отношения взаимодостижимости,
из z∈ Д(x) следует z ∈Д(y), а из z ∈Д(y) следует z∈Д(x),
Поэтому Д(x) = Д(y).
⇐ Пусть Д(x) = Д(y). Так как x∈ Д(x) и y ∈Д(y), то из равенства
Д(x) = Д(y) следует, что y ∈Д(x) и x∈ Д(y), т.е. вершины x и y
взаимодостижимы.
Слайд 29
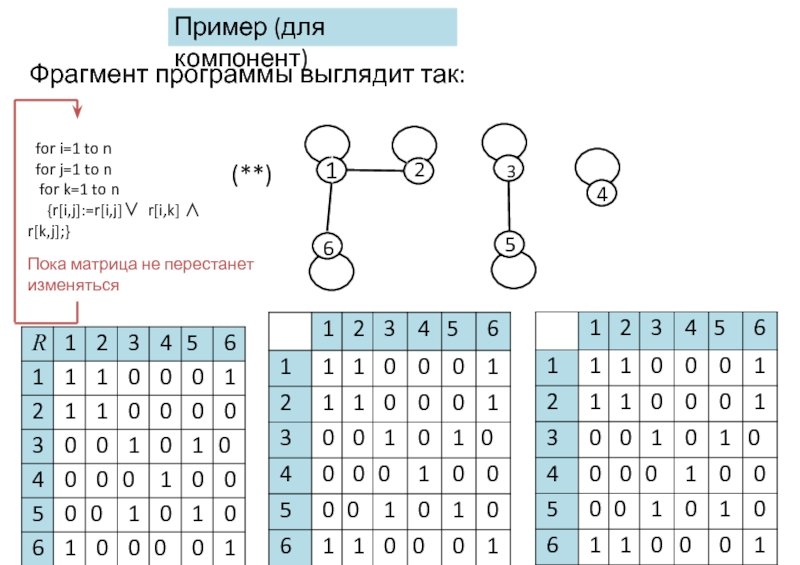
Фрагмент программы:
for k=1 to n
for i=1 to n
for j=1 to n
{r[i,j]:=r[i,j]∨r[i,k] ∧ r[k,j];}
Слайд 30
Ахо А., Хопкрофт Д., Ульман Д. (стр. 194-195)
Структуры данных и алгоритмы.
дательский дом "Вильямс", 2000. — 384 с.
Алгоритм работает «на месте» -- матрица Rk записывается на месте матрицы R.
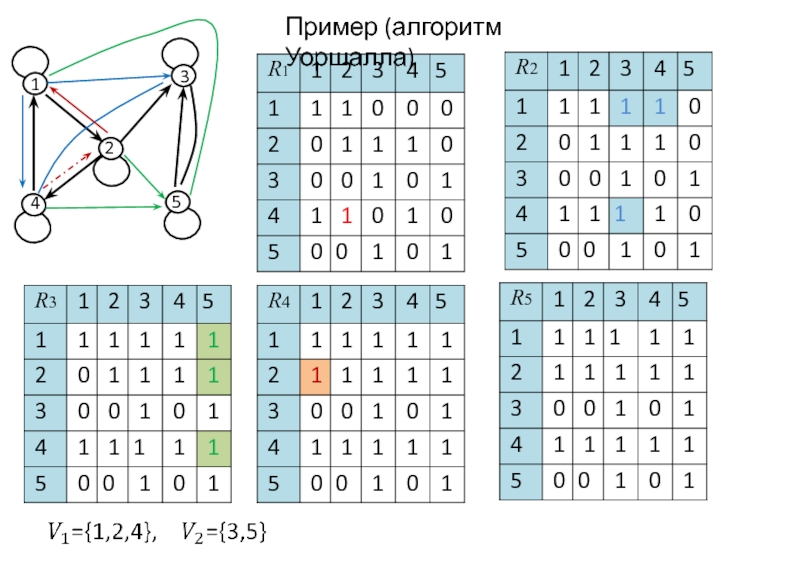
Слайд 32Warshall Stephen (1935 – 2006)
https://en.wikipedia.org/wiki/Stephen_Warshall
Warshall carried out research and development in
Known for Floyd–Warshall algorithm
Слайд 360
1
2
3
3
4
4
5
6
7
Пример 1. Задача о Волке, Козе (Кз) и Капусте (Кп), которых
Вершины графа соответствуют наличию персонажей на исходном берегу. Показаны только допустимые комбинации.
Слайд 391
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
2
2
2
2
2
3
3
3
3
3
3
3
3
3
3
4
4
4
4
4
4
4
4
4
4
4
4
4
4
5
5
5
5
5
5
5
5
5
5
6
6
6
6
6
6
6
6
6
6
6
6
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
7
8
8
8
0
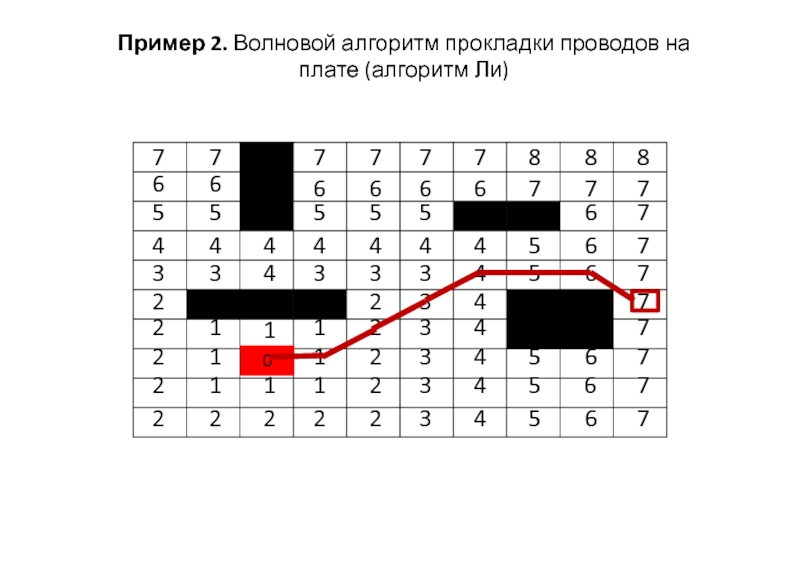
Пример 2. Волновой алгоритм прокладки проводов на плате (алгоритм Ли)
Слайд 47
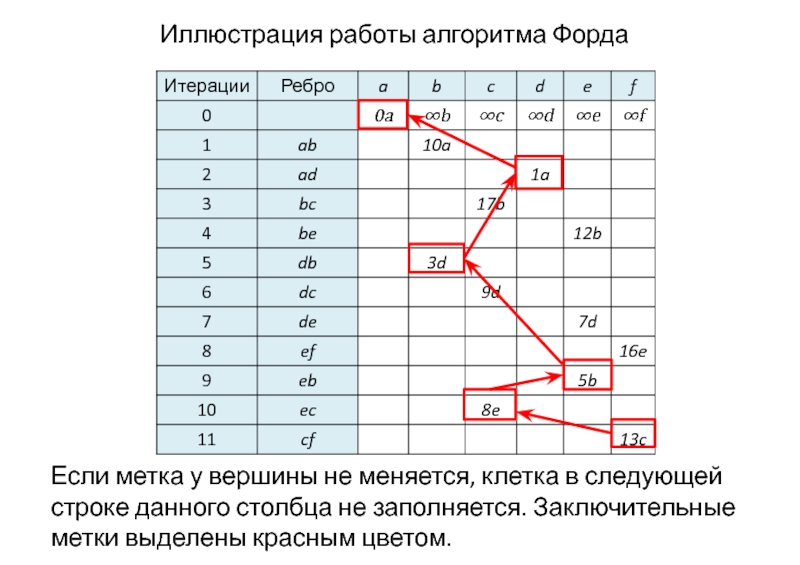
Если метка у вершины не меняется, клетка в следующей строке данного
Иллюстрация работы алгоритма Форда
Слайд 48В таком представлении алгоритм Беллмана — Форда более пригоден
для «ручного» исполнения.
Пусть вершины пронумерованы V={1,2,…,n} и начальная вершина
s =1. Метка вершины L(x)=[l(x),p(x)], где l(x) – метка расстояния
i
j
k
Для нахождения кратчайших цепей/путей между всеми парами вер-шин нужно выполнить цикл по i.
Слайд 50БЕЛЛМАН, Ричард (1920- 1984) – «отец «динамического программирования» - американский математик.
В расцвете творческой жизни после удаления опухоли на позвоночнике 11 лет был прикован к инвалидному креслу, но сохранил полную работоспособность .
ФОРД, Лестер младший (1927 - 2017) – американский математик. Независимо от Беллмана в 1956 г. предложил алгоритм нахождения кратчайшего пути в графе, вместе с Фалкерсоном доказал теорему о наибольшем потоке в сети.
Слайд 56Обобщения
1. Алгоритмы Беллмана – Форда и Дейкстры легко распространяются на случай
2. В алгоритме Беллмана – Форда допускаются отрицательные веса ребер, такие постановки задачи иногда полезны в приложениях. Этим он принципиально отличается от алгоритма Дейкстры, где отрицательные веса невозможны. Но «всеядность» алгоритма Беллмана – Форда оплачивается его более высокой трудоемкостью.
Слайд 57ДЕЙКСТРА, Эдсгер (Edsger Dijkstra; 1930-2002). Нидерландский учёный, труды которого оказали большое
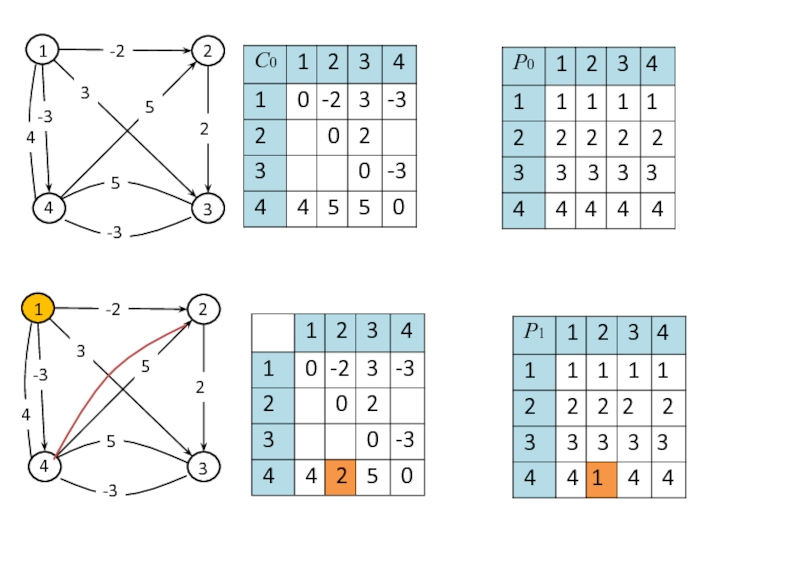
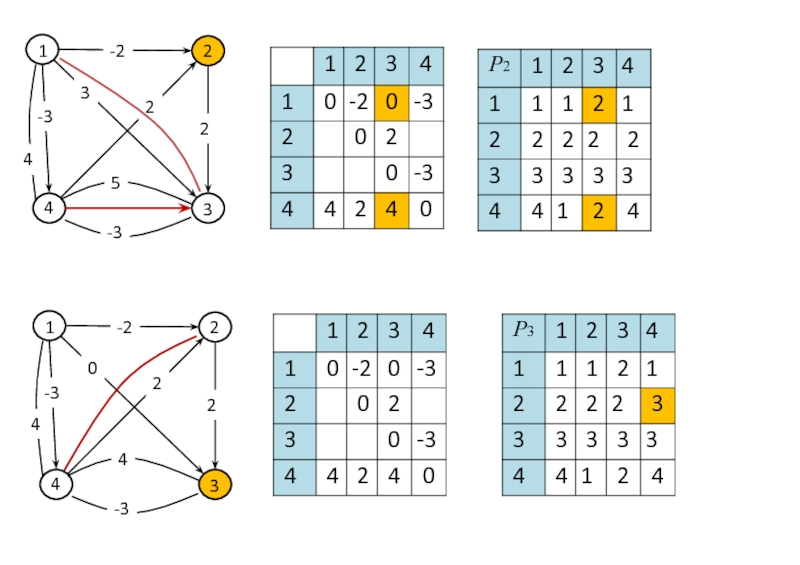
Слайд 58Алгоритм Флойда
Замечание. В алгоритме Флойда, так же как и в алгоритме
Слайд 59
for i=1 to n
for j=1 to n
p[i,j]:=i;
Инициализация
Основной цикл
Алгоритм работает «на месте»:
C и P заменяются на новые; по завершению цикла по k (k=n)
C становится матрицей длин кратчайших цепей/путей, а P -- матрицей
самих цепей/путей.
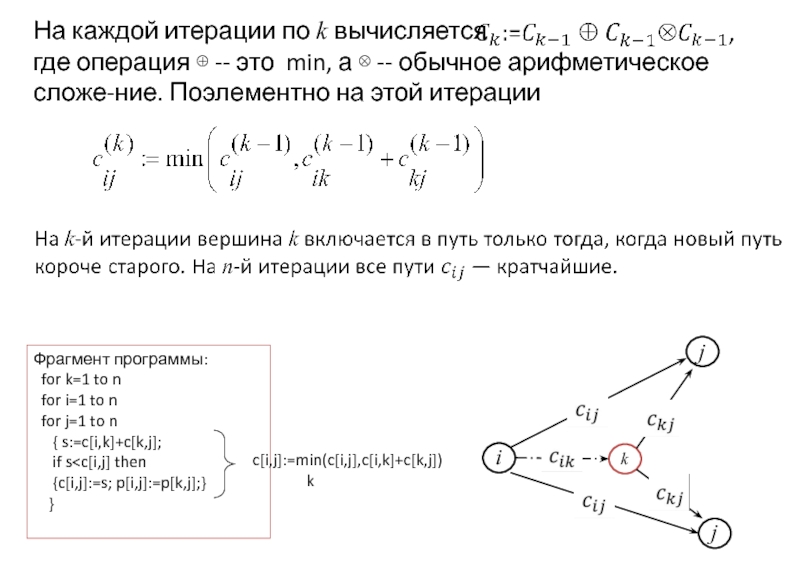
Слайд 60Фрагмент программы:
for k=1 to n
for i=1 to n
for j=1 to n
{ s:=c[i,k]+c[k,j];
if s
}
c[i,j]:=min(c[i,j],c[i,k]+c[k,j])
k
На каждой итерации по k вычисляется
где операция ⊕ -- это min, а ⊗ -- обычное арифметическое сложе-ние. Поэлементно на этой итерации
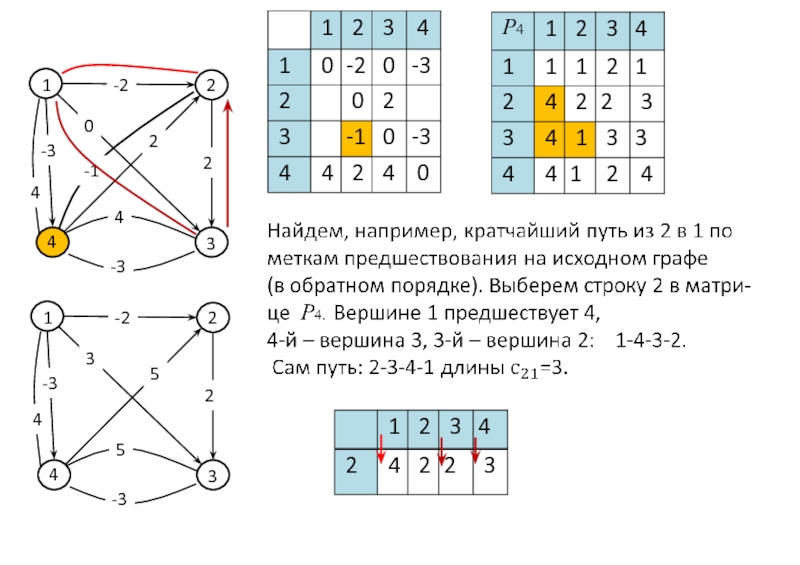
Слайд 64
Замечание. Алгоритмы Беллмана – Форда и Флойда работают кор-
ректно, если в
которых отрицательна). В противном случае длина кратчайшей цепи/
пути уменьшается до -∞ (программа зацикливает). Это обнаруживается,
когда некоторые диагональные элементы становятся отрицательными.
Слайд 65ФЛОЙД, Роберт В (Robert W Floyd, 1936 – 2001) — американский учёный в области
В Стэнфорде Флойд тесно работал с Дональдом Кнутом, в том числе в качестве главного редактора серии его знаменитых книг «Искусство программирования».
