- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свойства равнобедренного треугольника презентация
Содержание
- 1. Свойства равнобедренного треугольника
- 2. Треугольник называется равнобедренным, если две его стороны
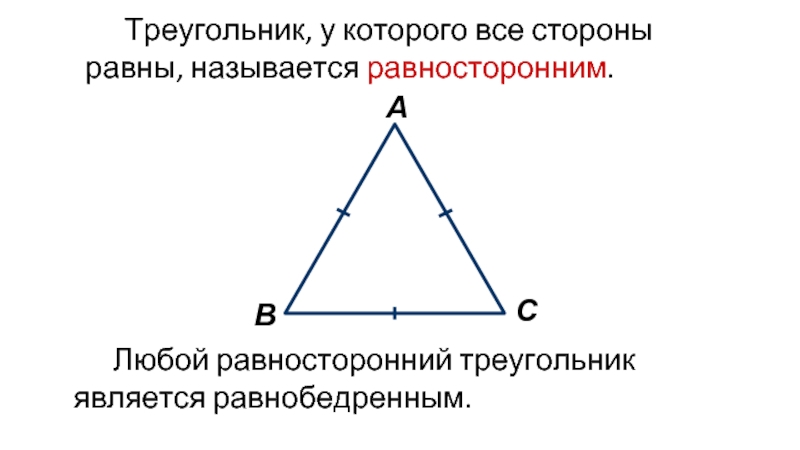
- 3. Любой равносторонний треугольник является равнобедренным.
- 4. Теорема. В равнобедренном треугольнике углы при основании
- 5. Теорема. В равнобедренном треугольнике биссектриса, проведённая к
- 6. Высота равнобедренного треугольника, проведённая к основанию, является
- 7. Задача. АВСD – квадрат. Точка Е –
- 8. Задача. В равнобедренном треугольнике АВС, где АВ
Треугольник называется равнобедренным, если две его стороны равны. АВ, АС – боковые стороны ∆ АВС.
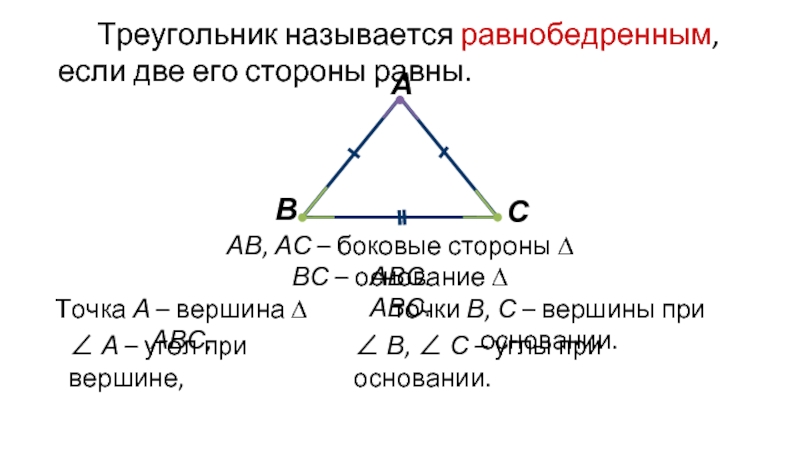
Слайд 2Треугольник называется равнобедренным, если две его стороны равны.
АВ, АС –
боковые стороны ∆ АВС.
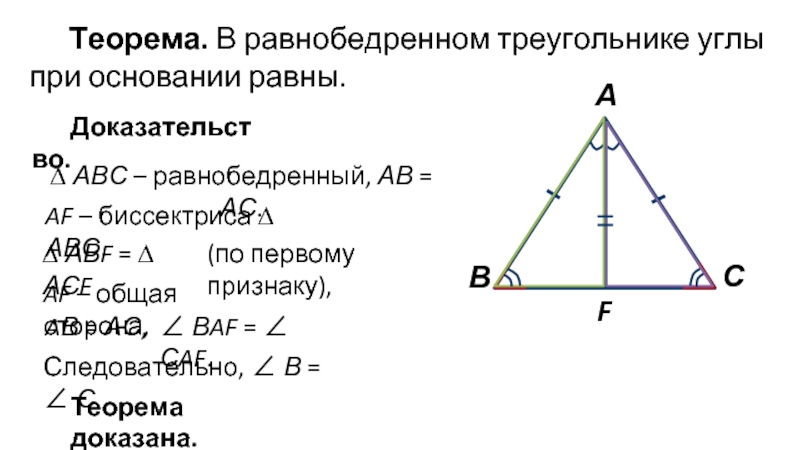
Слайд 4Теорема. В равнобедренном треугольнике углы при основании равны.
Доказательство.
AВ = АС,
∠ ВAF = ∠ СAF.
Теорема доказана.
(по первому признаку),
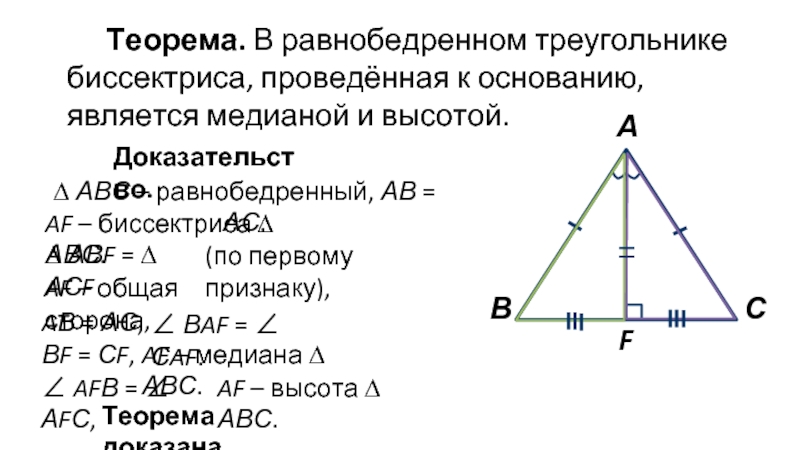
Слайд 5Теорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и
высотой.
Доказательство.
AВ = АС,
∠ ВAF = ∠ СAF.
AF – медиана ∆ АВС.
∠ AFВ = ∠ АFС,
AF – высота ∆ АВС.
Теорема доказана.
(по первому признаку),
Слайд 6Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
Медиана равнобедренного
треугольника, проведённая к основанию, является высотой и биссектрисой.
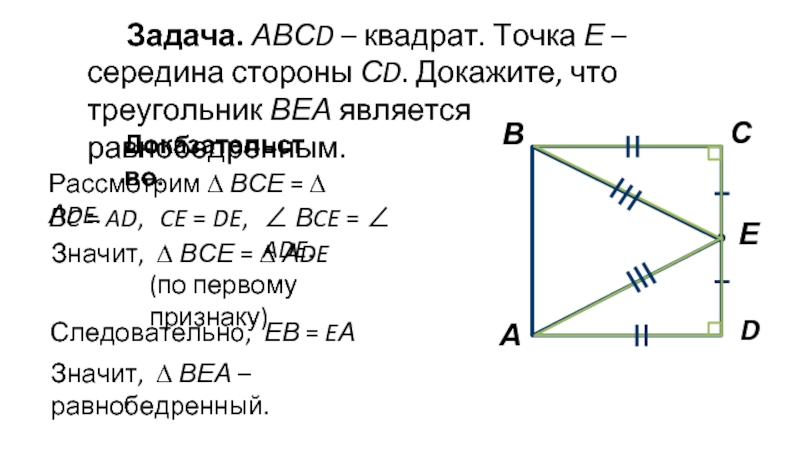
Слайд 7Задача. АВСD – квадрат. Точка Е – середина стороны СD. Докажите,
что треугольник ВЕА является равнобедренным.
Доказательство.
Рассмотрим ∆ ВСЕ = ∆ АDE.
CE = DE,
∠ ВCE = ∠ ADE.
Значит, ∆ ВСЕ = ∆ АDE
(по первому признаку).
Следовательно, ЕВ = EА
Значит, ∆ ВЕА – равнобедренный.
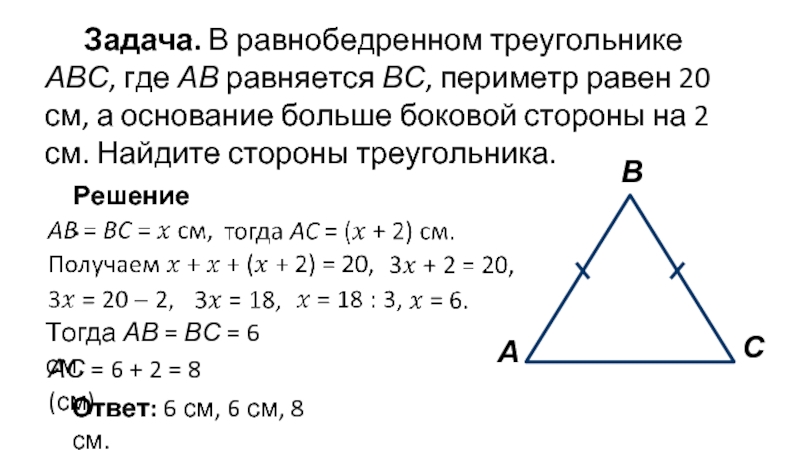
Слайд 8Задача. В равнобедренном треугольнике АВС, где АВ равняется ВС, периметр равен
20 см, а основание больше боковой стороны на 2 см. Найдите стороны треугольника.
Решение.
Тогда АВ = ВС = 6 см,
АС = 6 + 2 = 8 (см).
Ответ: 6 см, 6 см, 8 см.
