- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Степенные функции, их свойства и графики презентация
Содержание
- 1. Степенные функции, их свойства и графики
- 2. Степенными функциями называются функции вида у = хr, где r – заданное рациональное число
- 3. y x -1 0
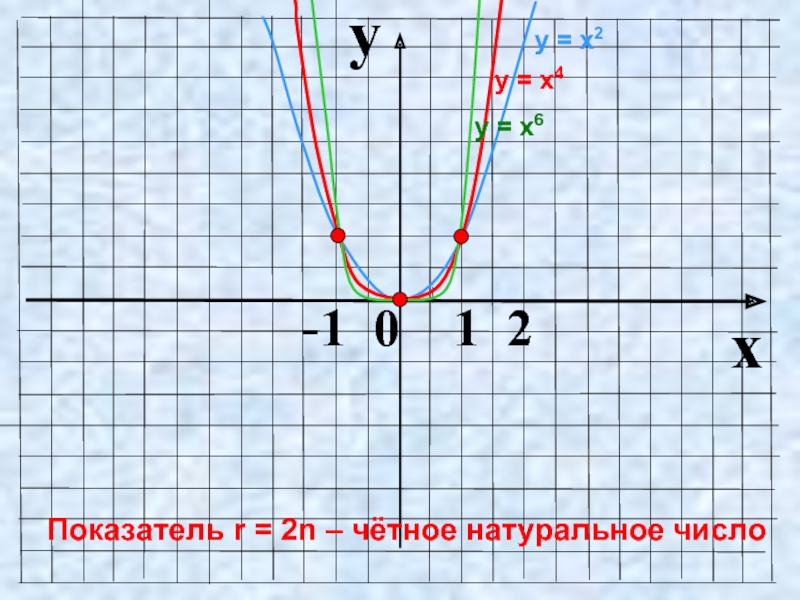
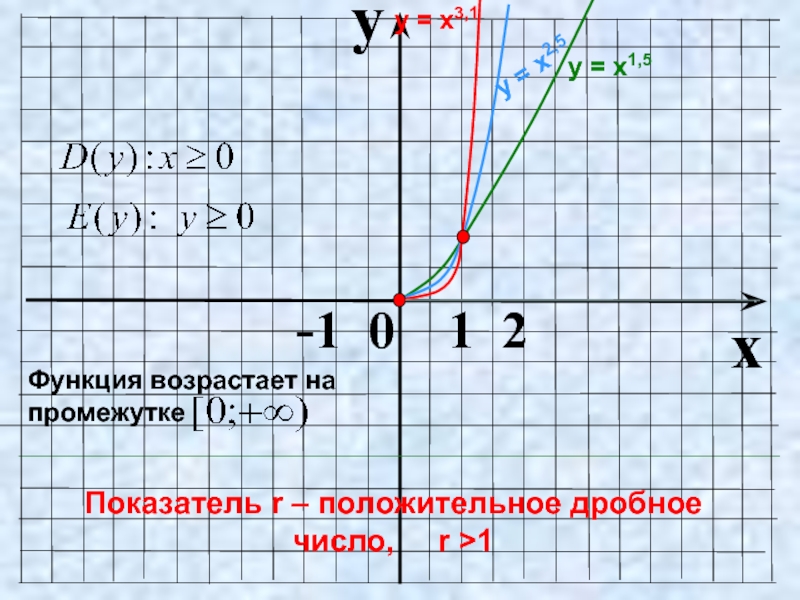
- 4. Показатель r = 2n – чётное натуральное
- 5. y x -1 0
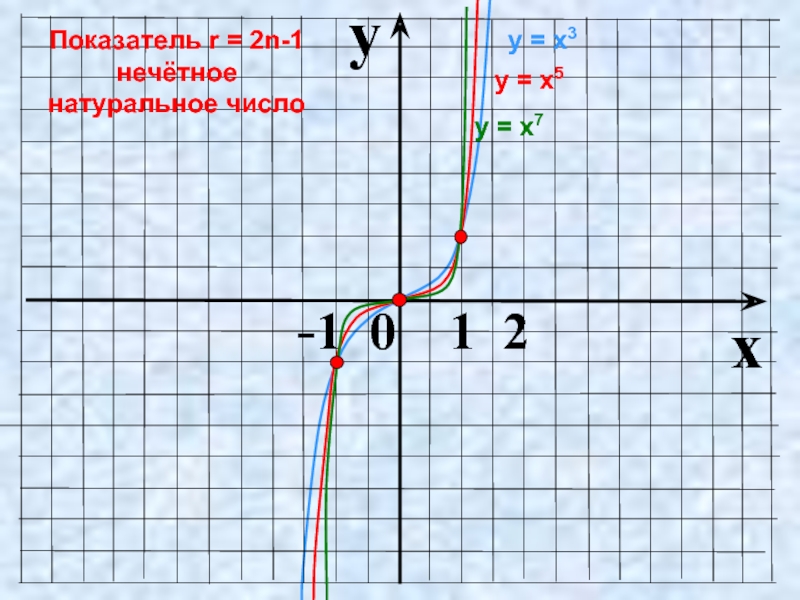
- 6. Показатель r = 2n-1 – нечётное
- 7. y x -1 0
- 8. Показатель r = – (2n-1), где n
- 9. y x -1 0
- 10. Показатель r = – 2n, где n
- 11. y x -1 0
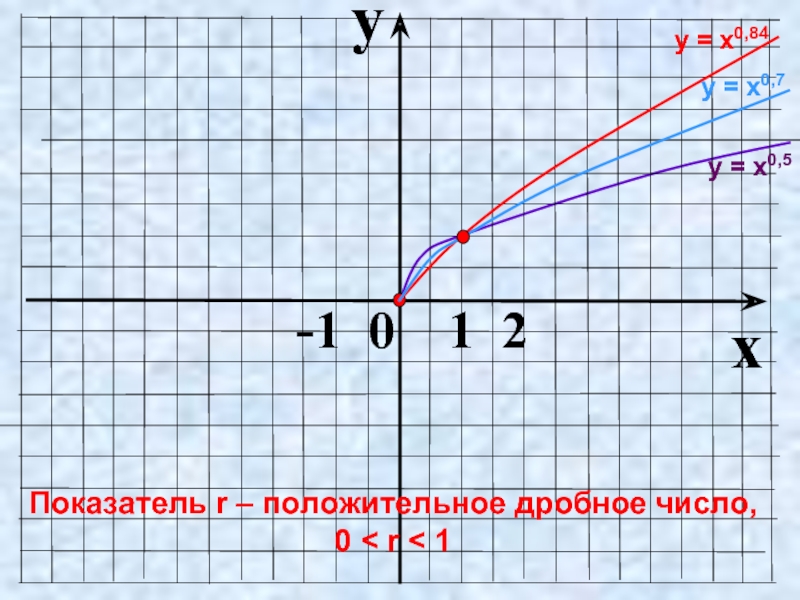
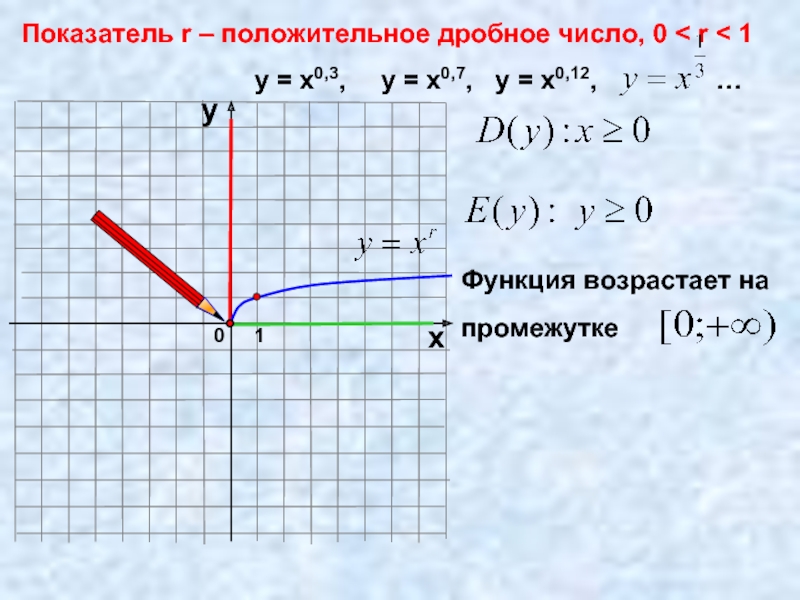
- 12. 0 Показатель r – положительное дробное число,
- 13. y x -1 0
- 14. y x -1 0
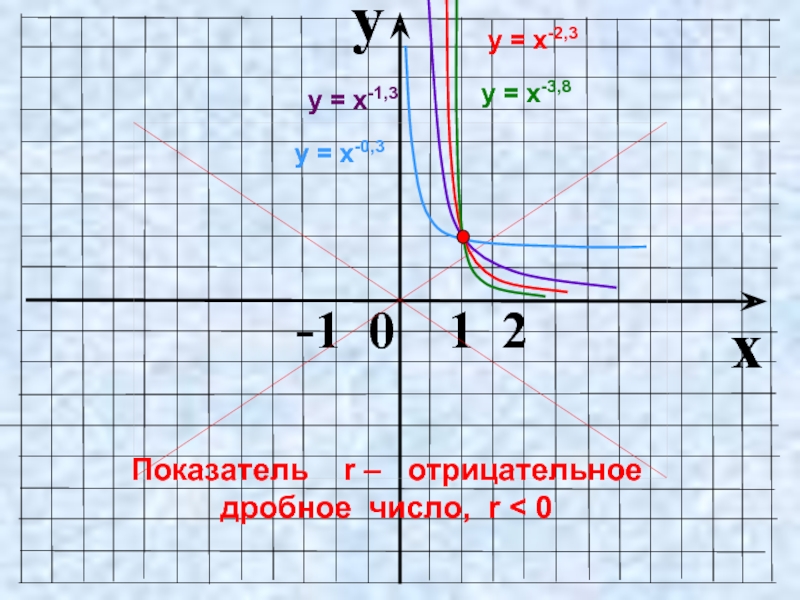
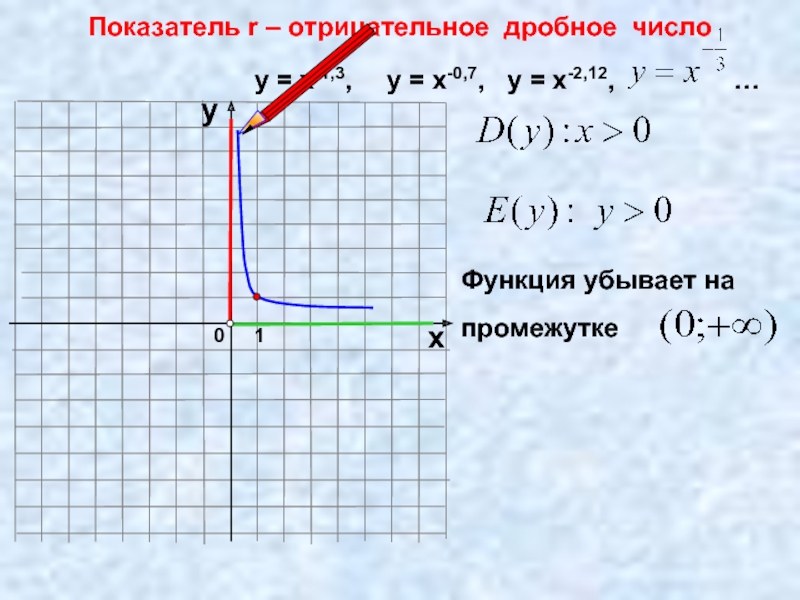
- 15. 0 Показатель r – отрицательное дробное число
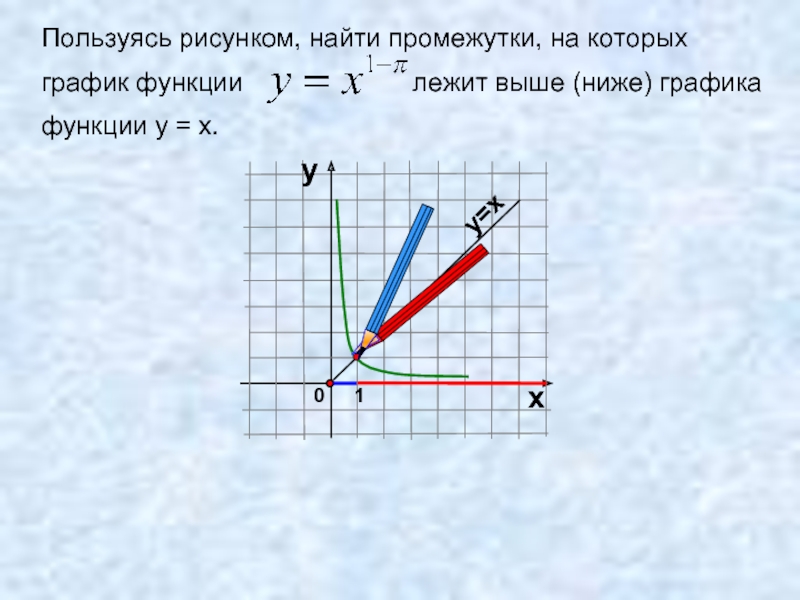
- 17. Пользуясь рисунком, найти промежутки, на которых
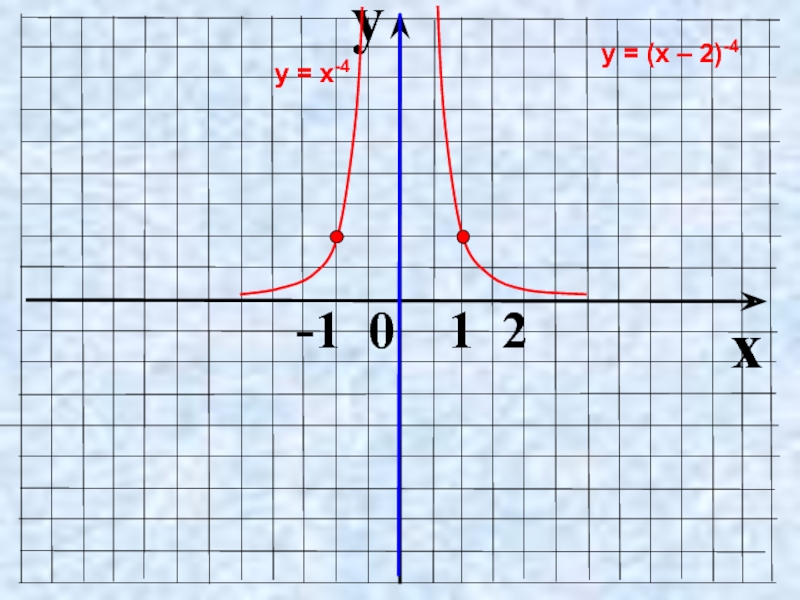
- 18. Пользуясь рисунком, найти промежутки, на которых
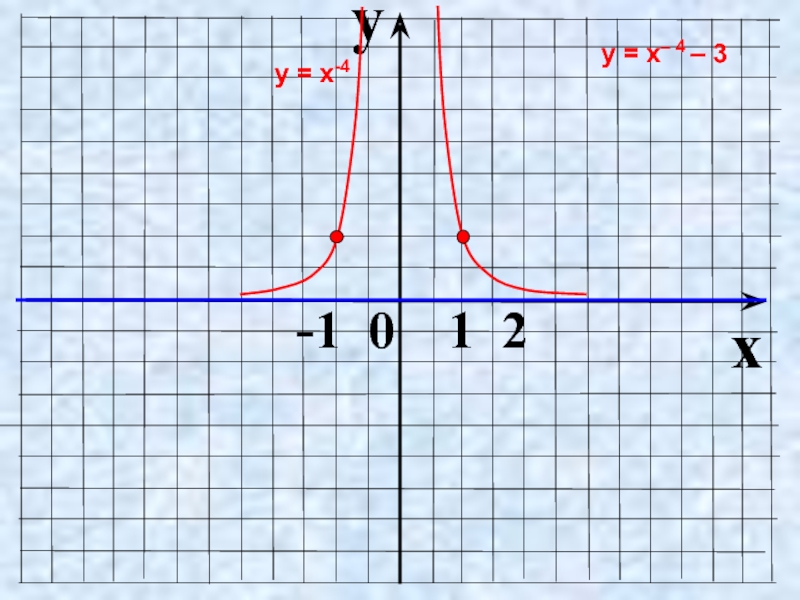
- 19. Пользуясь рисунком, найти промежутки, на которых
- 20. Преобразования графиков степенных функций
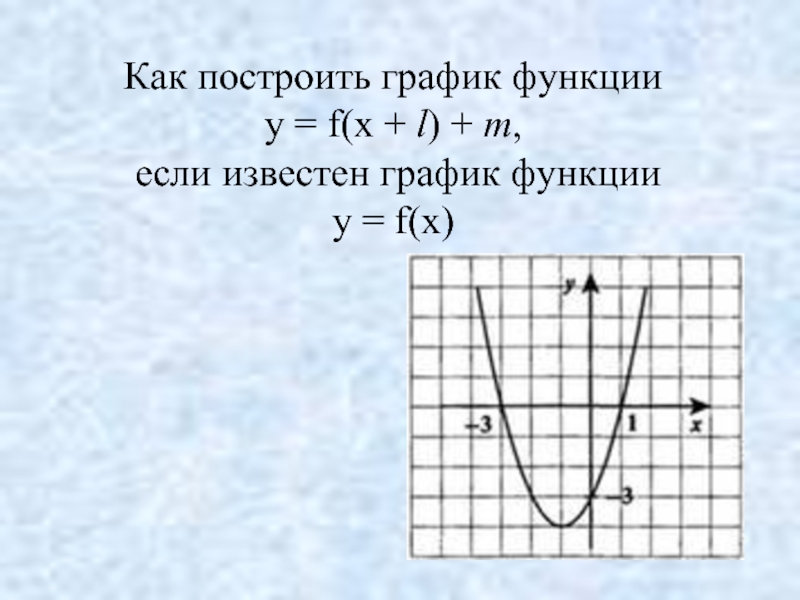
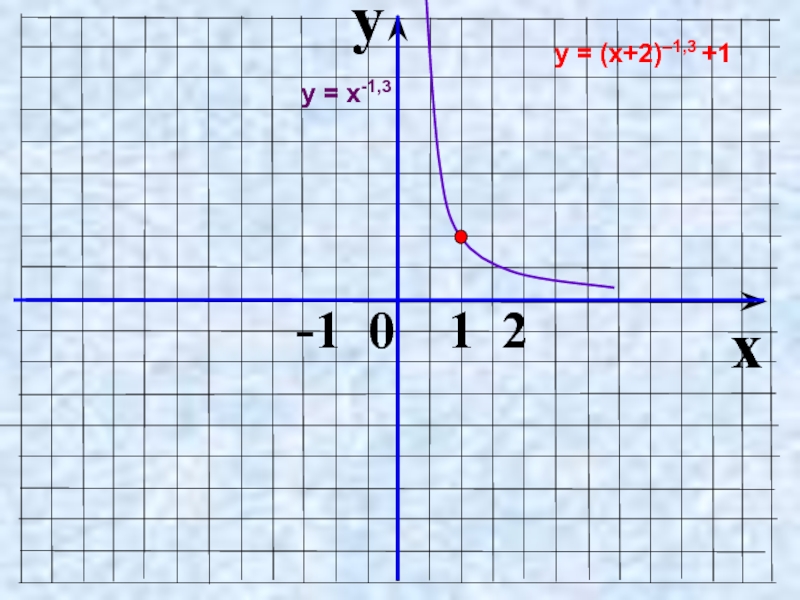
- 21. Как построить график функции y =
- 22. y x -1 0
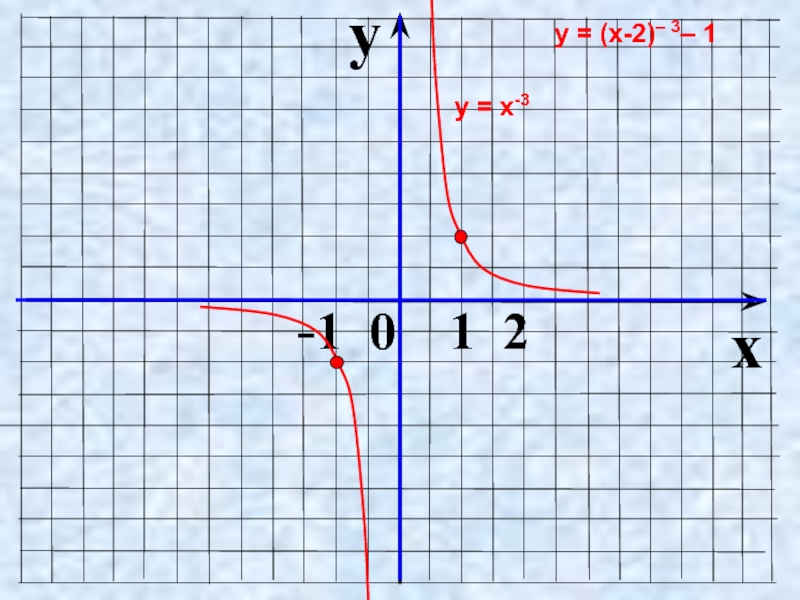
- 23. Как построить график функции y =
- 24. y x -1 0
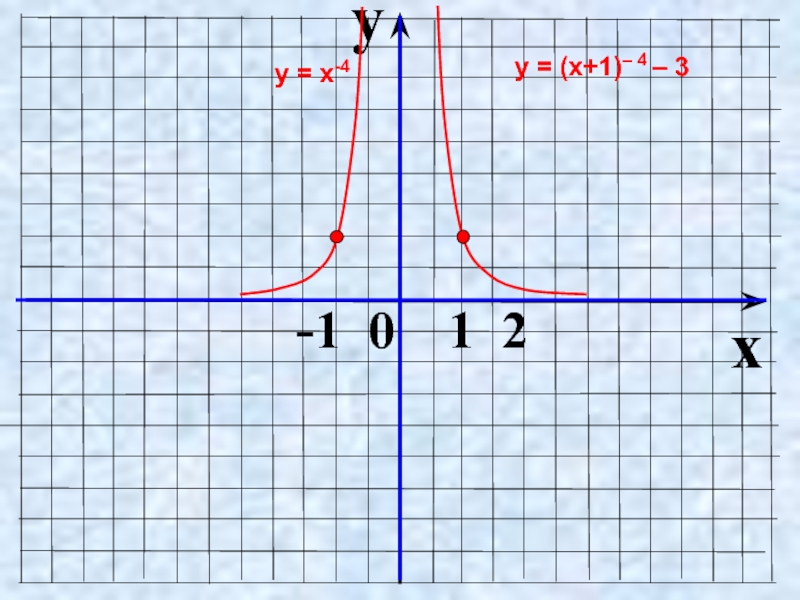
- 25. Как построить график функции y =
- 26. y x -1 0
- 27. y x -1 0
- 28. y x -1 0
- 29. Пример 1. Найдём производную функции: При этом было использовано правило дифференцирования
- 30. Пример 2. Исследуем функцию На монотонность и
- 31. Пример 2. Исследуем функцию На монотонность и
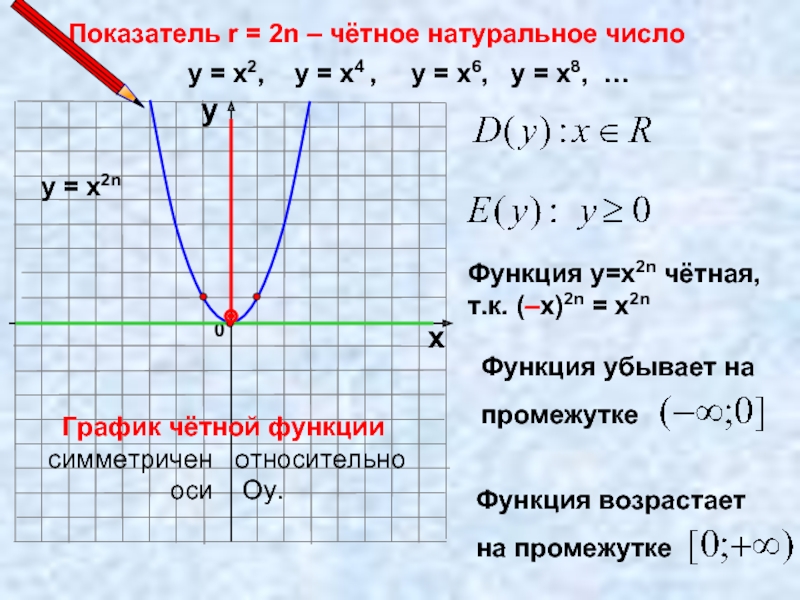
Слайд 4Показатель r = 2n – чётное натуральное число
0
х
у
у = х2,
у = х2n
Функция у=х2n чётная,
т.к. (–х)2n = х2n
График чётной функции
симметричен относительно
оси Оу.
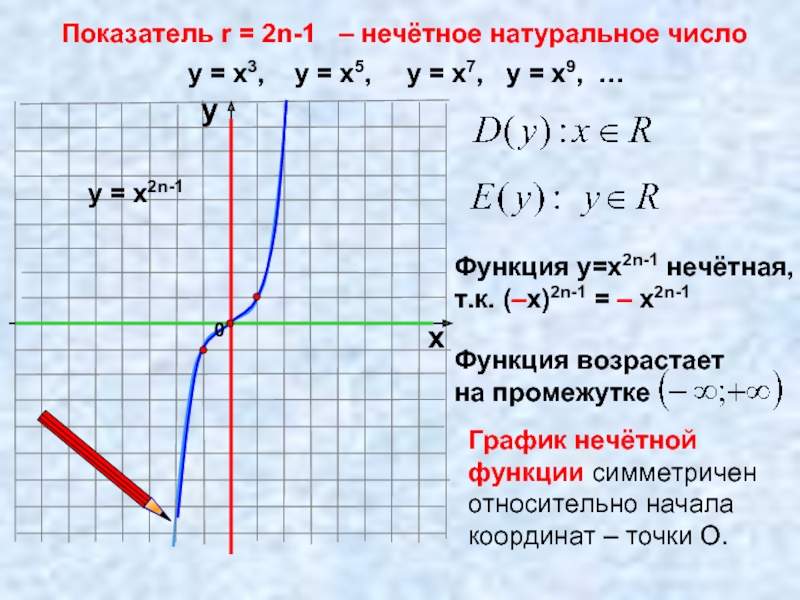
Слайд 6Показатель r = 2n-1 – нечётное натуральное число
х
у
у = х3,
у = х2n-1
Функция у=х2n-1 нечётная,
т.к. (–х)2n-1 = – х2n-1
0
График нечётной функции симметричен относительно начала координат – точки О.
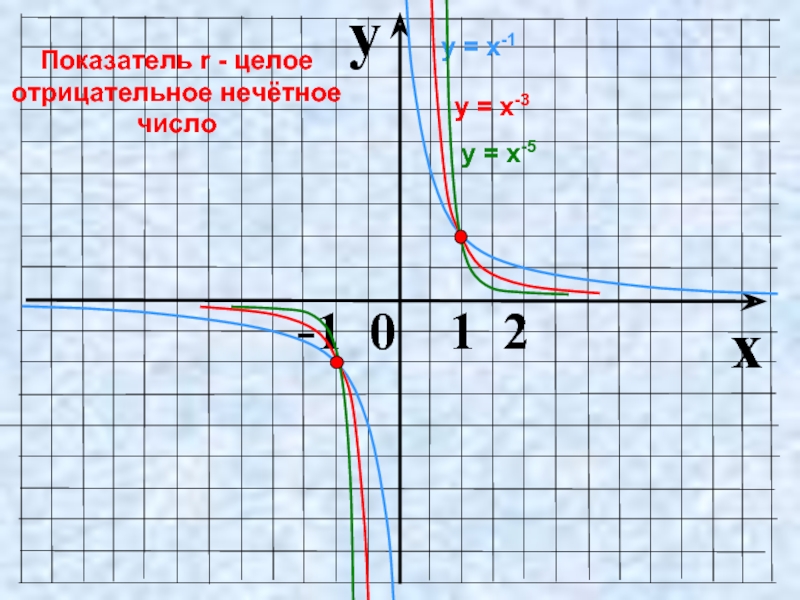
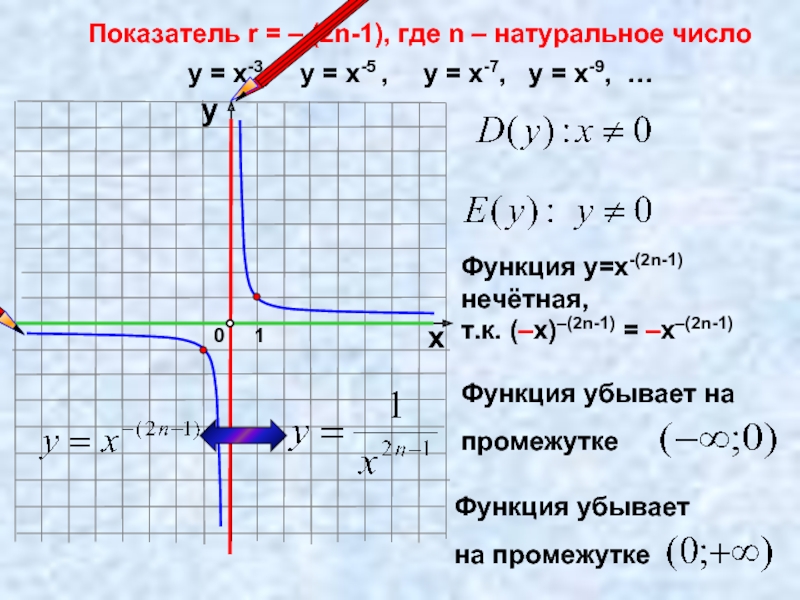
Слайд 8Показатель r = – (2n-1), где n – натуральное число
1
0
х
у
у =
Функция у=х-(2n-1) нечётная,
т.к. (–х)–(2n-1) = –х–(2n-1)
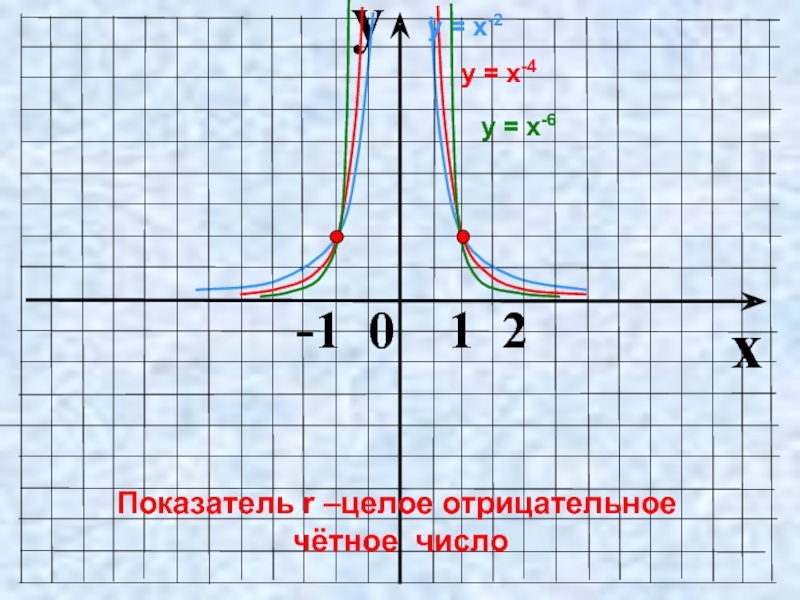
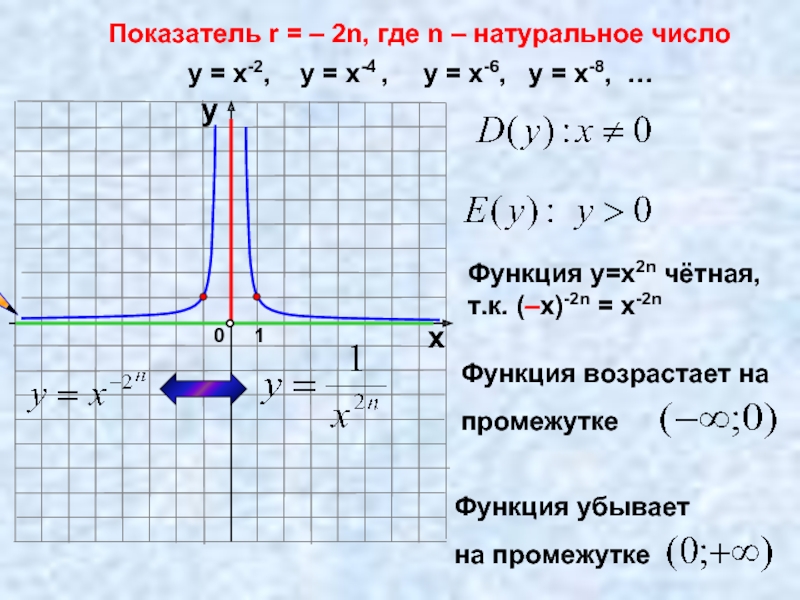
Слайд 10Показатель r = – 2n, где n – натуральное число
1
0
х
у
у =
Функция у=х2n чётная,
т.к. (–х)-2n = х-2n
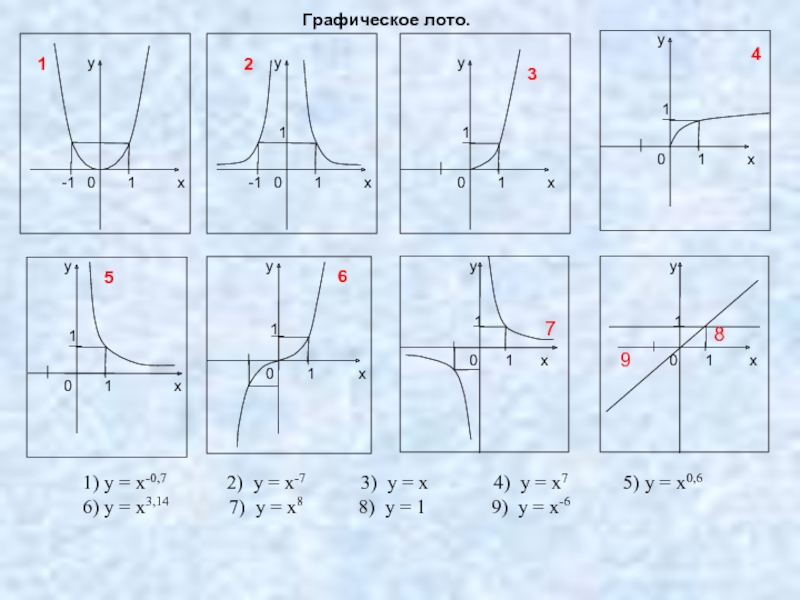
Слайд 16
8
7
9
1) у = х-0,7 2) у = х-7 3) у = х 4) у = х7 5) у = х0,6
6) у = х3,14 7) у = х8 8) у = 1 9) у = х-6
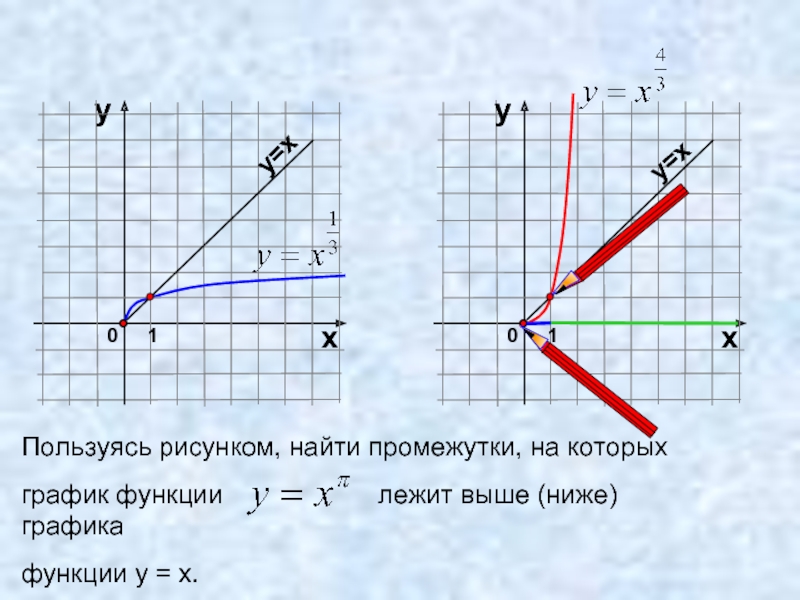
Слайд 17Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.
0
1
х
у
у=х
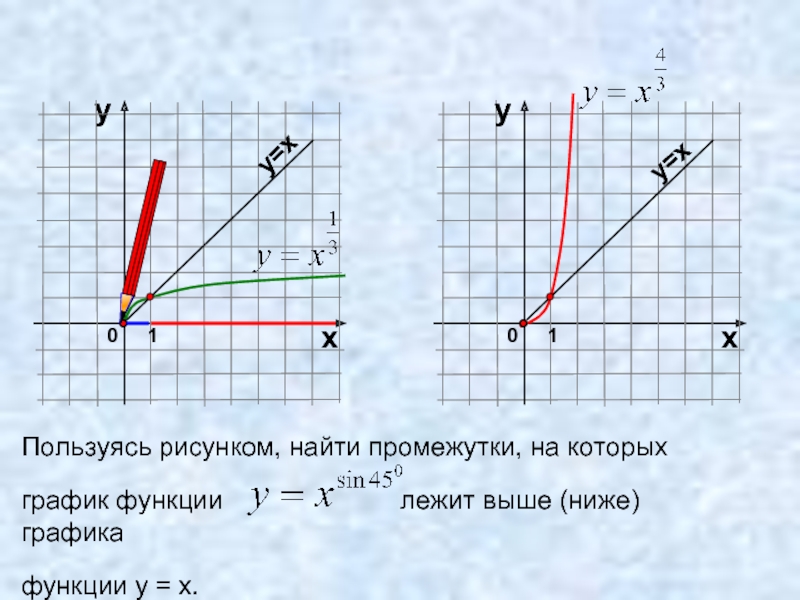
Слайд 18Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.
у
0
1
х
у=х
Слайд 19Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.
Слайд 30Пример 2.
Исследуем функцию
На монотонность и экстремумы и
построим её график.
1. Найдём
2. Функция существует при х ≥ 0, производная существует при х>0. Поэтому критических точек у функции нет. Стационарную точку найдём из условия или , откуда х=1.
3. Очевидно, что при х (0;1], значение у'≤0 и функция у(х) убывает на этом промежутке. При х [1;+∞) значение у'≥0 и функция у(х) возрастает. В точке х = 1 функция у(х) имеет минимум
э
э
Слайд 31Пример 2.
Исследуем функцию
На монотонность и экстремумы и
построим её график.
1. Найдём
2. Функция существует при х ≥ 0, производная существует при х>0. Поэтому критических точек у функции нет. Стационарную точку найдём из условия или , откуда х=1.
3. Очевидно, что при х (0;1], значение у'≤0 и функция у(х) убывает на этом промежутке. При х [1;+∞) значение у'≥0 и функция у(х) возрастает. В точке х = 1 функция у(х) имеет минимум
э
э