- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стаціонарні випадкові процеси презентация
Содержание
- 1. Стаціонарні випадкові процеси
- 2. Стаціонарні випадкові процеси
- 3. Стаціонарні випадкові процеси
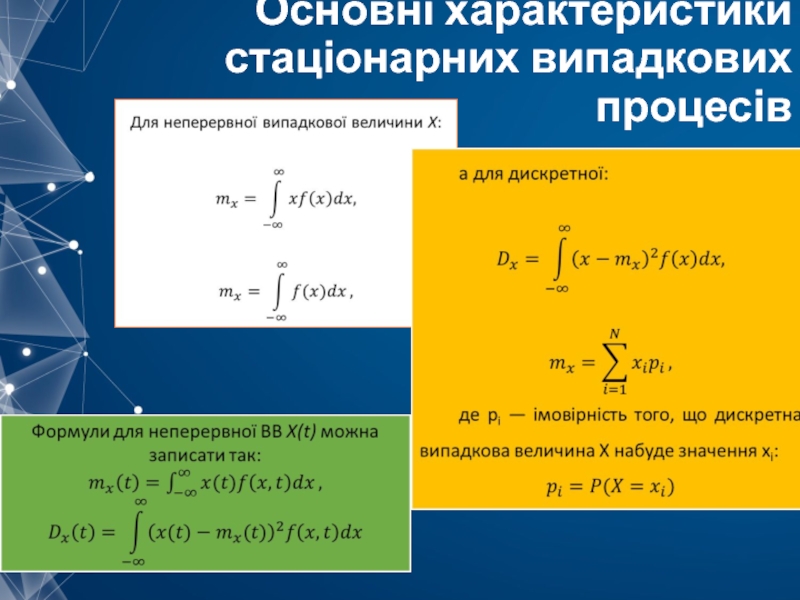
- 4. Основні характеристики стаціонарних випадкових процесів Означення. Строга
- 5. Основні характеристики стаціонарних випадкових процесів Всі ці
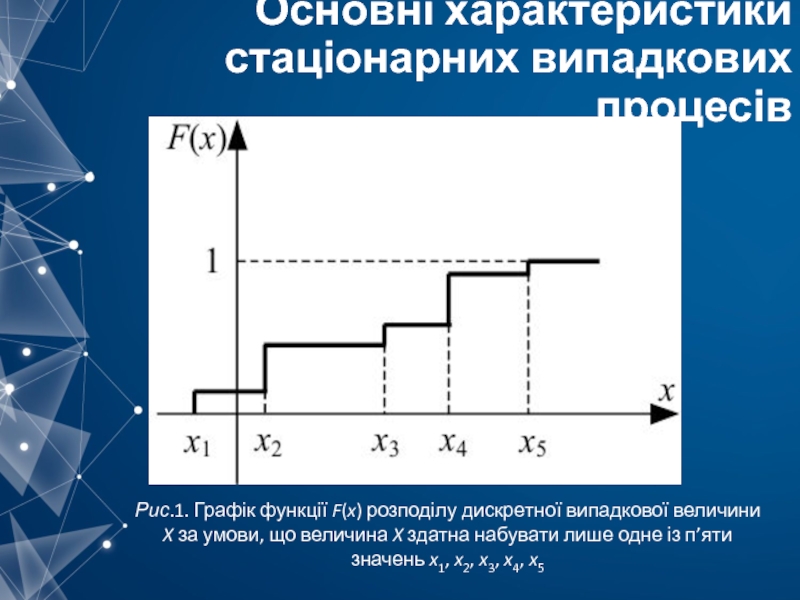
- 6. Основні характеристики стаціонарних випадкових процесів Рис.1. Графік
- 7. Основні характеристики стаціонарних випадкових процесів
- 8. Основні характеристики стаціонарних випадкових процесів У
- 9. Основні характеристики стаціонарних випадкових процесів Але у
- 10. Основні характеристики стаціонарних випадкових процесів
- 11. Стаціонарно зв'язані випадкові функції Означення. Стаціонарно зв'язаними
- 12. Диференціювання стаціонарного випадкового процесу Теорема. Перша
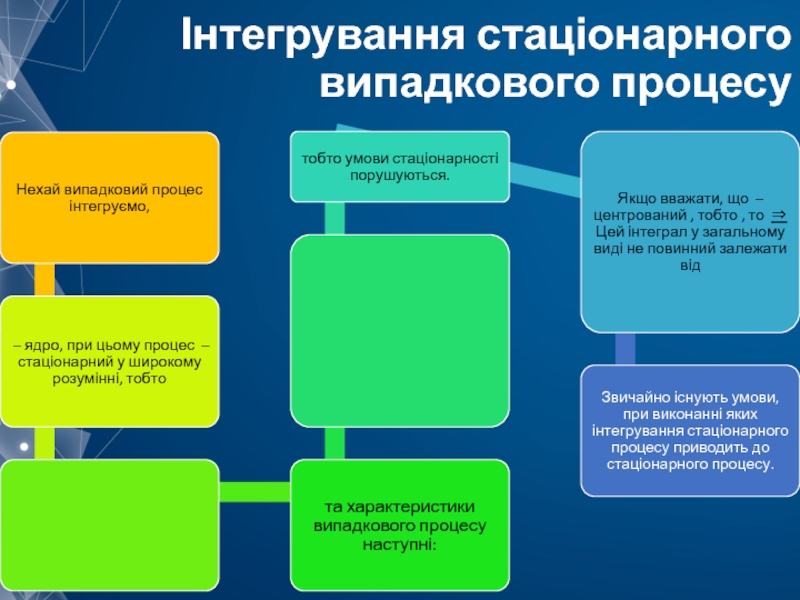
- 13. Інтегрування стаціонарного випадкового процесу
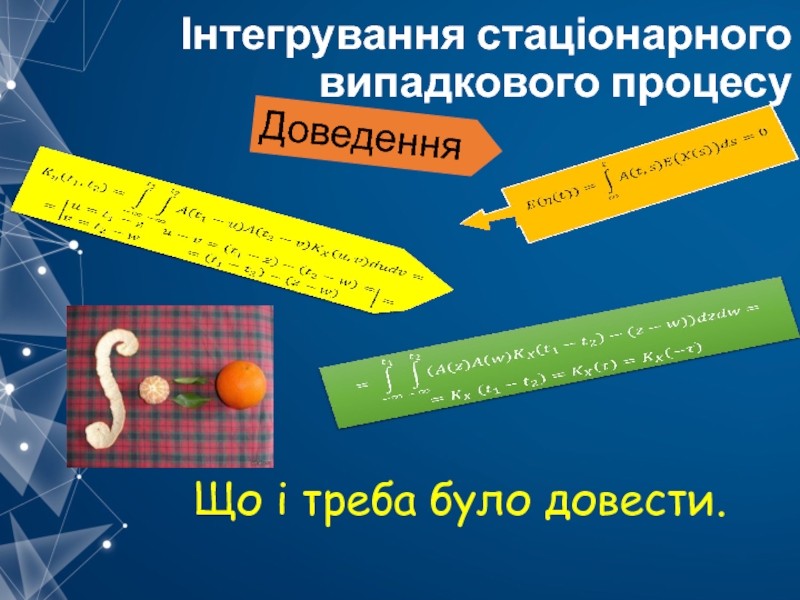
- 14. Інтегрування стаціонарного випадкового процесу Доведення Що і треба було довести.
- 15. Кореляційні функції та спектральні густини стаціонарних випадкових
- 16. Кореляційні функції та спектральні густини стаціонарних випадкових
- 17. Кореляційні функції та спектральні густини стаціонарних випадкових
- 18. Кореляційні функції та спектральні густини стаціонарних випадкових
- 19. Кореляційні функції та спектральні густини стаціонарних випадкових
- 20. Кореляційні функції та спектральні густини стаціонарних випадкових процесів
- 21. Кореляційні функції та спектральні густини стаціонарних випадкових
- 22. Кореляційні функції та спектральні густини стаціонарних випадкових
- 23. Кореляційні функції та спектральні густини стаціонарних випадкових
- 24. Кореляційні функції та спектральні густини стаціонарних випадкових
- 25. Кореляційні функції та спектральні густини стаціонарних випадкових
- 26. Кореляційні функції та спектральні густини стаціонарних випадкових процесів
- 27. Кореляційні функції та спектральні густини стаціонарних випадкових
- 28. Кореляційні функції та спектральні густини стаціонарних випадкових
- 29. Кореляційні функції та спектральні густини стаціонарних випадкових
- 30. Кореляційні функції та спектральні густини стаціонарних випадкових процесів
- 31. Властивості кореляційної функції стаціонарної функції
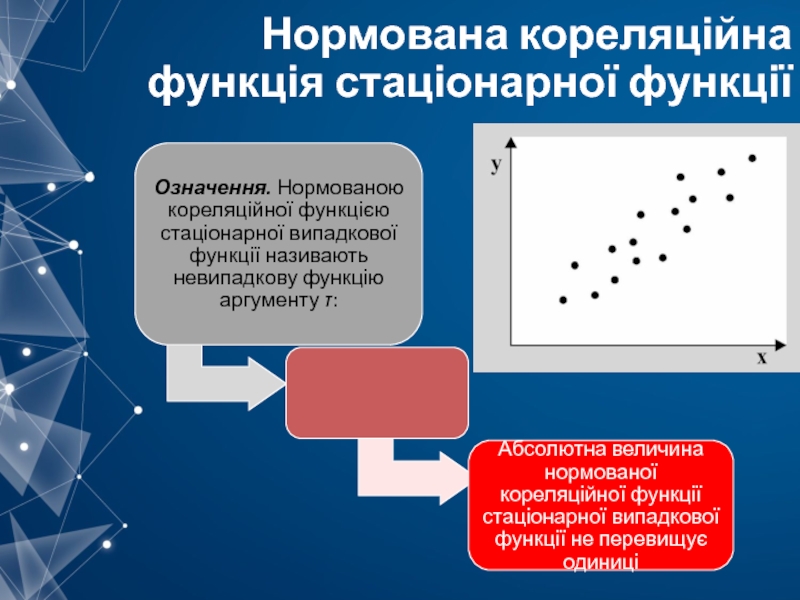
- 32. Нормована кореляційна функція стаціонарної функції
- 33. Кореляційна функція похідної та інтеграла стаціонарної функції
- 34. Кореляційна функція похідної та інтеграла стаціонарної функції
Слайд 4Основні характеристики стаціонарних випадкових процесів
Означення. Строга математична модель безперервного випадкового процесу
Перша із цих властивостей означає, що графік функції розподілу безперервної випадкової величини X є безперервною зростаючою зі зростанням аргументу x кривою.
Друга властивість означає, що випадкова величина X не може мати значень, менших від мінус нескінченності.
Слайд 5Основні характеристики стаціонарних випадкових процесів
Всі ці властивості є справедливими і для
Третя властивість означає, що випадкова величина X не може мати значень, більших від плюс нескінченності.
А четверта властивість означає, що для знаходження ймовірності потрапляння випадкової величини X у проміжок значень [x1, x2) достатньо взяти різницю значень її функції розподілу F(x) на границях цього проміжку.
Слайд 6Основні характеристики стаціонарних випадкових процесів
Рис.1. Графік функції F(x) розподілу дискретної випадкової
Слайд 8Основні характеристики стаціонарних випадкових процесів
У класі стаціонарних випадкових процесів X(t) виділяють
Слайд 9Основні характеристики стаціонарних випадкових процесів
Але у практиці розрахунків використовуються дещо інші
за якими знаходяться статистична оцінка mx* математичного очікування mx ергодичного випадкового процесу X(t) та статистична оцінка Dx* дисперсії Dx цього процесу з використанням однієї, але достатньо інформативної реалізації x*(t) випадкового процесу X(t), зафіксованої на відрізку часу T.
Оцінки mx* та Dx* теж є випадковими величинами, залежними від довжини T реалізації x*(t), але, зрозуміло, що дисперсія цих оцінок є набагато меншою у порівнянні із дисперсією процесу X(t) і з ростом T наближається до нуля.
Слайд 11Стаціонарно зв'язані випадкові функції
Означення. Стаціонарно зв'язаними називають дві випадкові функції X(t)
Rxy(t1,t2) = rxy(τ).
Взаємна кореляційна функція стаціонарно зв'язаних випадкових функцій має наступну властивість:
rxy(τ) = ryx (-τ).
Слайд 12Диференціювання стаціонарного випадкового процесу
Теорема. Перша похідна від стаціонарного процесу, є стаціонарним
Всі умови Хінчина виконуються. Тобто диференціювання стаціонарного процесу приводить до стаціонарного процесу.
Слайд 15Кореляційні функції та спектральні густини стаціонарних випадкових процесів
Для оцінювання лінійного зв’язку
де f(x1,x2,t1,t2) — двовимірна густина ймовірностей випадкового процесу X(t), котра визначається у моменти часу t1,t2, відносно яких випадковий процес X(t) можна розглядати як систему двох випадкових величин X1 та X2, значеннями x1 та x2 яких є значення x(t1), x(t2) реалізацій випадкового процесу, зафіксовані у моменти часу t1, t2:
Слайд 16Кореляційні функції та спектральні густини стаціонарних випадкових процесів
F(x1,x2,t1,t2) — двовимірна функція
Формула (*) грає не стільки практичну, скільки загальнотеоретичну роль, оскільки на практиці ніхто не проводить оцінювання функцій f(x1,x2,t1,t2) та F(x1,x2,t1,t2) за експериментальними даними.
Слайд 17Кореляційні функції та спектральні густини стаціонарних випадкових процесів
Формула (*) навіть у
З урахуванням (**), формула для кореляційної функції стаціонарного випадкового процесу X(t) набуває вигляду:
Слайд 18Кореляційні функції та спектральні густини стаціонарних випадкових процесів
Але і формулу (•)
Очевидно, що чим більшим є значення T, тим точніше оцінка Kx*(τ) відображає кореляційну функцію Kx(τ).
Слайд 19Кореляційні функції та спектральні густини стаціонарних випадкових процесів
який констатує той факт,
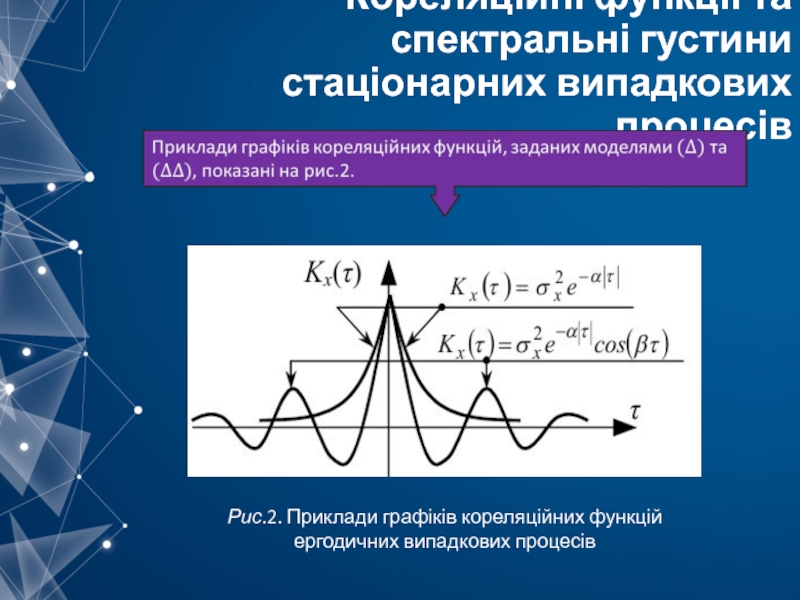
Слайд 21Кореляційні функції та спектральні густини стаціонарних випадкових процесів
Рис.2. Приклади графіків кореляційних
Слайд 22Кореляційні функції та спектральні густини стаціонарних випадкових процесів
Для характеристики усередненого лінійного
відповідно, двовимірні взаємні густина f та функція розподілу F ймовірностей процесів X(t) та Y(t).
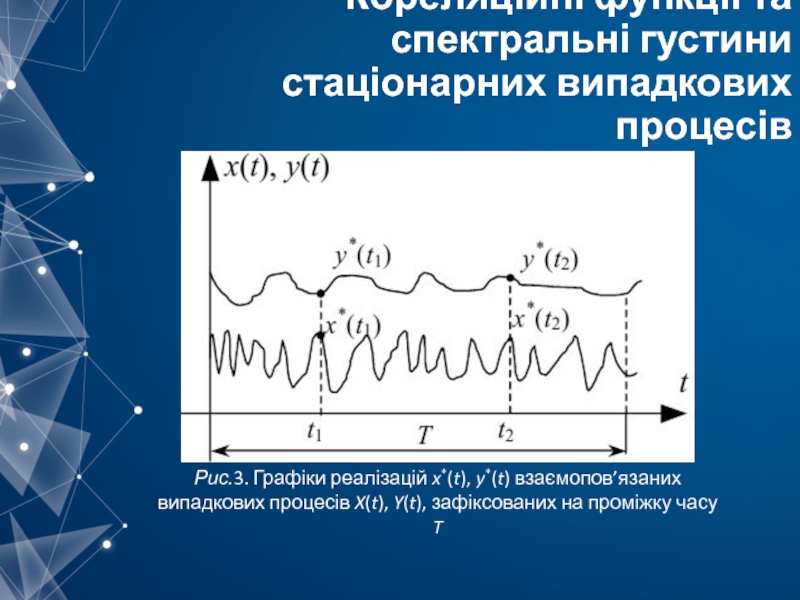
Слайд 23Кореляційні функції та спектральні густини стаціонарних випадкових процесів
Рис.3. Графіки реалізацій x*(t),
Слайд 24Кореляційні функції та спектральні густини стаціонарних випадкових процесів
Для стаціонарних випадкових процесів
а для ергодичних випадкових процесів за аналогією з (••), (◊◊):
Слайд 25Кореляційні функції та спектральні густини стаціонарних випадкових процесів
тоді отримаємо іншу характеристику
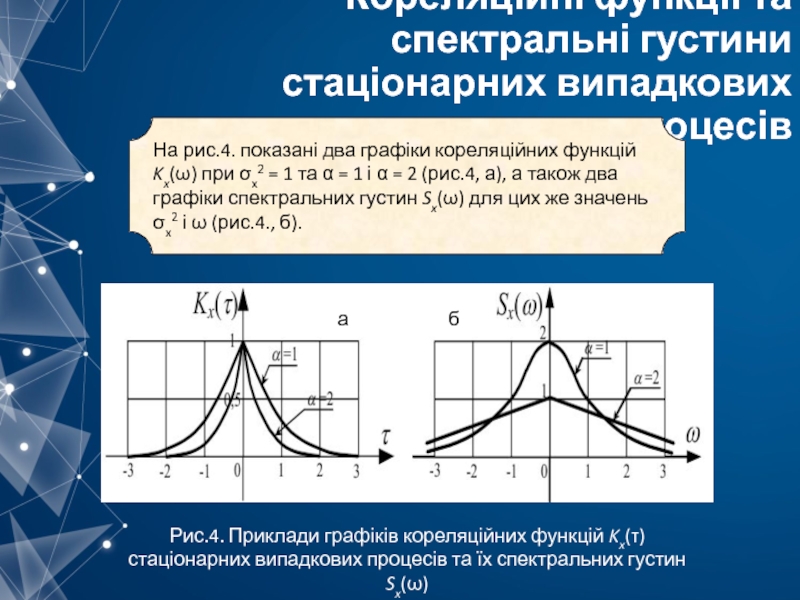
Слайд 27Кореляційні функції та спектральні густини стаціонарних випадкових процесів
На рис.4. показані два
Рис.4. Приклади графіків кореляційних функцій Kx(τ) стаціонарних випадкових процесів та їх спектральних густин Sx(ω)
а б
Слайд 28Кореляційні функції та спектральні густини стаціонарних випадкових процесів
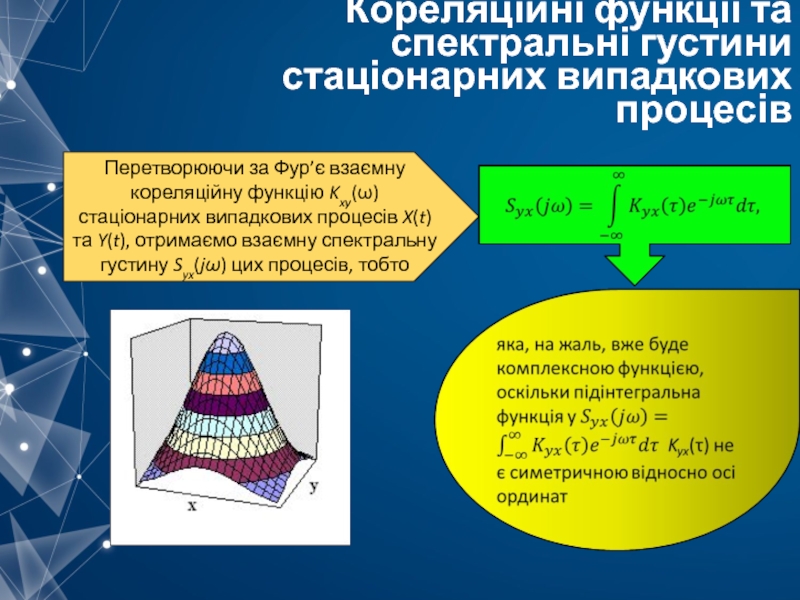
Перетворюючи за Фур’є взаємну
Слайд 29Кореляційні функції та спектральні густини стаціонарних випадкових процесів
Особливу роль під час
Якщо підставити (58) у (55), то отримаємо: