- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистическое оценивание. Выборочный метод. Требования, предъявляемые к выборке. (Лекция 4) презентация
Содержание
- 1. Статистическое оценивание. Выборочный метод. Требования, предъявляемые к выборке. (Лекция 4)
- 2. План лекции: Выборочный метод. Требования, предъявляемые к
- 3. Выборочный метод. Требования, предъявляемые
- 4. Совокупность из которой отбирается некоторая часть ее
- 5. Часть генеральной совокупности отобранная тем или иным
- 6. Выборочный метод является основным при изучении статистических
- 7. Выборка должна быть представительной – репрезентативной
- 8. Рендомизация (от англ. random - случай) –
- 9. Способы отбора вариант из генеральной совокупности: Повторный
- 10. Виды отбора единиц из генеральной совокупности: Типический (или групповой); Серийный (или гнездовой); Механический.
- 11. Механический отбор (систематический) - когда образцы
- 12. Таблица случайных чисел
- 13. Послойная выборка Рандомизацию проводят дифференцированно для каждой
- 14. Процесс систематизации или упорядочения, первичных биометрических данных
- 15. Статистические оценки генеральных параметров.
- 16. Так как характеристикой варьирования оценок около своего
- 17. Равенство или неравенство математических ожиданий оценок и
- 18. Требования, предъявляемые к оценкам Состоятельность Точечные
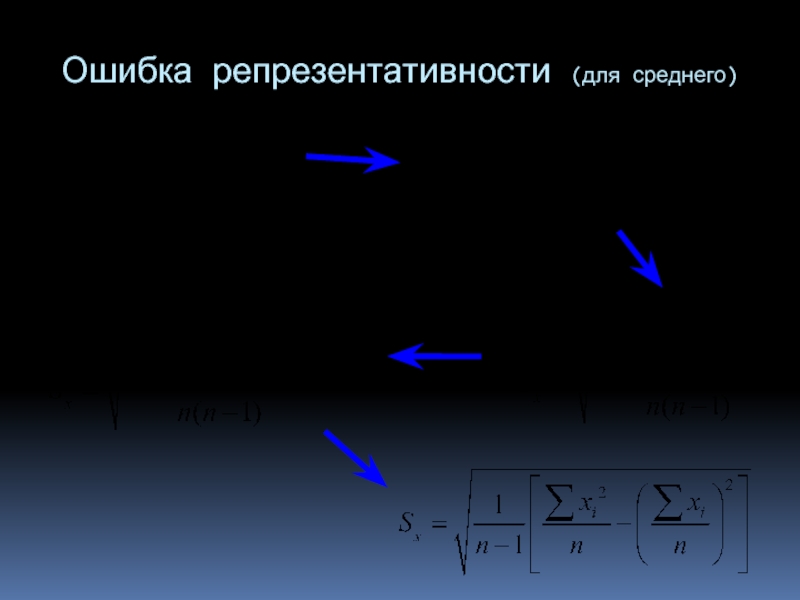
- 19. Ошибка репрезентативности (для среднего)
- 20. Если средняя арифметическая вычисляется способом условной средней ее ошибка определяется как:
- 21. ФОРМУЛА ОШИБКИ ВЫБОРОЧНОЙ СРЕДНЕЙ ПРИ БЕСПОВТОРНОЙ ВЫБОРКЕ
- 22. Показатель точности определения средней
- 23. Ошибка выборочной доли
- 24. Определение объема выборки
- 25. Оценка дисперсии Оценка среднего квадратического отклонения
- 26. Оценка коэффициента вариации или
- 27. Оценка медианы
- 28. Интервальные оценки
- 29. Вероятности, признанные достаточными, для суждений о генеральных
- 30. Здесь при Р=0,95 есть риск ошибиться
- 31. Нормированное отклонение – показатель представляющий отклонение той
- 32. Вероятность отклонения любой варианты (хi) нормально
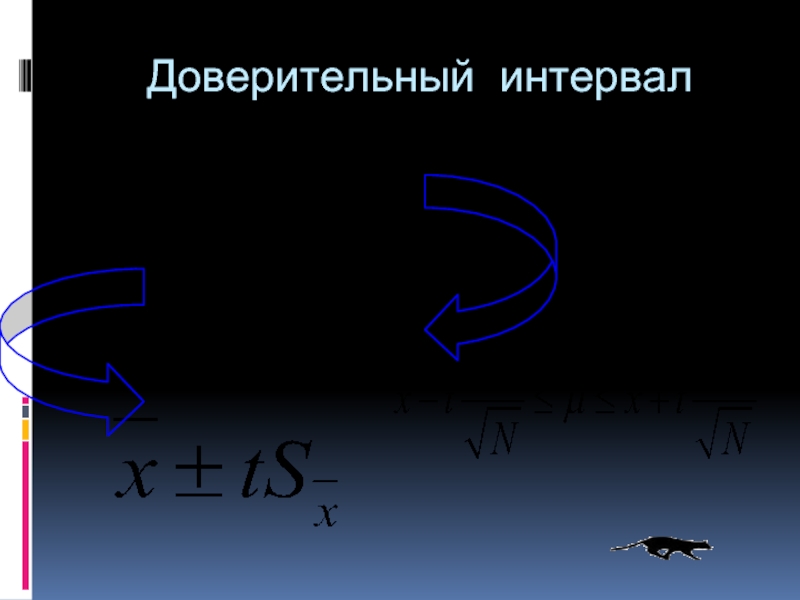
- 33. Доверительный интервал
- 35. Спасибо за внимание!
План лекции: Выборочный метод. Требования, предъявляемые к выборке. Рандомизация. Способы отбора вариант в выборку. Понятие статистической оценки. Точечные и интервальные оценки. Несмещенность, состоятельность и эффективность оценок.
Слайд 2План лекции:
Выборочный метод. Требования, предъявляемые к выборке. Рандомизация. Способы отбора вариант
в выборку.
Понятие статистической оценки. Точечные и интервальные оценки. Несмещенность, состоятельность и эффективность оценок.
Понятие доверительного интервала. Оценки и их доверительные интервалы для математического ожидания и дисперсии нормального распределения.
Доверительные вероятности. Примеры получения оценок для почвенных данных.
Понятие статистической оценки. Точечные и интервальные оценки. Несмещенность, состоятельность и эффективность оценок.
Понятие доверительного интервала. Оценки и их доверительные интервалы для математического ожидания и дисперсии нормального распределения.
Доверительные вероятности. Примеры получения оценок для почвенных данных.
Слайд 3
Выборочный метод. Требования, предъявляемые к выборке. Рандомизация. Способы отбора вариант в
выборку.
Слайд 4Совокупность из которой отбирается некоторая часть ее членов для совместного изучения
называется генеральной.
N – объем генеральной совокупности:
N →∞
N – объем генеральной совокупности:
N →∞
Слайд 5Часть генеральной совокупности отобранная тем или иным способом называется выборочной совокупностью
(или выборкой).
n – объем выборки:
n≥2
n – объем выборки:
n≥2
Слайд 6Выборочный метод является основным при изучении статистических совокупностей.
Преимущества:
- сокращает время и
затраты труда,
- позволяет получать информацию о таких совокупностях сплошное обследование которых практически невозможно или не целесообразно.
- позволяет получать информацию о таких совокупностях сплошное обследование которых практически невозможно или не целесообразно.
Слайд 7
Выборка должна быть представительной – репрезентативной (от лат. represento –представляю), т.е.
возможно полнее отображать структуру генеральной совокупности.
Слайд 8Рендомизация (от англ. random - случай) – случайный отбор вариант из
генеральной совокупности, что обеспечивает равную возможность для всех членов генеральной совокупности попасть в состав выборки.
Слайд 9Способы отбора вариант из генеральной совокупности:
Повторный
возвращение учтенных единиц в генеральную совокупность
Бесповторный
учтенные
единицы в генеральную совокупность не возвращаются
Слайд 10Виды отбора единиц из генеральной совокупности:
Типический (или групповой);
Серийный (или гнездовой);
Механический.
Слайд 11
Механический отбор (систематический) - когда образцы для анализа отбирают через равные
интервалы расстояния (времени).
Слайд 13Послойная выборка
Рандомизацию проводят дифференцированно для каждой части (зоны, слоя и т.п.)
причем объемы подвыборок в этих частях пропорциональны доле их участия в составе целого объекта.
Слайд 14Процесс систематизации или упорядочения, первичных биометрических данных в целях извлечения заключенной
в них информации, обнаружения закономерности, которой следует изучаемое явление или процесс называется группировкой. Она может быть простой и сложной.
Группировка по одному признаку называется простой (простая таблица), по нескольким признакам - сложной (корреляционная таблица).
Группировка по одному признаку называется простой (простая таблица), по нескольким признакам - сложной (корреляционная таблица).
Слайд 16Так как характеристикой варьирования оценок около своего среднего может быть стандартное
отклонение, то применительно к оценкам его называют ошибкой оценки.
Учитывая, что размер этой ошибки является функцией объема выборки, соответствующие ошибки получили название ошибок выборочности или ошибок репрезентативности.
Учитывая, что размер этой ошибки является функцией объема выборки, соответствующие ошибки получили название ошибок выборочности или ошибок репрезентативности.
Слайд 17Равенство или неравенство математических ожиданий оценок и соответствующих им констант служит
критерием для определения качества ошибок, которое получило название смещенности.
Слайд 18Требования, предъявляемые к оценкам
Состоятельность
Точечные оценки называют состоятельными, если при увеличении числа
испытаний (n→∞) они стремятся к величине оцениваемых параметров. Для µ - и σ² - Sx²
Несмещенность
Если математические ожидания при любом объеме выборки равны оцениваемому параметру или константе, то такие оценки называют несмещенными.
Слайд 20Если средняя арифметическая вычисляется способом условной средней ее ошибка определяется как:
Слайд 29Вероятности, признанные достаточными, для суждений о генеральных параметрах на основании выборочных
показателей называются доверительными
Р – доверительная вероятность.
При Р=0,95 есть риск ошибиться при оценке генерального параметра 1 раз на 20 испытаний
(Р=0,99 – 1 раз на 100 испытаний, Р=0,999 – 1 раз на 1000 испытаний).
Уровень значимости 0,05; 0,01; 0,001 (вместо Р=0,95)
Каждой доверительной вероятности соответствует своя величина нормированного отклонения t.
Слайд 30
Здесь при Р=0,95 есть риск ошибиться при оценке генерального параметра 1
раз на 20 испытаний
(Р=0,99 – 1 раз на 100 испытаний, Р=0,999 – 1 раз на 1000 испытаний).
Уровень значимости 0,05; 0,01; 0,001 (вместо Р=0,95)
Каждой доверительной вероятности соответствует своя величина нормированного отклонения t.
(Р=0,99 – 1 раз на 100 испытаний, Р=0,999 – 1 раз на 1000 испытаний).
Уровень значимости 0,05; 0,01; 0,001 (вместо Р=0,95)
Каждой доверительной вероятности соответствует своя величина нормированного отклонения t.
Слайд 31Нормированное отклонение – показатель представляющий отклонение той или иной варианты от
средней величины, отнесенное к величине среднего квадратического отклонения.
Слайд 32
Вероятность отклонения любой варианты (хi) нормально распределяющейся совокупности от центра распределения
(μ) определяется функцией и нормированного отклонения (t), и доверительный интервал для неизвестного параметра будет равен:
