- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
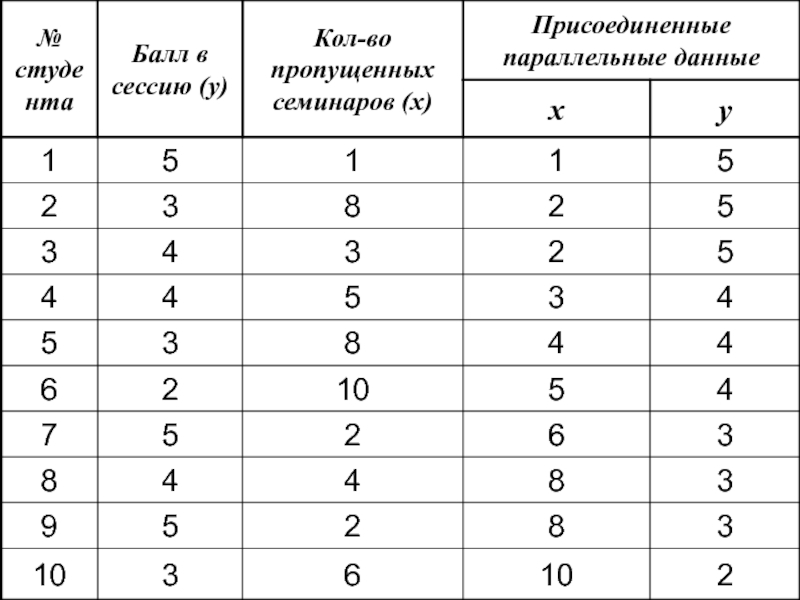
Статистическое изучение взаимосвязи социально - экономических явлений презентация
Содержание
- 1. Статистическое изучение взаимосвязи социально - экономических явлений
- 2. Количественные критерии оценки тесноты связи (по Чеддоку)
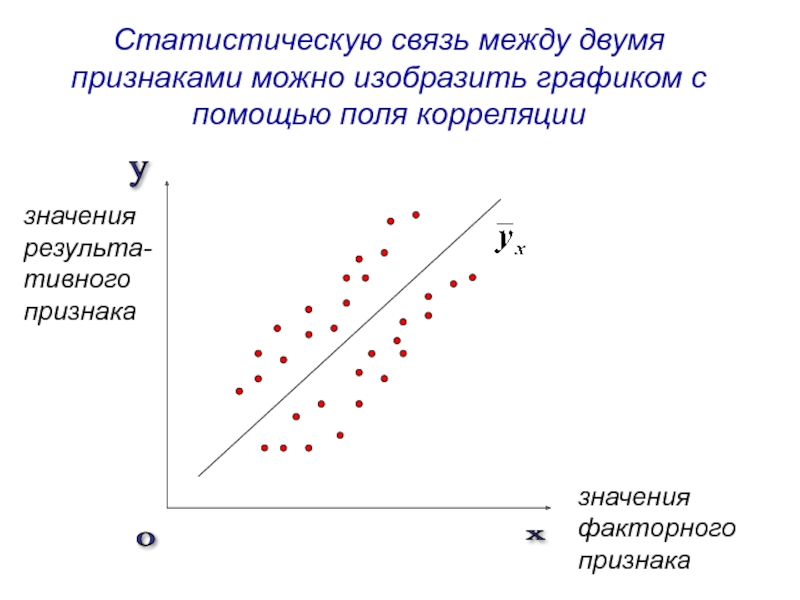
- 4. Статистическую связь между двумя признаками можно изобразить
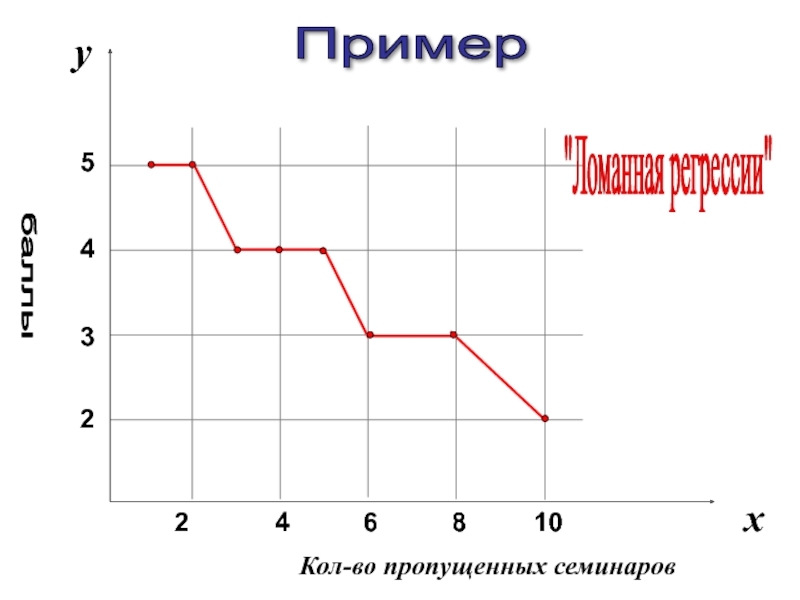
- 5. 2 4 6 8 10 x y
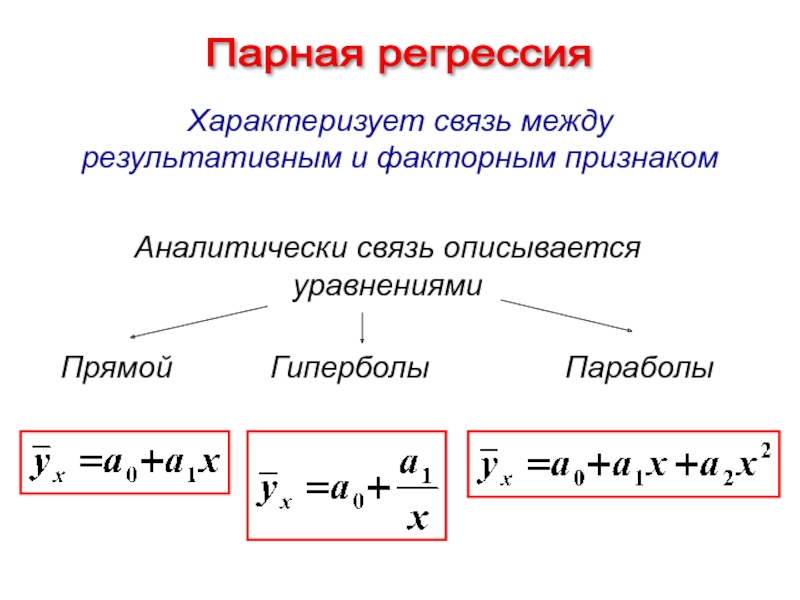
- 6. Парная регрессия Характеризует связь между результативным
- 7. Метод наименьших квадратов Система уравнений для
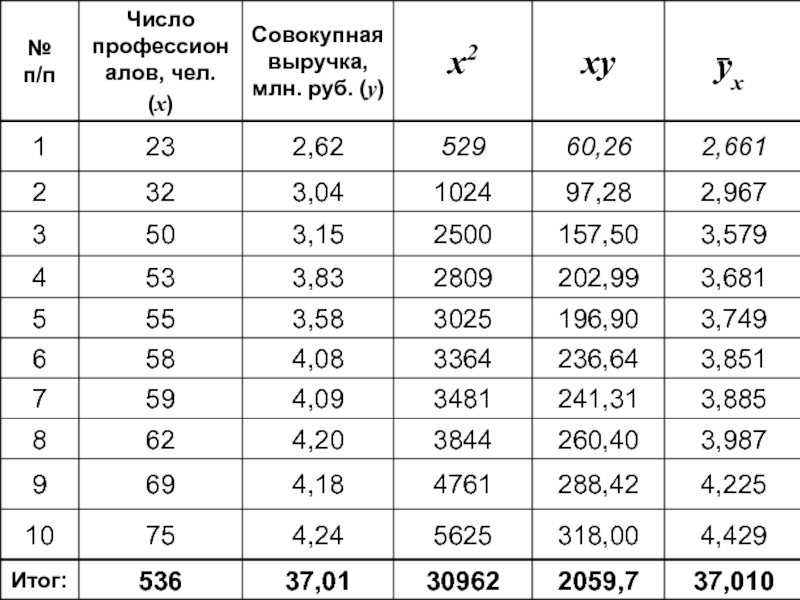
- 9. При увеличении числа профессионалов на 1 человека
- 11. Считая, что зависимость описывается уравнением прямой, коэффициенты а0 и а1 определяются из системы нормальных уравнений:
- 12. Промежуточные расчеты: По 1ой группе:
- 13. Промежуточные расчеты: По 2ой группе:
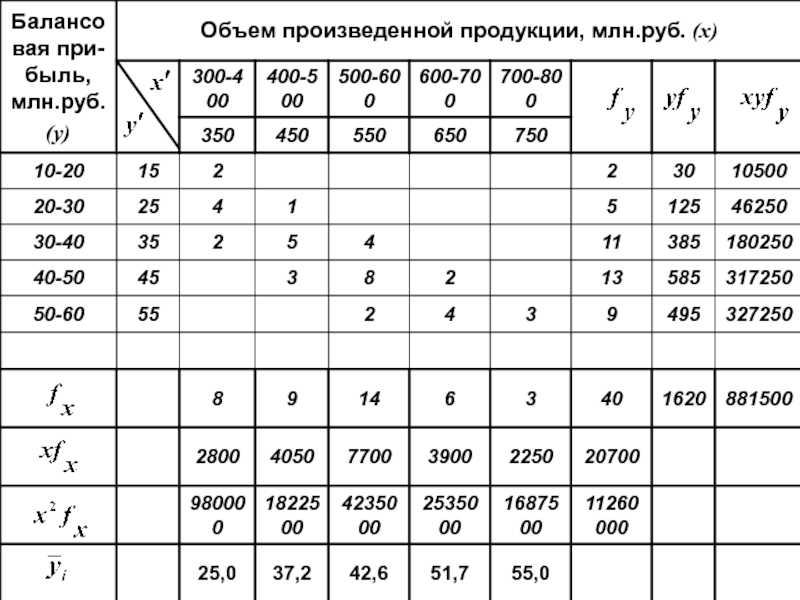
- 14. При увеличении объема выпуска на 1 млн.руб.
- 15. Если связь между признаками криволинейная и описывается
- 16. Оценка обратной зависимости между х и у осуществляется на основании уравнения гиперболы
- 17. Типы моделей Характеризующих зависимости между социально-экономическими движениями - Линейная - Степенная
- 18. Типы моделей - Показательная - Параболическая - Гиперболическая
- 20. Система нормальных уравнений имеет вид:
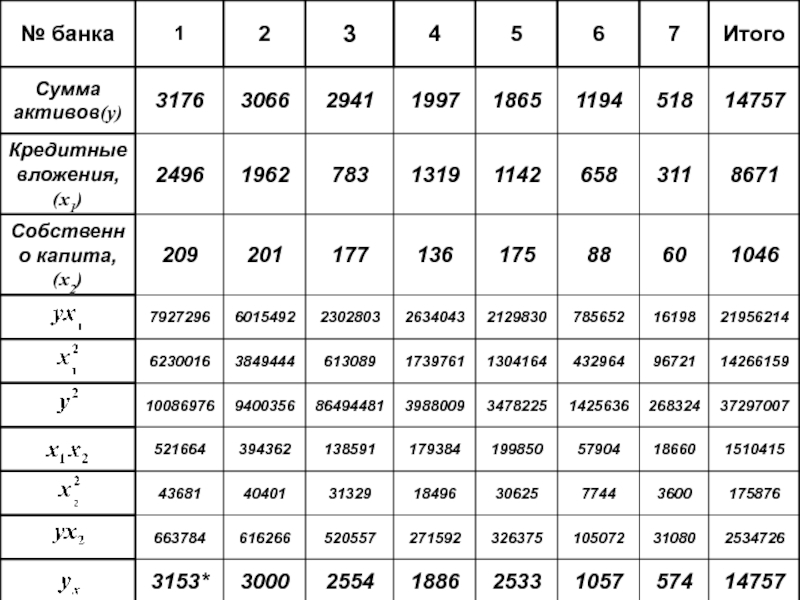
- 21. При увеличении кредитных вложений на 1 млн.руб.
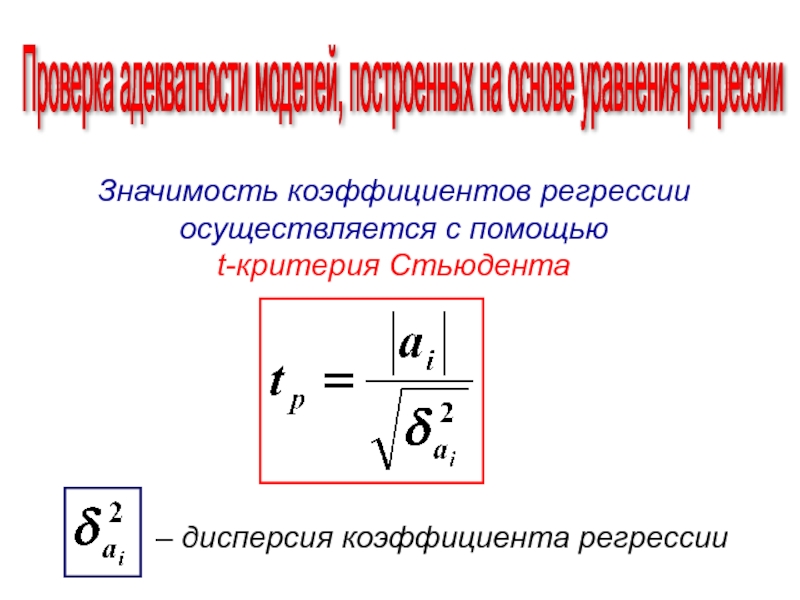
- 22. Проверка адекватности моделей, построенных на основе уравнения
- 23. – уровень значимости проверки гипотезы о равенстве
- 24. Определение дисперсии: – дисперсия результативного признака
- 25. Определение дисперсии: – величина множественного коэффициента
- 26. Если
- 27. Число степеней свободы – число наблюдений n – число факторных признаков в уравнении k
- 28. Значение средней ошибки аппроксимации не должно превышать 12-15%
- 29. Частные коэффициенты эластичности: – среднее значение
- 30. Пример: По данным о сумме актов
- 31. При увеличении кредитных вложений и собственного капитала
- 32. Частный коэффициент детерминации: – парный коэффициент
- 33. Рассчитать частный коэффициент детерминации для фактора
- 34. 3) 4) 5) Пример:
- 35. Пример: 6) 2% вариации стоимости активов объясняется изменением величины кредитных вложений
- 36. Рассчитать частный коэффициент детерминации для фактора
- 37. 3) 4) 5) Пример:
- 38. Пример: 6) На 88% изменение стоимости активов объясняется изменением собственного капитала
- 39. Q-коэффициент: – коэффициент вариации соответствующего факторного
- 40. Рассчитать Qx1 для фактора x1 – кредитного вложения Пример: 1) 2)
- 41. Рассчитать Qx2 для фактора x2 – собственный капитала Пример: 1) 2)
- 42. Линейный коэфициент корреляции Различные модификации ф-ии для расчета данного коэффициента: 1) 2)
- 43. Линейный коэфициент корреляции При изучении совокупностей малого объема: 3) 4) (Через дисперсии слагаемых)
- 44. Зависимость между линейным коэффициентом корреляции и коэфициентом
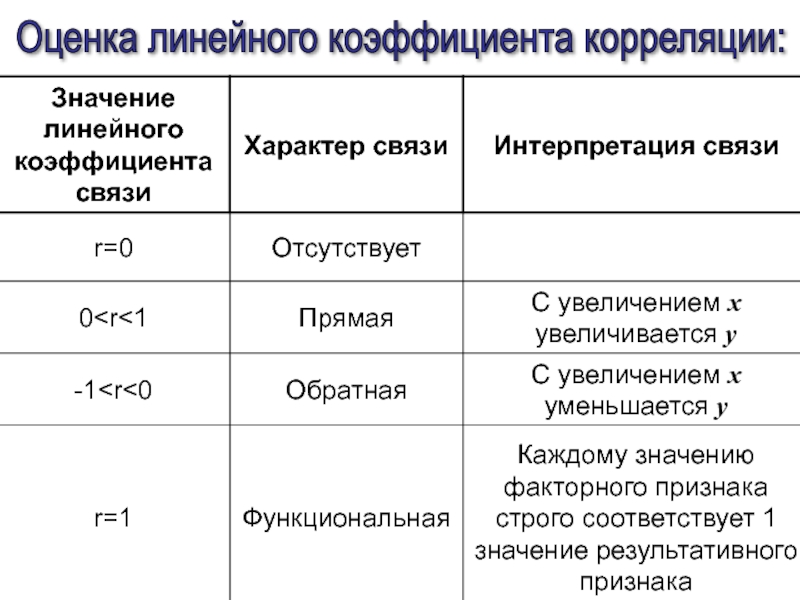
- 45. Оценка линейного коэффициента корреляции:
- 46. Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента при n
- 47. при n>100 Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента
- 48. Оценить тесноту связи между стоимостью активов (y)
- 49. Проверка значимости: Коэффициент корреляции значим
- 50. Эмпирическое корреляционное отношение – общая дисперсия – межгрупповая дисперсия
- 51. Теоритическое корреляционное отношение – дисперсия выровненных
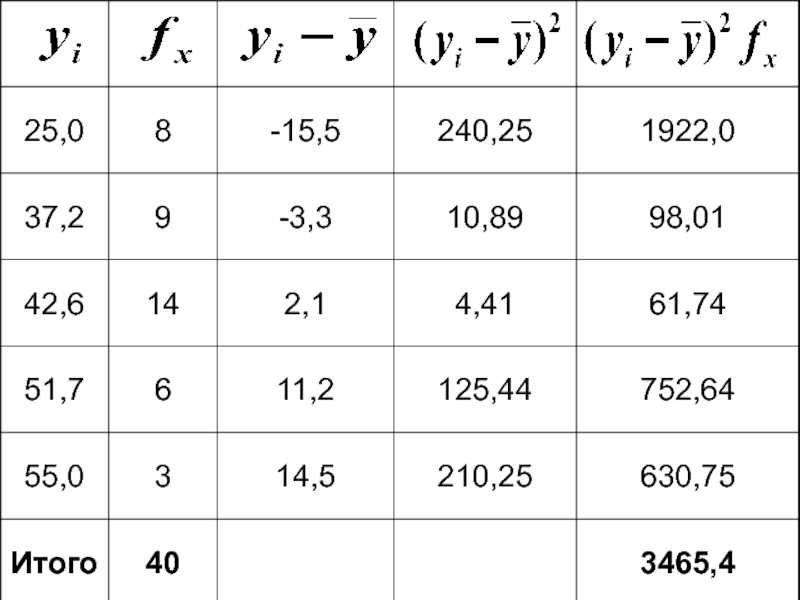
- 52. Пример: По данным группировки 40 предприятий
- 54. Связь сильная
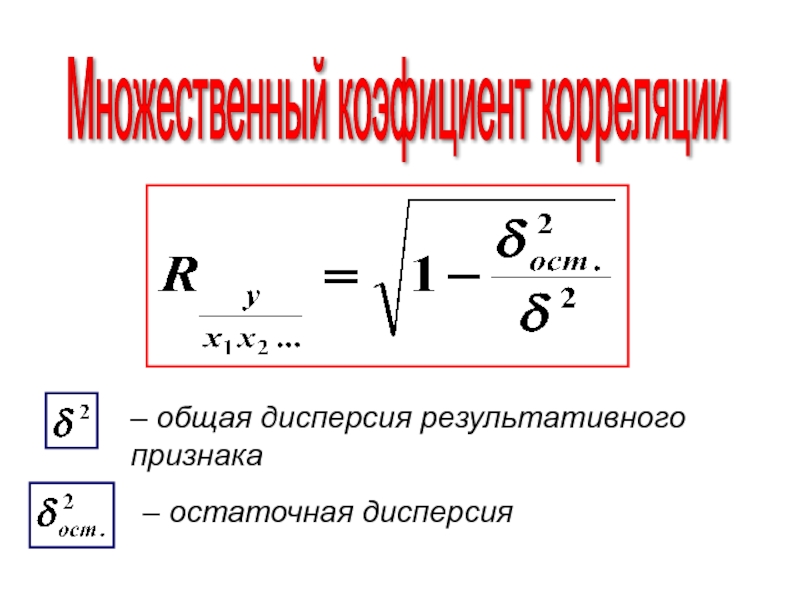
- 55. Множественный коэфициент корреляции – общая дисперсия результативного признака – остаточная дисперсия
- 56. – парные коэффициенты корреляции между признаками
- 57. Используя парные коэффициенты rij и коэффициенты
- 58. – число факторных признаков k
- 59. Проверка значимости коэффициента осуществляется на основании F-критерия Фишера-Снедекора
- 60. Если: Гипотеза о
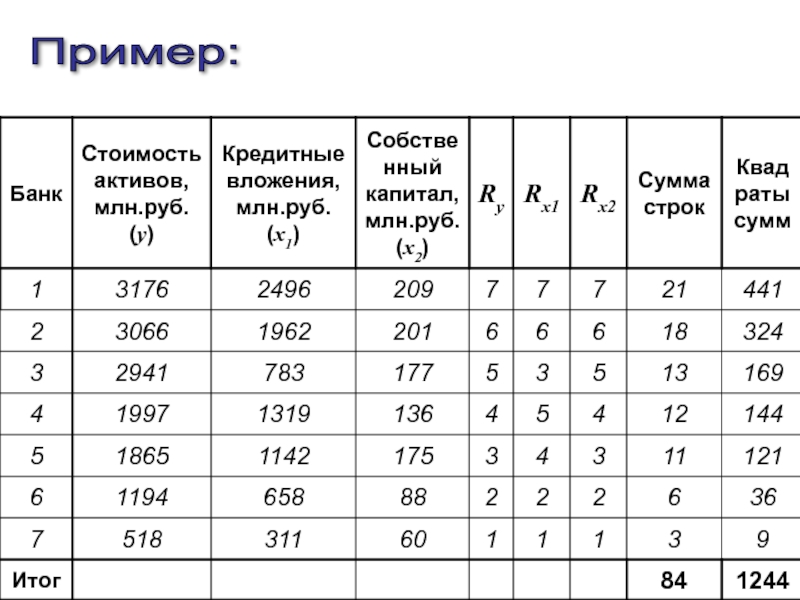
- 61. По данным о сумме актов кредитных вложений
- 62. Связь сильная, факторы x1 и x2 практически полностью обуславливают величину y. 4)
- 63. Гипотеза о незначимости коэффициента отвергается Проверка значимости:
- 64. Коэффициент частной корреляции 1ого порядка
- 65. В случае зависимости y от 2x факторных
- 66. По данным о сумме актов кредитных вложений
- 67. 4) Пример: 5)
- 68. 6) Пример:
- 69. Проверка значимости: 1) 2) 3)
- 70. Проверка значимости: Не все полученные коэффициенты корреляции значимы 4)
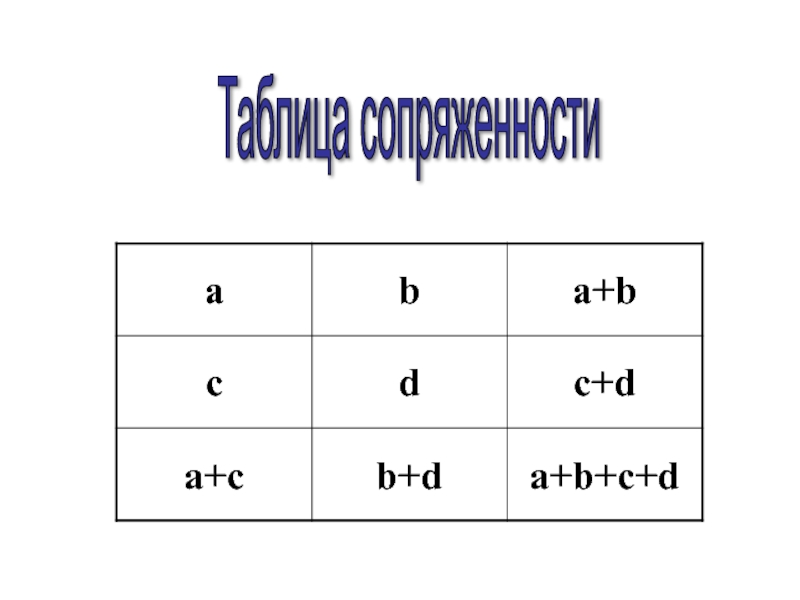
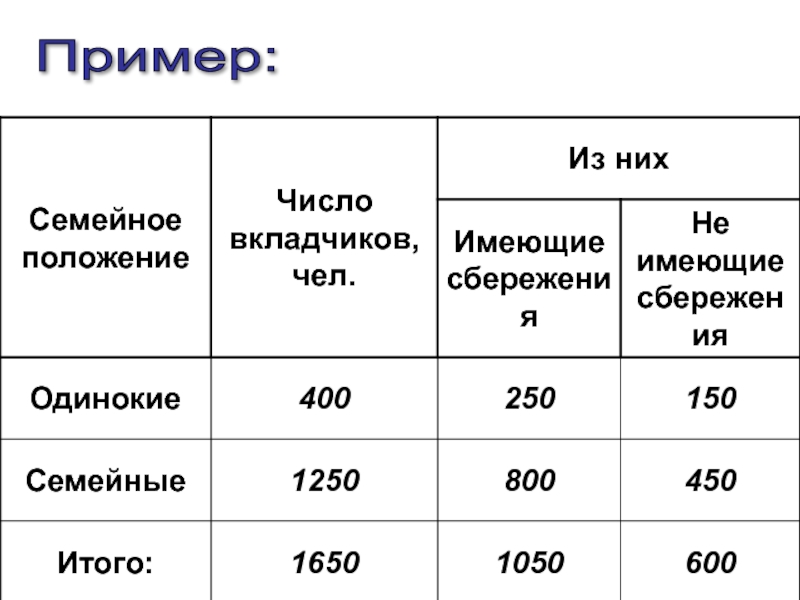
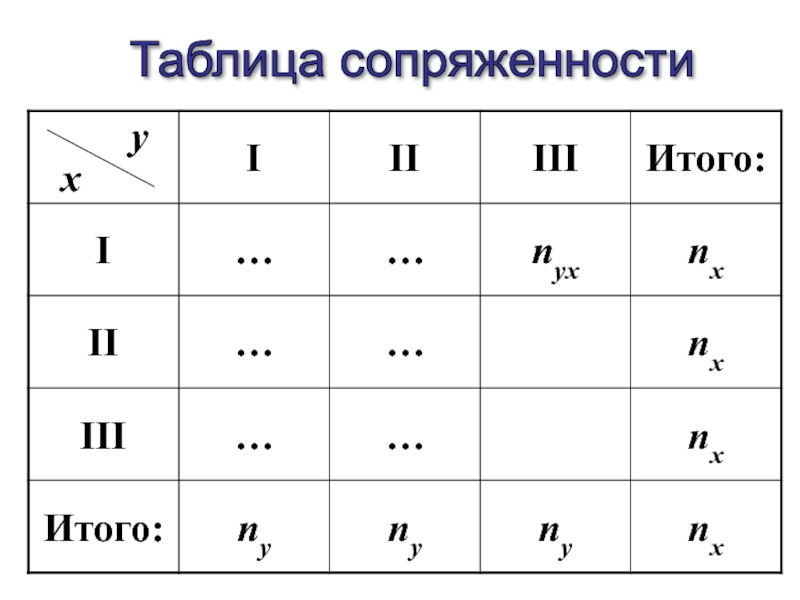
- 71. Таблица сопряженности
- 72. Коэффициенты ассоциации и контингенции Связь считается подтвержденной всегда
- 73. Пример:
- 75. Таблица сопряженности y x
- 76. Коэффициенты взаимной сопряженности Пирсона и Чупрова
- 77. – определяется как сумма отношений квадратов частот
- 78. – число значений (групп) 1ого признака k1 – число значений (групп) 2ого признака k2
- 79. Пример:
- 81. Связь близка к умеренной
- 82. Модификация коэффициента Пирсона -наиболее распространенный критерий
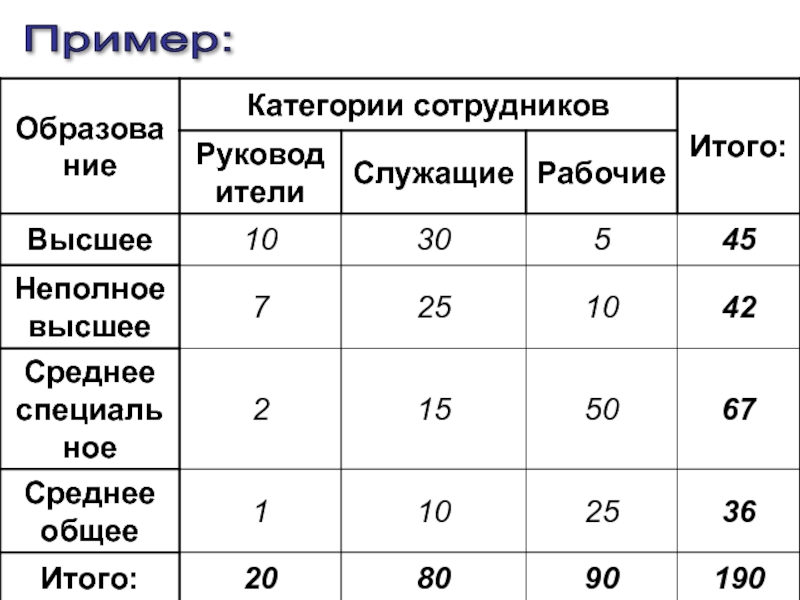
- 83. Пример: (По данным таблицы об уровне образования сотрудников)
- 84. Модификация коэффициента Чупрова – число строк
- 85. Пример: (По данным таблицы об уровне образования сотрудников) Связь средняя
- 86. Бисериальный коэффициент корреляции
- 87. – среднее квадратичное отклонение фактических значений признака
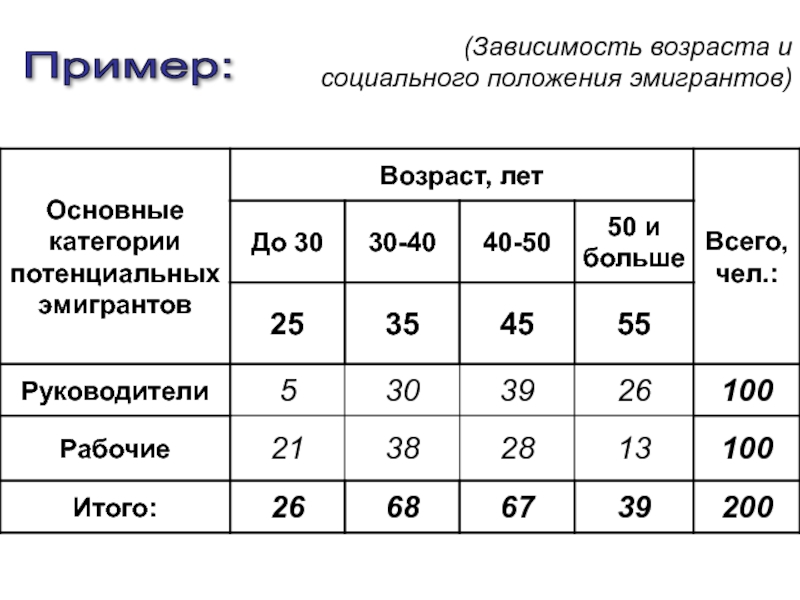
- 88. Пример: (Зависимость возраста и социального положения эмигрантов)
- 90. Связь умеренная
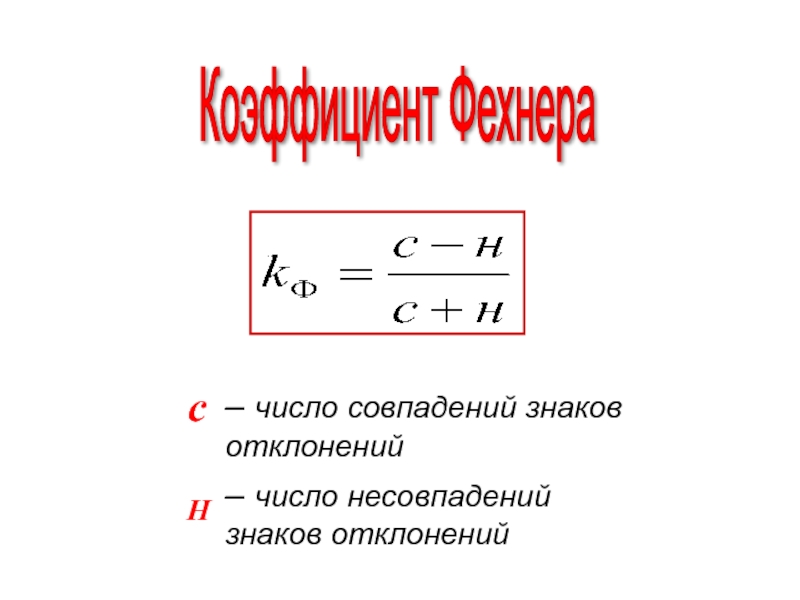
- 91. Коэффициент Фехнера – число совпадений знаков
- 92. – связь между признаками функциональная – связь
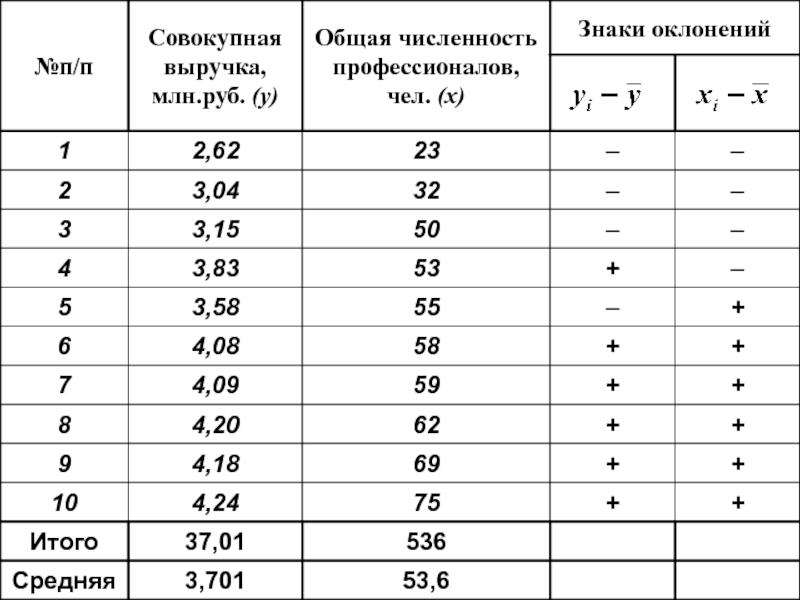
- 94. Связь между совокупной выручкой и численностью профессионалов аудиторско-консультационных фирм прямая и умеренная
- 95. Коэффициент корреляции рангов (Спирмена) – квадрат
- 96. Значимость коэффициента Спирмэна проверяется на основе t-критерия Стьюдента Значение статистически существенно
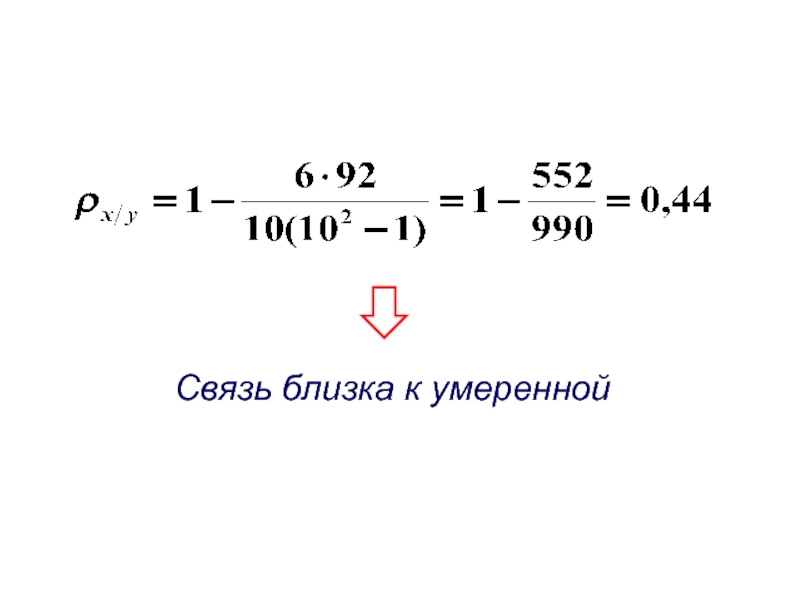
- 98. Связь близка к умеренной
- 99. Коэффициент корреляции рангов (Кенделла) – сумма
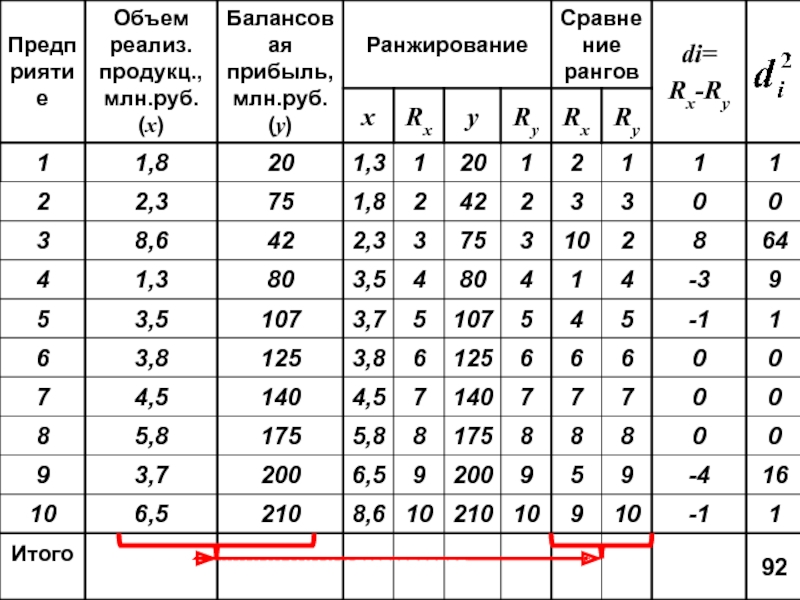
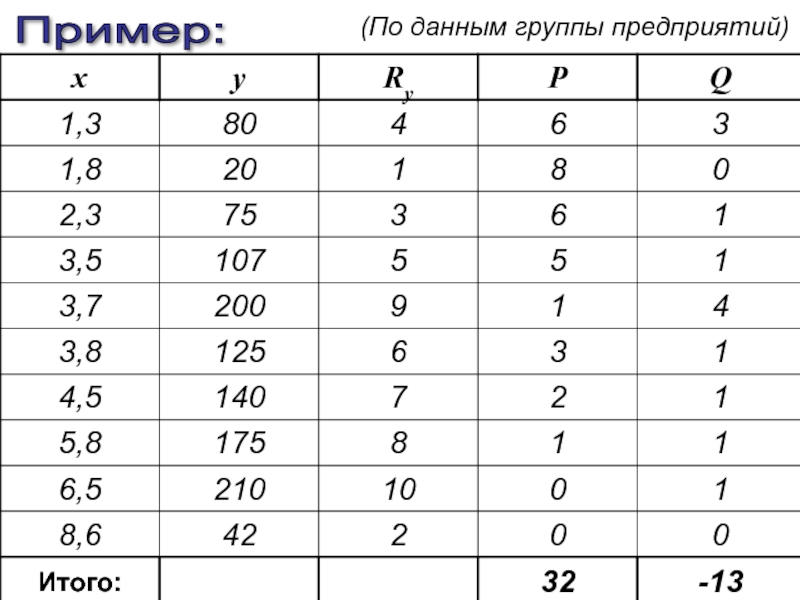
- 100. Пример: (По данным группы предприятий)
- 101. Связь близка к умеренной
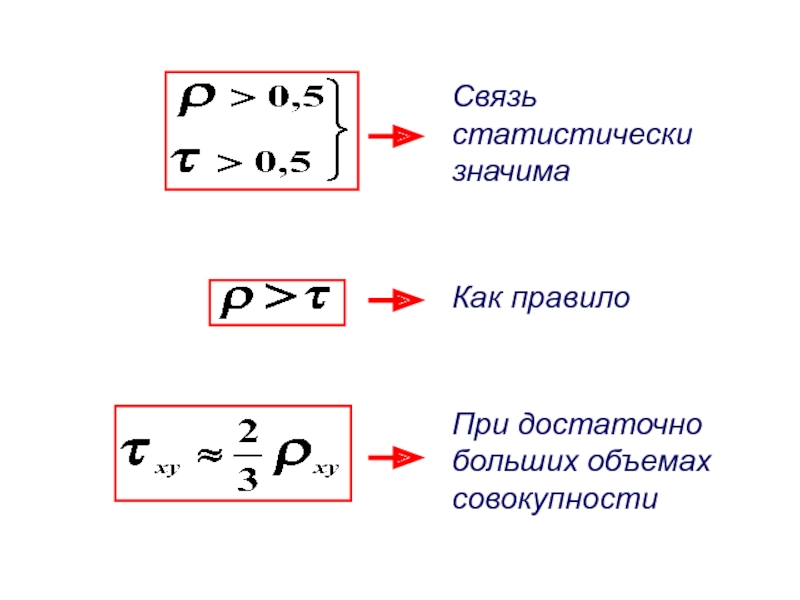
- 102. Как правило Связь статистически значима При достаточно больших объемах совокупности
- 103. Множественный коэффициент корреляции рангов (коэффициент конкордации)
- 104. Значимость коэффициента конкордации проверяется на основе -критерия Пирсона
- 105. Пример:
- 106. По таблице «распределение Пирсона» (
Слайд 4Статистическую связь между двумя признаками можно изобразить графиком с помощью поля
y
x
0
значения факторного признака
значения результа-тивного признака
Слайд 6Парная регрессия
Характеризует связь между результативным и факторным признаком
Аналитически связь описывается
Прямой
Гиперболы
Параболы
Слайд 7Метод наименьших квадратов
Система уравнений для нахождения параметров линейной парной регрессии:
–
n
Слайд 9При увеличении числа профессионалов на 1 человека её совокупная выручка увеличивается
Слайд 11Считая, что зависимость описывается уравнением прямой, коэффициенты а0 и а1 определяются
Слайд 14При увеличении объема выпуска на 1 млн.руб. балансовая прибыль в среднем
Слайд 15Если связь между признаками криволинейная и описывается уравнением параболы 2ого порядка,
Слайд 17Типы моделей
Характеризующих зависимости между социально-экономическими движениями
- Линейная
- Степенная
Слайд 21При увеличении кредитных вложений на 1 млн.руб. и собственного капитала коммерческих
Слайд 22Проверка адекватности моделей, построенных на основе уравнения регрессии
– дисперсия коэффициента
Значимость коэффициентов регрессии осуществляется с помощью
t-критерия Стьюдента
Слайд 23– уровень значимости проверки гипотезы о равенстве нулю параметров, измеряющих связь
Параметр
статистически значимым, если
– число степеней свободы, которое характеризует число свободно варьирующих элементов совокупности
Слайд 24Определение дисперсии:
– дисперсия результативного признака
- простой способ
– число факторных
Слайд 25Определение дисперсии:
– величина множественного коэффициента корреляции по фактору xi с
- более точная оценка
Слайд 26Если
То – гипотеза о несоответствии заложенных в уравнение регрессии связей реально существующим отвергается
Слайд 29Частные коэффициенты эластичности:
– среднее значение соответствующего факторного признака
– среднее значение
– коэффициент регрессии при соответствующем факторном признаке
Слайд 30Пример:
По данным о сумме актов (y) кредитных вложений (x1) и
Слайд 31При увеличении кредитных вложений и собственного капитала на 1% стоимость актов
на 0,02 и 1,19%
Слайд 32Частный коэффициент детерминации:
– парный коэффициент корреляции между результативным и i-ным
– соответственный коэффициент уравнения множественной регрессии в стандартизированном масштабе
Слайд 33Рассчитать частный коэффициент детерминации для
фактора x1 – кредитного вложения
1)
2)
Пример:
Слайд 36Рассчитать частный коэффициент детерминации для
фактора x2 – собственный капитал
2)
1)
Пример:
Слайд 39Q-коэффициент:
– коэффициент вариации соответствующего факторного признака
– используется для более точной
Слайд 42Линейный коэфициент корреляции
Различные модификации ф-ии для расчета данного коэффициента:
1)
2)
Слайд 43Линейный коэфициент корреляции
При изучении совокупностей малого объема:
3)
4)
(Через дисперсии слагаемых)
Слайд 44Зависимость между линейным коэффициентом корреляции и коэфициентом регрессии
– среднее квадратичное
– коэффициент регрессии в уравнении связи
Слайд 47при n>100
Значимость линейного коэффициента корреляции проверяется
на основе t-критерия Стьюдента
Слайд 51Теоритическое корреляционное отношение
– дисперсия выровненных значений результативного признака
– дисперсия эмпирических
Слайд 52Пример:
По данным группировки 40 предприятий легкой промышленности по величине балансовой
Слайд 55Множественный коэфициент корреляции
– общая дисперсия результативного признака
– остаточная дисперсия
Слайд 56– парные коэффициенты корреляции между признаками
r
В случае оценки связи
Слайд 57 Используя парные коэффициенты rij и коэффициенты регрессии в стандартизированном масштабе
Слайд 58– число факторных признаков
k
Чтобы оценить общую вариацию результативности
– число наблюдений
n
Не корректируется, если:
Слайд 61По данным о сумме актов кредитных вложений и величине собственного капитала
1)
Пример:
2)
3)
Слайд 65В случае зависимости y от 2x факторных признаков:
– парные коэффициенты корреляции
r
Слайд 66По данным о сумме актов кредитных вложений и величине собственного капитала
1)
Пример:
2)
3)
Слайд 77– определяется как сумма отношений квадратов частот каждой клетки таблицы к
Показатель взаимной сопряженности
Слайд 82Модификация коэффициента Пирсона
-наиболее распространенный критерий согласия, используемый для проверки статистической
Слайд 84Модификация коэффициента Чупрова
– число строк в таблице
k1
– число граф в
k2
– число наблюдений
n
Слайд 87– среднее квадратичное отклонение фактических значений признака от среднего уровня
– доля
– табулированные значения z-распределения в зависимости от p
– средние в группах
и
– доля второй группы
Слайд 91Коэффициент Фехнера
– число совпадений знаков отклонений
c
Н
– число несовпадений знаков
Слайд 92– связь между признаками функциональная
– связь отсутствует
– связь обратная, с увеличением/снижением
– связь прямая, с увеличением/снижением х увеличивается/снижается у
Слайд 94Связь между совокупной выручкой и численностью профессионалов аудиторско-консультационных фирм прямая и
Слайд 95Коэффициент корреляции рангов (Спирмена)
– квадрат разности рангов
di
n
– число наблюдений
(число
2
Слайд 96Значимость коэффициента Спирмэна проверяется
на основе t-критерия Стьюдента
Значение статистически существенно
Слайд 99Коэффициент корреляции рангов (Кенделла)
– сумма разностей между числом последовательностей и
S
n
– число наблюдений
Слайд 103Множественный коэффициент корреляции рангов (коэффициент конкордации)
– количество факторов
m
S
– отклонение суммы
n
– число наблюдений