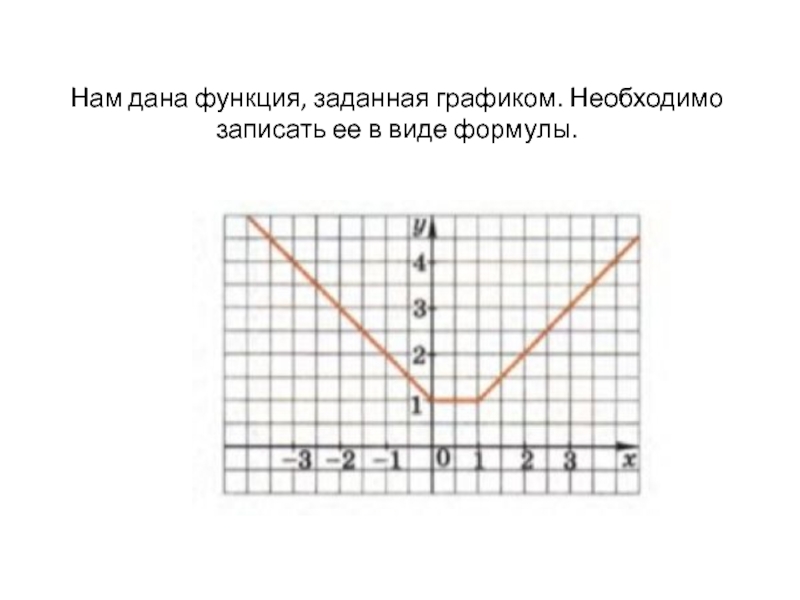
Прежде чем приступить к изучению связи между явлениями необходимо выяснить вид связи между факторным и результативным признаками.
Различают два вида связи:
1- Функциональная связь
когда каждому значению величины факторного признака соответствует только одно значение результативного.
При этом зависимость проявляется с одинаковой силой у всех единиц совокупности. Ее можно представить уравнением
у = f (x),
где у – результативный признак, x – факторный, f (x) – известная функция