- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистические оценки параметров распределения случайных величин по выборкам. Вариационные ряды и их графики презентация
Содержание
- 1. Статистические оценки параметров распределения случайных величин по выборкам. Вариационные ряды и их графики
- 2. Вариационные ряды и их графики дают наглядное
- 3. К числу важнейших показателей, используемых в статистическом
- 4. В зависимости от того, как распределены первичные
- 5. Средние величины. В отличие от индивидуальных числовых
- 6. Показатели средних величин обладают следующими свойствами: являются
- 7. средние величины могут характеризовать только однородную совокупность
- 8. Структурные средние и способы их вычисления. Структурные
- 9. При нормальном распределении величины моды (Mo), медианы
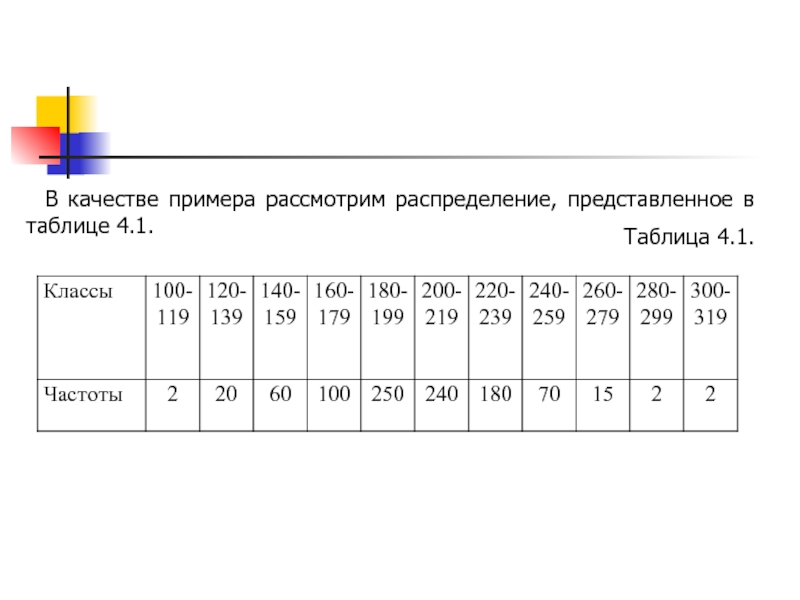
- 10. В качестве примера рассмотрим распределение, представленное в таблице 4.1. Таблица 4.1.
- 11. В этом распределении наиболее многочисленным является пятый
Слайд 1Тема лекции 4.
Статистические оценки параметров распределения случайных величин по выборкам.
Слайд 2Вариационные ряды и их графики дают наглядное представление о варьировании признаков,
Слайд 3К числу важнейших показателей, используемых в статистическом анализе, относят:
1) средние
2) показатели разнообразия и
3) показатели соответствия выборочных данных параметрам генеральной совокупности.
Слайд 4В зависимости от того, как распределены первичные данные – в равно-
Слайд 5Средние величины. В отличие от индивидуальных числовых характеристик средние величины обладают
Различают структурные (мода, медиана) и степенные (средняя арифметическая, средняя взвешенная и др.) средние.
Слайд 6Показатели средних величин обладают следующими свойствами:
являются обобщенными статистическими параметрами, они позволяют
средняя – это величина абстрактная, т.к. при ее вычислении можно получать такие дробные значения, которые в действительности не могут иметь место в связи с природой самого признака;
средняя величина имеет конкретное выражение, показывая величину признака в том же наименовании, в котором он измерялся;
Слайд 7средние величины могут характеризовать только однородную совокупность вариант;
одни средние применяются только
Слайд 8Структурные средние и способы их вычисления. Структурные величины представляют собой конкретные
Мода (Мо) – это наиболее часто встречающаяся варианта в вариационном ряду. Мода отличается полной независимостью от крайних значений. Для малых выборок мода не определяется.
Слайд 9При нормальном распределении величины моды (Mo), медианы (Ме) и средней арифметической
. Чем больше асимметрия ряда, тем больше разница между Мо, Ме,
Моду применяют для характеристики не только количественных, но и качественных признаков, что важно при изучении генетических особенностей альтернативных признаков.
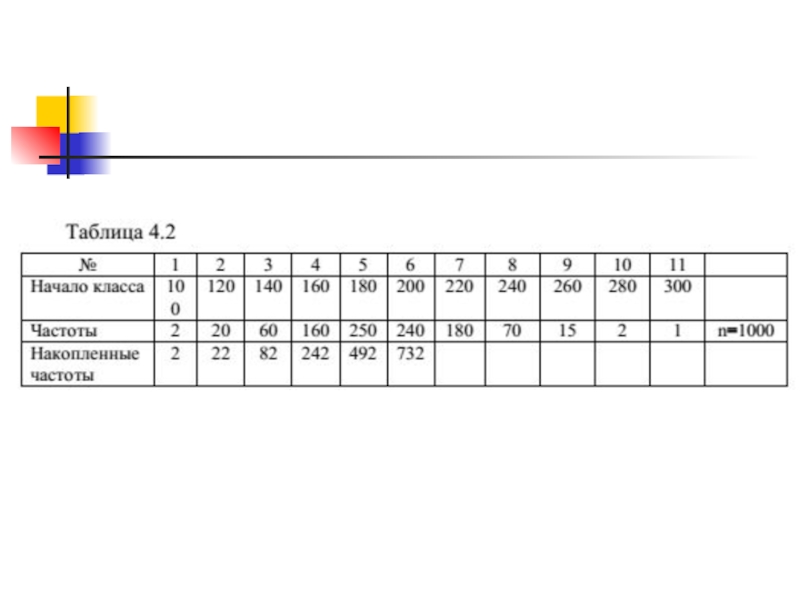
Слайд 11В этом распределении наиболее многочисленным является пятый класс (180-199 с частотой
Формула для вычисления моды (Мо):
Мо = ХМо + k
где:
ХМо – варианта, соответствующая началу модального класса;
k – классный промежуток;
f1 – частота, предшествующая модальному классу;
f2 – частота модального класса;
f3 – частота, следующая за модальным классом.
[2],