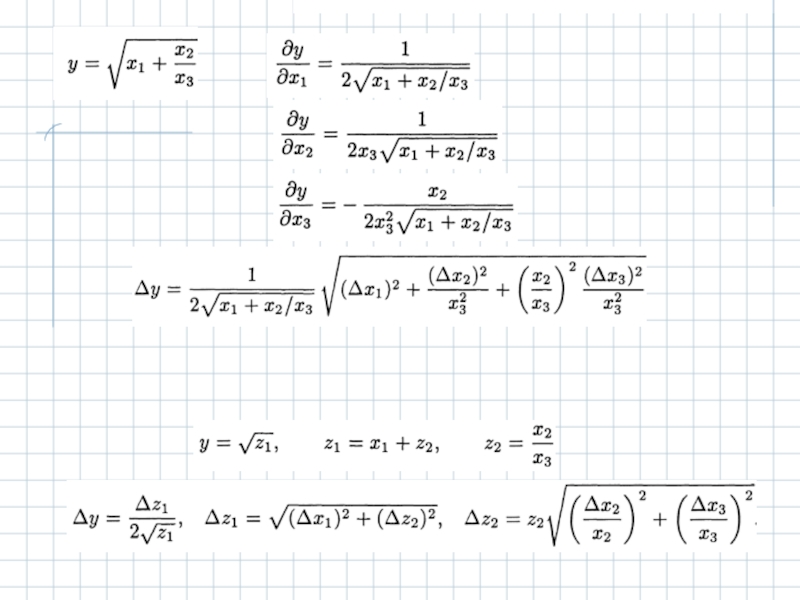отклонения от среднего)
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Статистическая обработка результатов эксперимента презентация
Содержание
- 1. Статистическая обработка результатов эксперимента
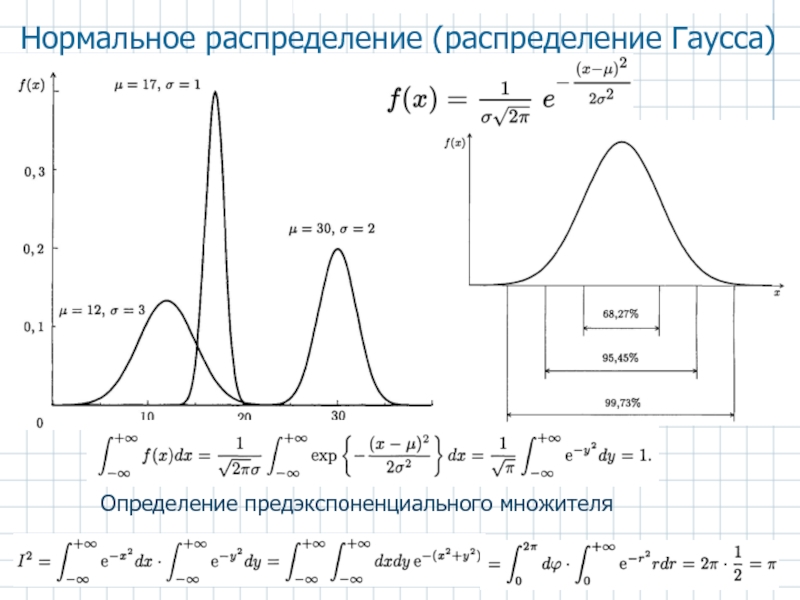
- 2. Определение предэкспоненциального множителя Нормальное распределение (распределение Гаусса)
- 3. Другие виды распределений: - Биноминальное (дискретное) -
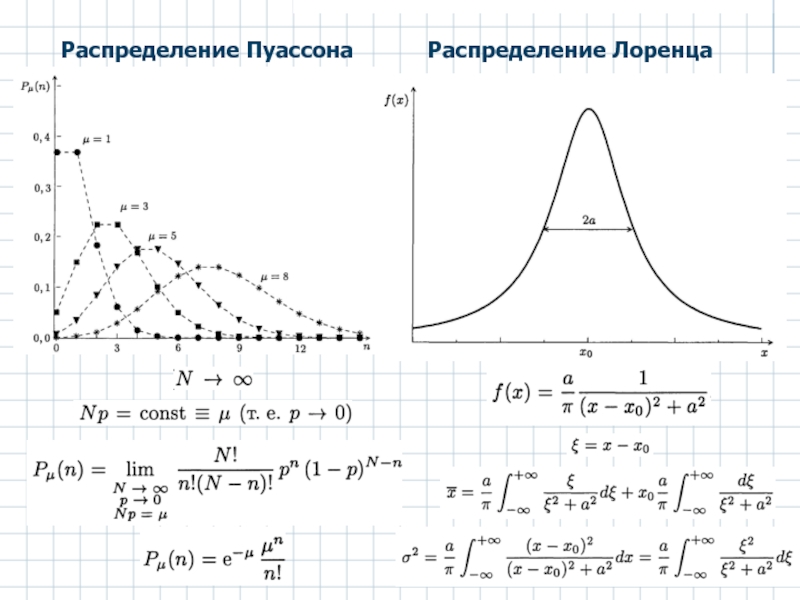
- 4. Распределение Пуассона Распределение Лоренца
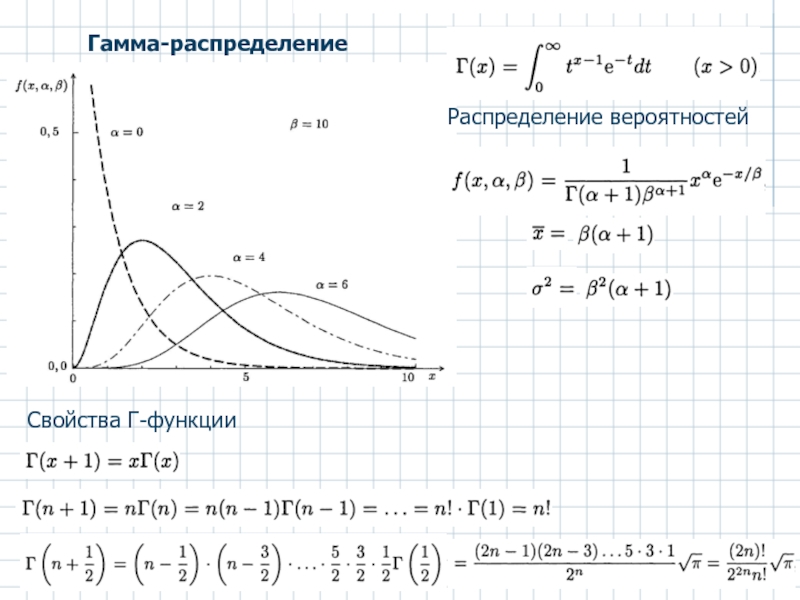
- 5. Гамма-распределение Свойства Г-функции Распределение вероятностей
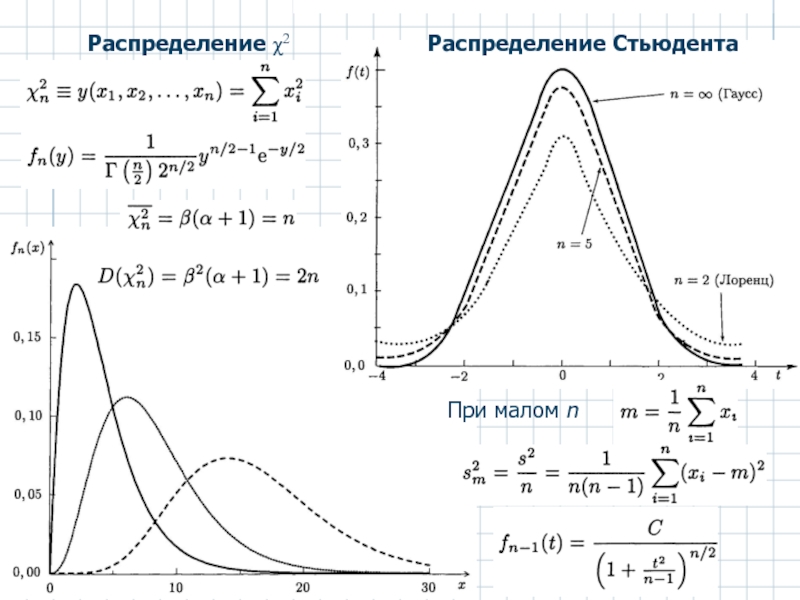
- 6. Распределение χ2 Распределение Стьюдента При малом n
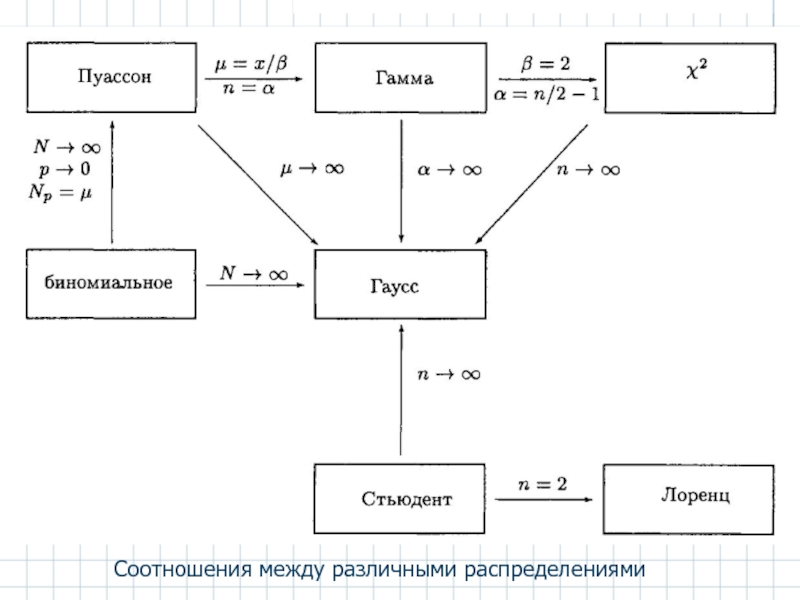
- 7. Соотношения между различными распределениями
- 9. Статистическая обработка результатов эксперимента Если в
- 11. Правила округления 1. Точность результатов измерений и
- 12. Распространение ошибок
- 14. Косвенные измерения
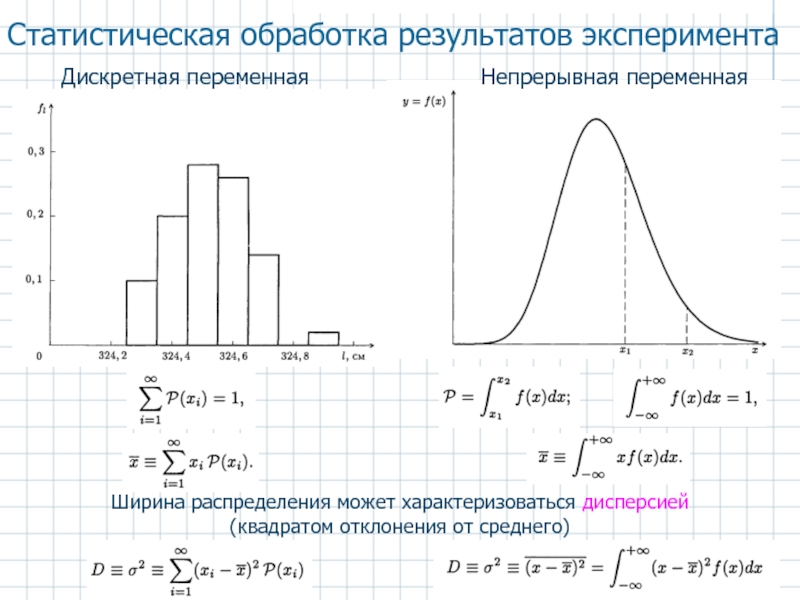
Слайд 1Статистическая обработка результатов эксперимента
Дискретная переменная
Непрерывная переменная
Ширина распределения может характеризоваться дисперсией
(квадратом
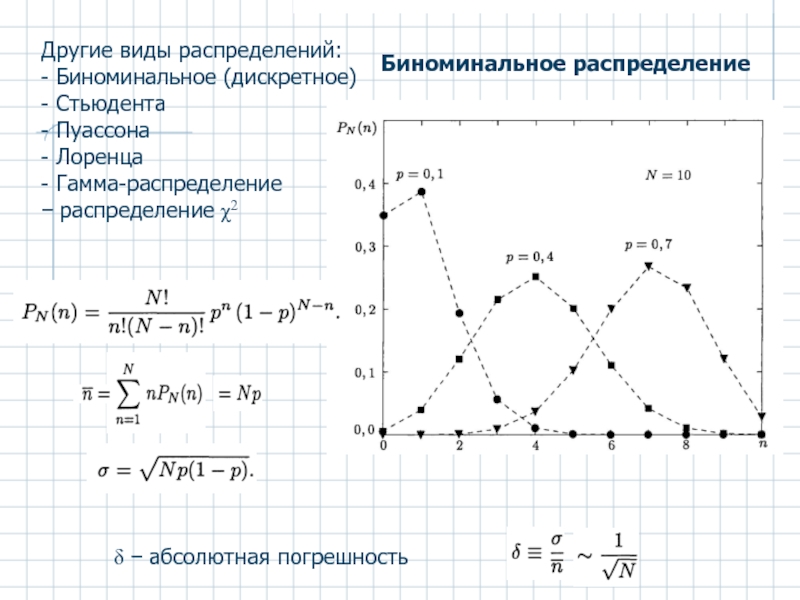
Слайд 3Другие виды распределений:
- Биноминальное (дискретное)
- Стьюдента
- Пуассона
- Лоренца
- Гамма-распределение
− распределение χ2
Биноминальное
распределение
δ − абсолютная погрешность
Слайд 9Статистическая обработка результатов эксперимента
Если в результате измерения n раз некоторой
физической величины x получен ряд значений x1, x2, ..., xn, то в качестве значения, наиболее близкого к истинному, принимается среднее арифметическое
Случайную ошибку измерений оценивают по среднеквадратичному отклонению от среднего значения измеряемой величины x.
Истинное значение измеренной величины x лежит в интервале от до
, где Δx называется доверительным интервалом. Вероятность этого события (доверительная вероятность) составляет P.
Доверительный интервал рассчитывается по формуле
где tP,n-1 - коэффициент Стьюдента, зависящий от доверительной вероятности P и числа измерений n.
Таким образом, окончательная форма записи результата имеет вид
Случайную ошибку измерений оценивают по среднеквадратичному отклонению от среднего значения измеряемой величины x.
Истинное значение измеренной величины x лежит в интервале от до
, где Δx называется доверительным интервалом. Вероятность этого события (доверительная вероятность) составляет P.
Доверительный интервал рассчитывается по формуле
где tP,n-1 - коэффициент Стьюдента, зависящий от доверительной вероятности P и числа измерений n.
Таким образом, окончательная форма записи результата имеет вид
Слайд 11Правила округления
1. Точность результатов измерений и точность вычислений при обработке результатов
измерений должны быть согласованы с требуемой точностью получаемой оценки измеряемой величины.
2. Погрешность оценки измеряемой величины следует выражать не более чем двумя значащими цифрами.
Две значащие цифры в погрешности оценки измеряемой величины сохраняют:
- при точных измерениях;
- если первая значащая цифра не более трех.
3. Сохраняемую значащую цифру в погрешности оценки измеряемой величины при округлении увеличивают на единицу, если отбрасываемая цифра неуказываемого младшего разряда больше либо равна пяти, и не изменяют, если она меньше пяти.
2. Погрешность оценки измеряемой величины следует выражать не более чем двумя значащими цифрами.
Две значащие цифры в погрешности оценки измеряемой величины сохраняют:
- при точных измерениях;
- если первая значащая цифра не более трех.
3. Сохраняемую значащую цифру в погрешности оценки измеряемой величины при округлении увеличивают на единицу, если отбрасываемая цифра неуказываемого младшего разряда больше либо равна пяти, и не изменяют, если она меньше пяти.