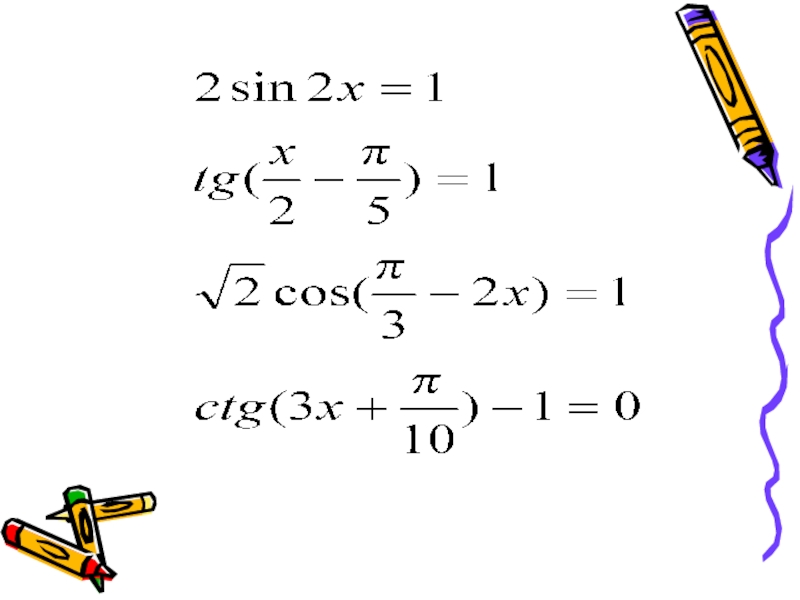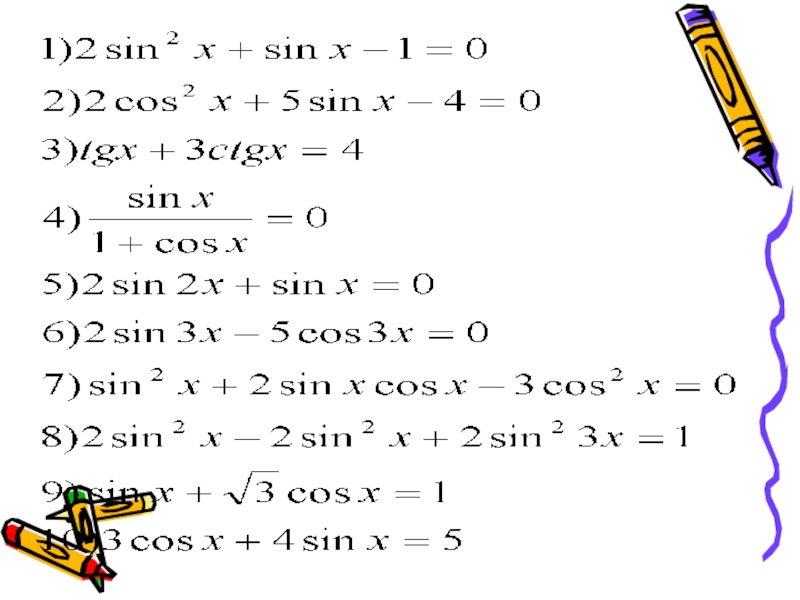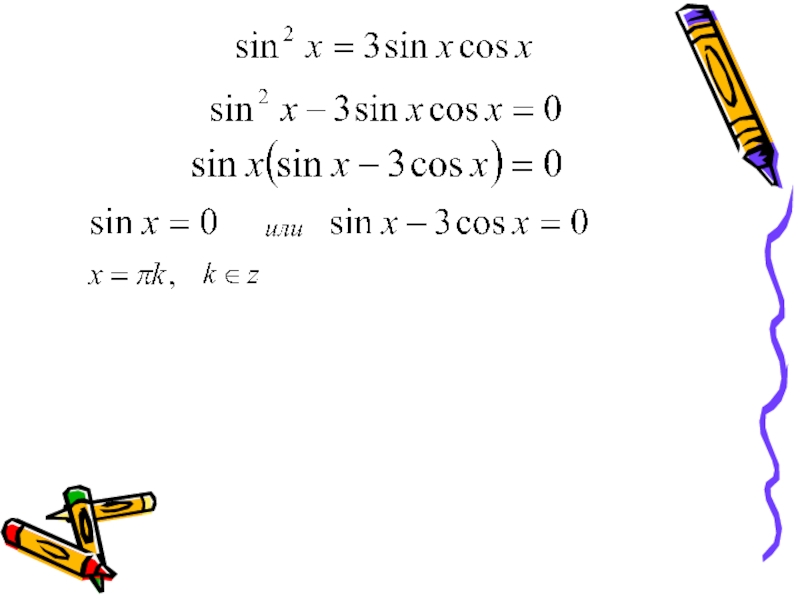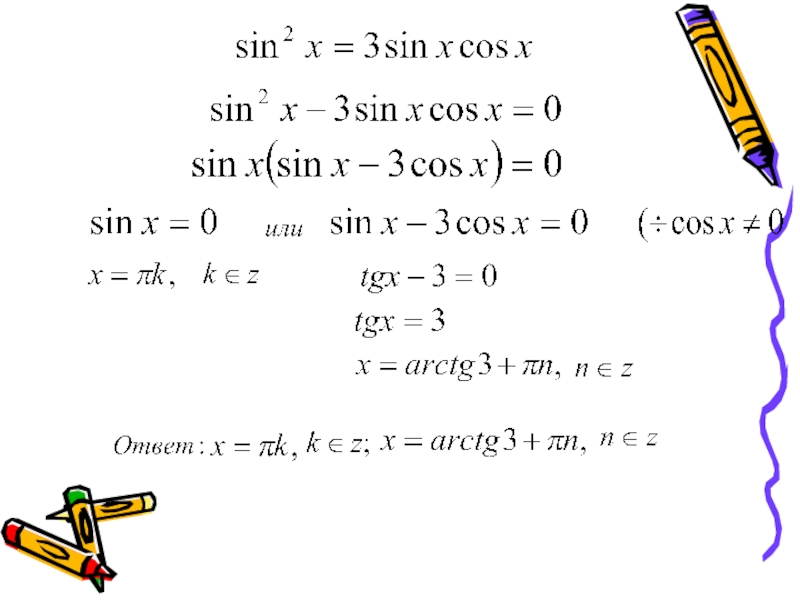- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Способы решения тригонометрических уравнений презентация
Содержание
- 1. Способы решения тригонометрических уравнений
- 2. Знать: Свойства тригонометрических функций. Определения обратных тригонометрических
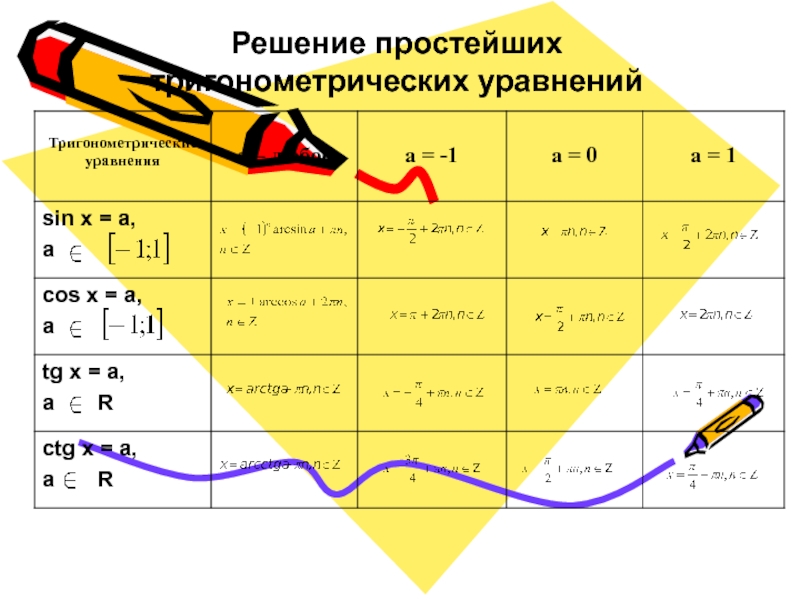
- 3. Решение простейших тригонометрических уравнений
- 6. Методы решения тригонометрических уравнений Разложение на множители
- 7. Знать: Способы решения тригонометрических уравнений: сведения к
- 8. Лейбниц «Метод решения хорош, если с самого
- 9. Сведения к квадратному уравнению Пусть a = sin x Ответ:
- 10. Сведения к квадратному уравнению Пусть
- 11. Сведения к квадратному уравнению Пусть
- 12. Алгоритм решения тригонометрических уравнений. Привести уравнение
- 13. Разложения на множители Ответ:
- 15. Однородные уравнения Первой степени: a∙sinx
- 17. Однородные уравнения
- 18. Пусть a = tg x Ответ: Однородные уравнения
- 19. Метод понижения степени
- 20. Метод понижения степени Ответ: Метод понижения степени
- 21. Метод понижения степени Ответ:
- 22. Метод введения вспомогательного угла >0
- 23. Метод введения вспомогательного угла
- 24. Правила. Увидел квадрат – понижай степень.
- 25. Проблемы, возникающие при решении тригонометрических уравнений.
- 26. 1.Потеря корней: делим на
- 27. Можно ли насладиться решением уравнения sinx+cosx=1? Да, если стать его исследователем!
- 28. 1 способ: Введение вспомогательного аргумента
- 29. 2 способ: Применение универсальной подстановки
- 30. «Мне приходится делить время между политикой и
Знать: Свойства тригонометрических функций. Определения обратных тригонометрических функций. Формулы тригонометрии. Формулы решения простейших тригонометрических уравнений. Уметь: Вычислять значения тригонометрических функций. Вычислять значения обратных тригонометрических функций. Решать простейшие тригонометрические уравнения.
Слайд 2Знать:
Свойства тригонометрических функций.
Определения обратных тригонометрических функций.
Формулы тригонометрии.
Формулы решения простейших тригонометрических уравнений.
Уметь:
Вычислять
значения тригонометрических функций.
Вычислять значения обратных тригонометрических функций.
Решать простейшие тригонометрические уравнения.
Выполнять тождественные преобразования выражений.
Вычислять значения обратных тригонометрических функций.
Решать простейшие тригонометрические уравнения.
Выполнять тождественные преобразования выражений.
Слайд 6Методы решения тригонометрических уравнений
Разложение на множители
Сведение к алгебраическому уравнению
Введение вспомогательного угла
Универсальная
подстановка
Сведение к однородному уравнению
Использование формул преобразования суммы в произведение и обратно
Применение формул понижения степени
Обращение к условию равенства одноименных тригонометрических функций
Использование свойства ограниченности функций (метод оценки)
Сведение к однородному уравнению
Использование формул преобразования суммы в произведение и обратно
Применение формул понижения степени
Обращение к условию равенства одноименных тригонометрических функций
Использование свойства ограниченности функций (метод оценки)
Слайд 7Знать:
Способы решения тригонометрических уравнений:
сведения к квадратному уравнению
разложения на множители
понижения степени.
однородные
уравнения
введения вспомогательного угла.
введения вспомогательного угла.
Уметь:
Классифицировать тригонометрические уравнения по способу решения.
Решать тригонометрические уравнения следующими способами:
способом сведения к квадратному уравнению
способом разложения на множители
способом понижения степени.
однородные уравнения.
способом введения вспомогательного угла.
Слайд 8Лейбниц
«Метод решения хорош, если с самого начала мы можем предвидеть –
и впоследствии подтвердить это, - что, следуя этому методу, мы достигнем цели.»
Слайд 12Алгоритм
решения тригонометрических уравнений.
Привести уравнение к квадратному, относительно тригонометрических функций, применяя
тригонометрические тождества.
Ввести новую переменную.
Записать данное уравнение, используя эту переменную.
Найти корни полученного квадратного уравнения.
Перейти от новой переменной к первоначальной.
Решить простейшие тригонометрические уравнения.
Записать ответ.
Ввести новую переменную.
Записать данное уравнение, используя эту переменную.
Найти корни полученного квадратного уравнения.
Перейти от новой переменной к первоначальной.
Решить простейшие тригонометрические уравнения.
Записать ответ.
Слайд 15Однородные уравнения
Первой степени:
a∙sinx + b∙cosx = 0
Т.к. sinx и
cosx одновременно не равны нулю, то разделим обе части уравнения на cosx (или на sinx). Получим: простое уравнение a∙tgx + b = 0 или tgx = m.
Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x. Получим квадратное уравнение:
a∙tg²x + b∙tgx + c = 0.
Слайд 24Правила.
Увидел квадрат – понижай степень.
Увидел произведение – делай сумму.
Увидел сумму
– делай произведение.
Слайд 261.Потеря корней:
делим на g(х).
опасные формулы (универсальная подстановка).
Этими операциями мы
сужаем область определения.
2. Лишние корни:
возводим в четную степень.
умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.
2. Лишние корни:
возводим в четную степень.
умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.
Слайд 30«Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему,
гораздо важнее.
Политика существует только для данного момента, а уравнения будут существовать вечно.»
Политика существует только для данного момента, а уравнения будут существовать вечно.»
А. Эйнштейн
