- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Смежные и вертикальные углы. (7 класс) презентация
Содержание
- 1. Смежные и вертикальные углы. (7 класс)
- 2. План Определение смежных углов Построение смежных углов
- 3. Определение смежных углов Определение. Два угла называются
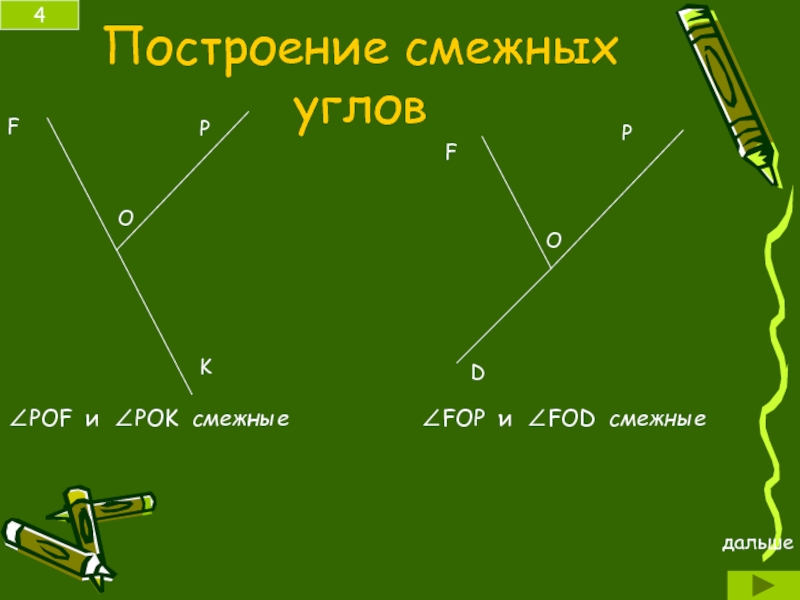
- 4. Построение смежных углов
- 5. Cвойство смежных углов 1. Сколько углов изображено
- 6. Пример оформления решения задачи Один из смежных
- 7. Вертикальные углы Определение. Два угла называются вертикальными,
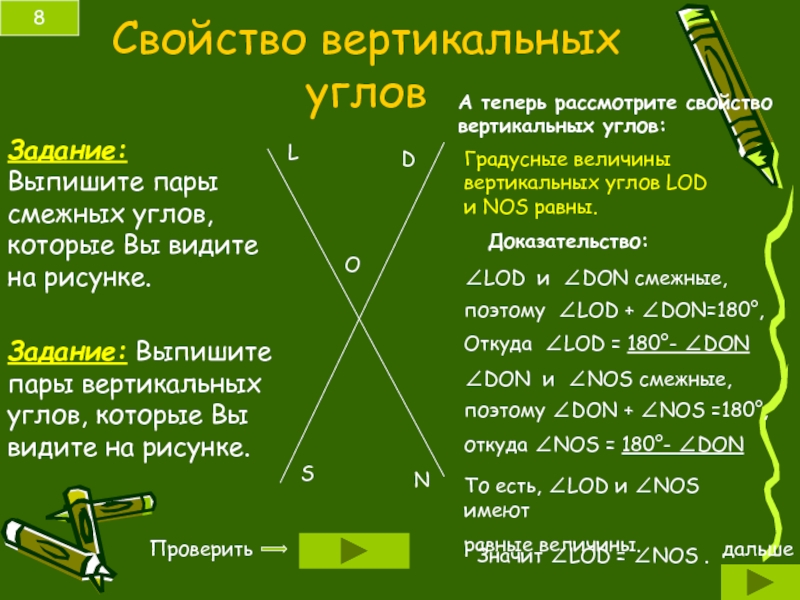
- 8. Свойство вертикальных углов Задание: Выпишите пары
- 9. Построение вертикальных углов Ученику предложили только с
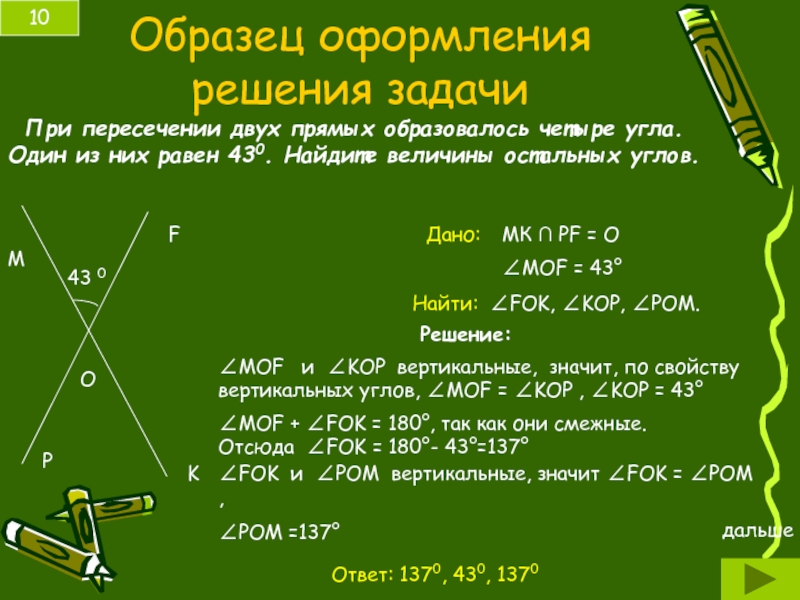
- 10. Образец оформления решения задачи 10 При пересечении
- 11. Обучающая самостоятельная работа 2. Начертите угол МОК.
- 12. 12 назад Порешаем?
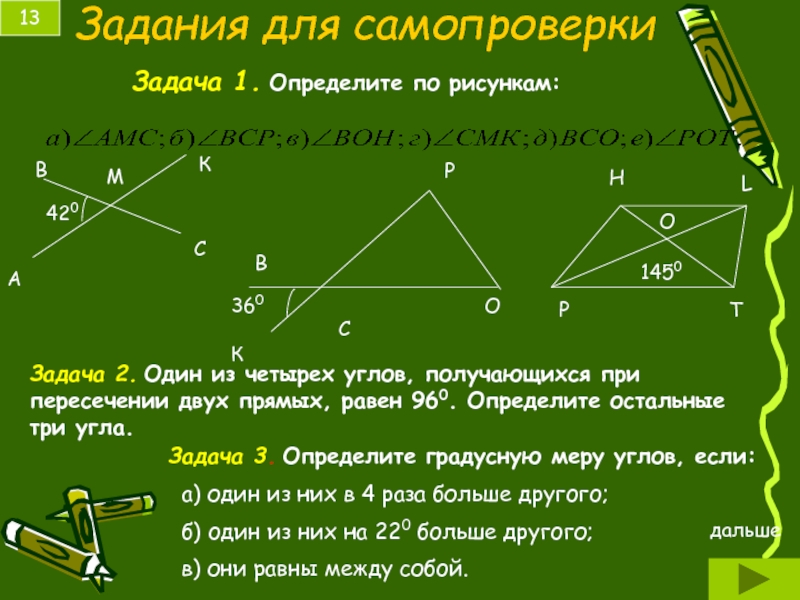
- 13. Задания для самопроверки 13 Задача 1.
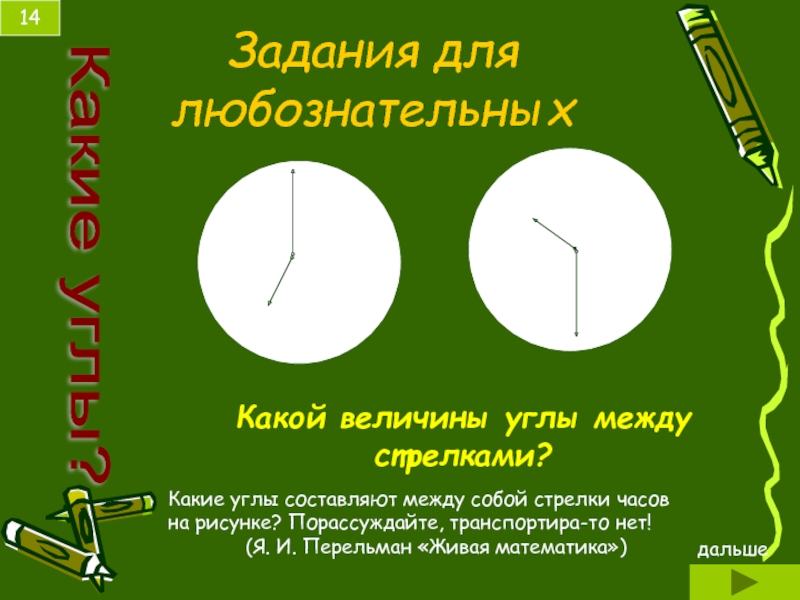
- 14. Задания для любознательных 14 Какие углы? Какой
- 15. 15 Домашнее задание
- 16. Козьма Прутков Отыщи сему начало, и ты многое поймешь 16
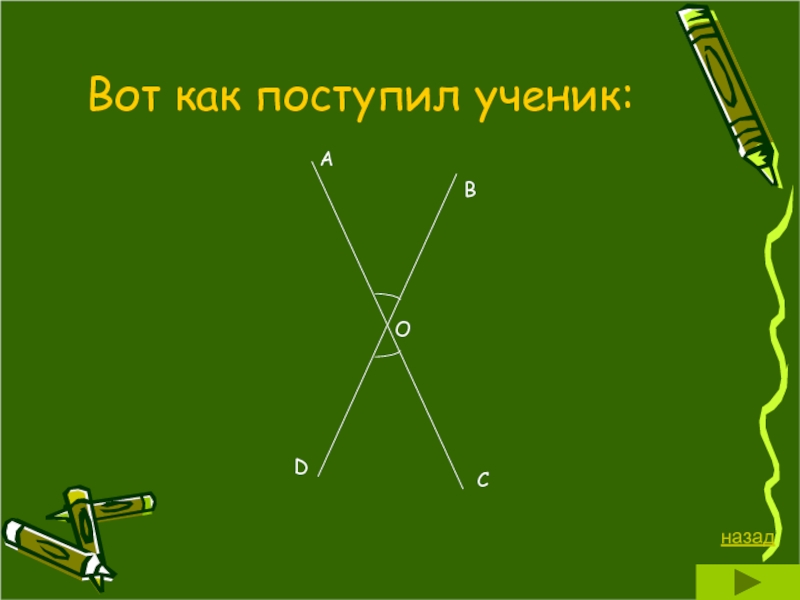
- 17. О Вот как поступил ученик:
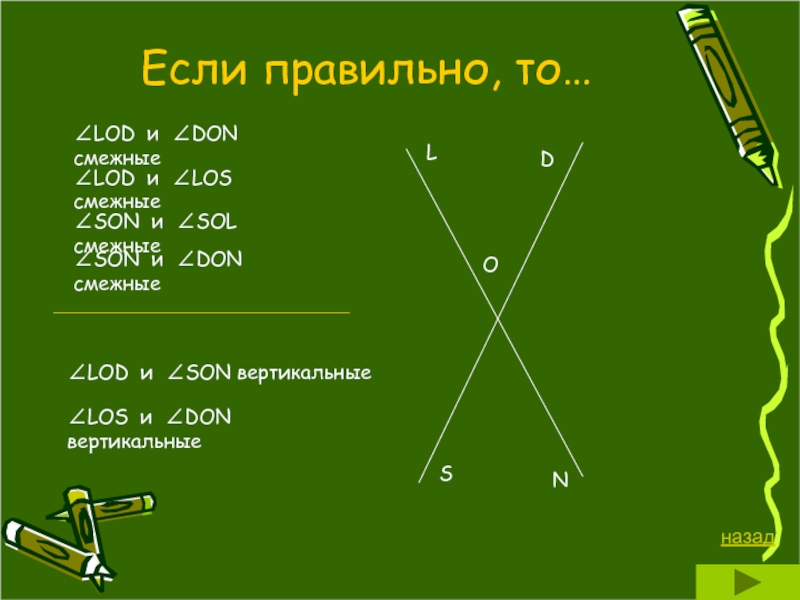
- 18. Если правильно, то…
Слайд 2План
Определение смежных углов
Построение смежных углов
Свойство смежных углов
Пример оформления задачи
Вертикальные углы
Свойство вертикальных
Построение вертикальных углов
Пример оформления задачи
Приложения
Домашнее задание
2
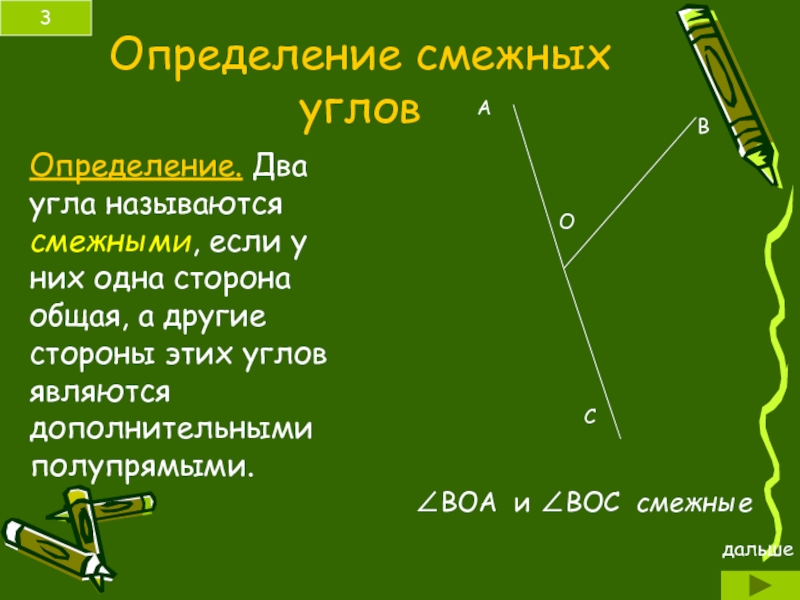
Слайд 3Определение смежных углов
Определение. Два угла называются смежными, если у них одна
3
∠ВОА и ∠ВОС смежные
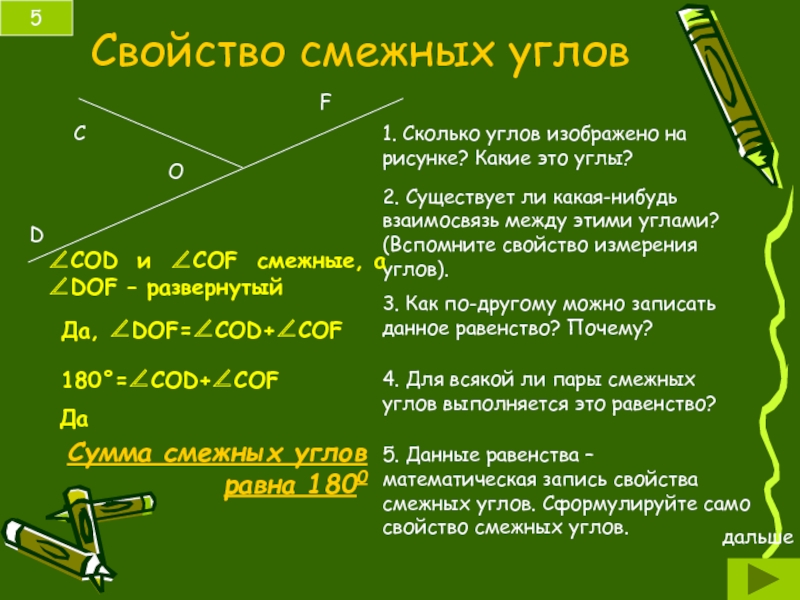
Слайд 5Cвойство смежных углов
1. Сколько углов изображено на рисунке? Какие это углы?
2.
3. Как по-другому можно записать данное равенство? Почему?
4. Для всякой ли пары смежных углов выполняется это равенство?
5. Данные равенства – математическая запись свойства смежных углов. Сформулируйте само свойство смежных углов.
Да
Сумма смежных углов равна 1800
5
∠СOD и ∠COF смежные, а
∠DOF – развернутый
Да, ∠DOF=∠COD+∠COF
180°=∠СOD+∠COF
Слайд 6Пример оформления решения задачи
Один из смежных углов на 320 больше другого.
Решение:
6
Ответ: 740, 1060
∠KOM и ∠KON смежные,
∠KOM - ∠KON = 32°.
Дано:
Найти:
∠KOM , ∠KON .
Пусть ∠КОN = x, тогда ∠КОM = x+32°.
По свойству смежных углов: ∠KOM + ∠KON = 180°.
Значит, х +32°+х =180°,
2х = 180°- 32°,
2х = 148°,
х = 148°:2,
х = 74°.
∠КОN = 74°, тогда ∠КОM = 74° +32°=106°.
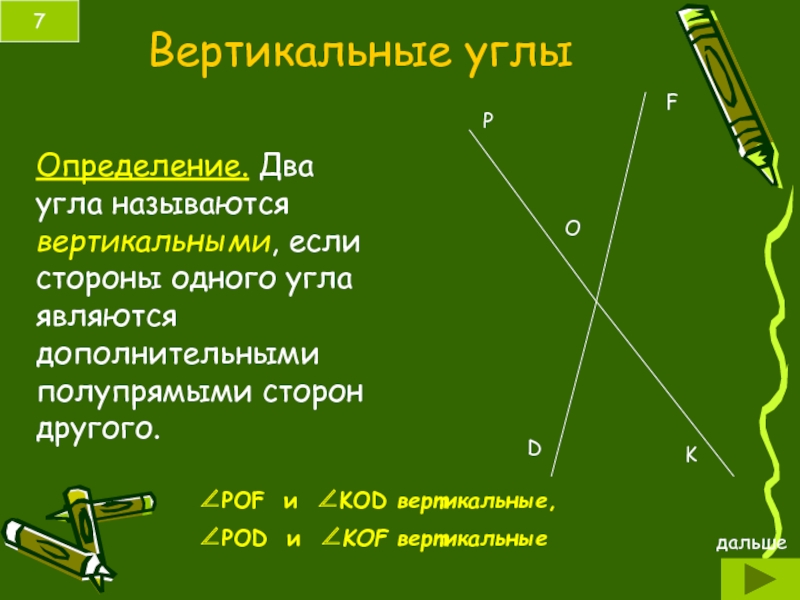
Слайд 7Вертикальные углы
Определение. Два угла называются вертикальными, если стороны одного угла являются
7
∠POF и ∠KOD вертикальные,
∠POD и ∠KOF вертикальные
Слайд 8Свойство вертикальных углов
Задание: Выпишите пары смежных углов, которые Вы видите на
Задание: Выпишите пары вертикальных углов, которые Вы видите на рисунке.
8
А теперь рассмотрите свойство вертикальных углов:
Градусные величины вертикальных углов LOD и NOS равны.
Доказательство:
Слайд 9Построение вертикальных углов
Ученику предложили только с помощью линейки и карандаша построить
9
Слайд 10Образец оформления решения задачи
10
При пересечении двух прямых образовалось четыре угла. Один
Дано:
Найти:
Решение:
Ответ: 1370, 430, 1370
МК ∩ PF = О
∠МОF = 43°
∠FOK, ∠KOP, ∠POM.
Слайд 11Обучающая самостоятельная работа
2. Начертите угол МОК. Постройте смежный с ним: а)
3. Запишите пары смежных углов, имеющиеся на рисунке:
4. Запишите пары вертикальных углов, имеющиеся на рисунке:
11
Слайд 13Задания для самопроверки
13
Задача 1. Определите по рисункам:
Задача 2. Один из четырех
Задача 3. Определите градусную меру углов, если:
а) один из них в 4 раза больше другого;
б) один из них на 220 больше другого;
в) они равны между собой.
Слайд 14Задания для любознательных
14
Какие углы?
Какой величины углы между стрелками?
Какие углы составляют между
(Я. И. Перельман «Живая математика»)