- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Случайные величины. Определение случайной величины (лекция 6) презентация
Содержание
- 1. Случайные величины. Определение случайной величины (лекция 6)
- 2. Определение случайной величины Случайная величина – это
- 3. Дискретная случайная величина и способы ее задания
- 4. Дискретная случайная величина и способы ее задания
- 5. Числовые характеристики дискретной случайной величины Математическое ожидание
- 6. Основные законы распределения дискретных случайных величин Формула
- 7. Основные законы распределения дискретных случайных величин Формулу
- 8. Основные законы распределения дискретных случайных величин При
- 9. Непрерывная случайная величина. Способы ее задания Непрерывной
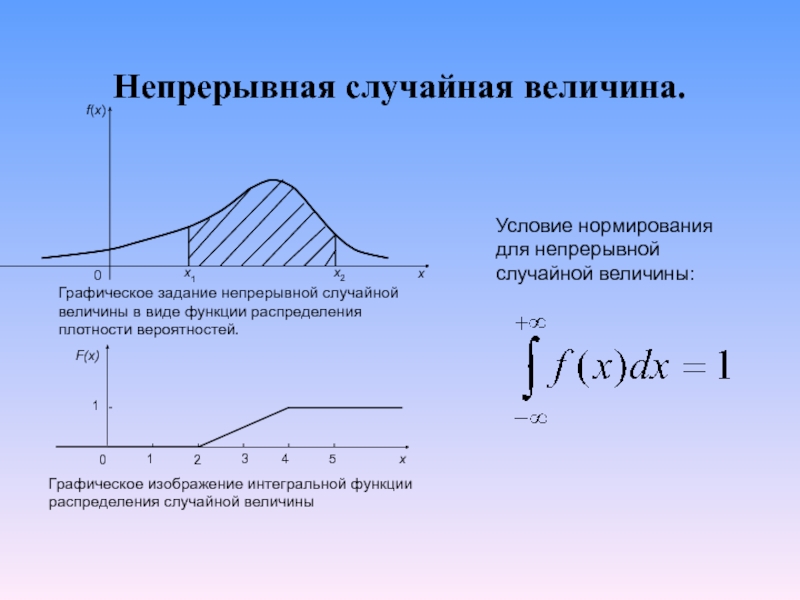
- 10. Непрерывная случайная величина. Условие нормирования для непрерывной случайной величины:
- 11. Числовые характеристики непрерывной дискретной случайной величины Математическое
- 12. Основные законы распределения непрерывных случайных величин 1.
- 13. Основные законы распределения непрерывных случайных величин 2.
- 14. Основные законы распределения непрерывных случайных величин 3.
- 15. Стандартная функция Лапласа Если в функции Гаусса
- 16. Основные законы распределения непрерывных случайных величин 3.
Слайд 2Определение случайной величины
Случайная величина – это величина, принимающая в результате испытания
Различают дискретные и непрерывные случайные величины.
Слайд 3Дискретная случайная величина и способы ее задания
Дискретной случайной величиной называется
Для определения дискретной случайной величины задают закон ее распределения (ряд распре-деления), то есть все возможные значения случайной величины и соответствующие им вероятности:
Слайд 4Дискретная случайная величина и способы ее задания
События, заключающиеся в том, что
Слайд 5Числовые характеристики дискретной случайной величины
Математическое ожидание
Дисперсия
, где
Среднее квадратичное отклонение
Слайд 6Основные законы распределения дискретных случайных величин
Формула Бернулли:
Совокупность полученных вероятностей Рn(0),
Слайд 7Основные законы распределения дискретных случайных величин
Формулу Муавра-Лапласа используют для схемы Бернулли,
Вероятности определяют по формулам:
а)
- локальная формула Лапласа;
б)
- интегральная формула Лапласа, где Ф(z)- интегральная функция Лапласа
Слайд 8Основные законы распределения дискретных случайных величин
При тех же условиях, но когда
При этом:
Слайд 9Непрерывная случайная величина. Способы ее задания
Непрерывной случайной величиной называется случайная величина,
Интегральная функция распределения непрерывной случайной величины:
Дифференциальная функция распределения непрерывной случайной величины (функция плотности распределения):
Слайд 11Числовые характеристики непрерывной дискретной случайной величины
Математическое ожидание:
Дисперсия:
где
Среднее квадратичное отклонение:
Вероятность попадания в промежуток:
Слайд 12Основные законы распределения непрерывных случайных величин
1. Равномерное распределение:
Дифференциальная функция
распределения -
Интегральная
распределения -
Слайд 13Основные законы распределения непрерывных случайных величин
2. Показательное (экспоненциальное) распределение непрерывной случайной
Дифференциальная функция
распределения –
Интегральная функция
распределения -
Слайд 14Основные законы распределения непрерывных случайных величин
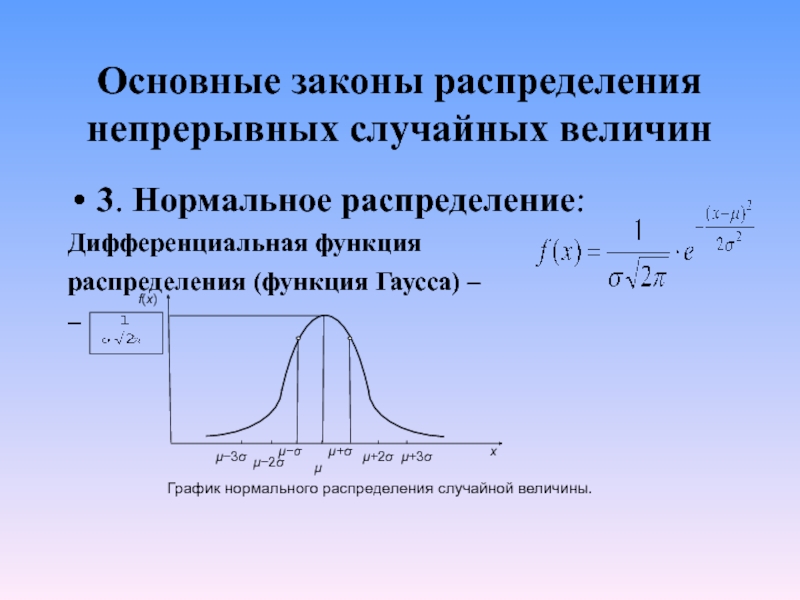
3. Нормальное распределение:
Дифференциальная функция
распределения (функция
–
Слайд 15Стандартная функция Лапласа
Если в функции Гаусса взять
Слайд 16Основные законы распределения непрерывных случайных величин
3. Нормальное распределение
Вероятность попадания нормально распределенной
где - интегральная функция Лапласа, ее значения находятся по таблице.
Правило трех сигм: если случайная величина нормально распределена, то практически достоверно, то есть с вероятностью, близкой к единице, ее значения лежат на промежутке [μ−3σ; μ+3σ].