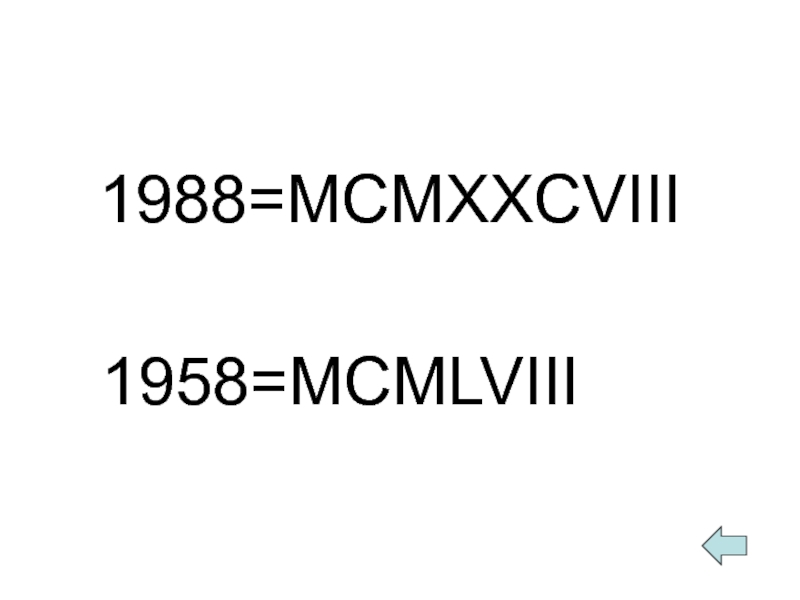- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления презентация
Содержание
- 1. Системы счисления
- 2. Система счисления – это способ записи чисел с помощью специальных знаков (цифр).
- 3. {0, 1, 2, …, 9} – 10
- 4. Пример 1: 56 –
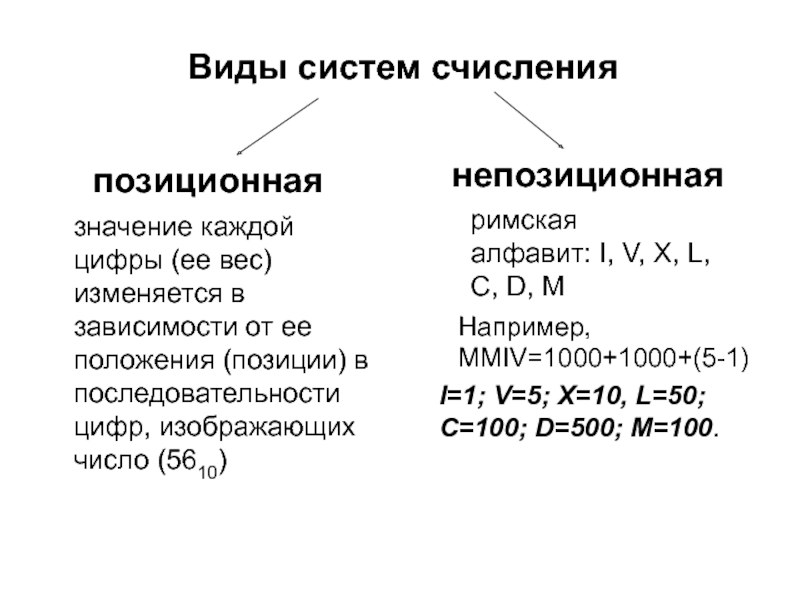
- 5. Виды систем счисления позиционная непозиционная значение каждой
- 6. 1988=MCMXXCVIII 1958=MCMLVIII
- 7. Существует ли какая-либо другая позиционная система счисления,
- 8. Будем рассматривать позиционные системы счисления (с.с.)
- 9. В старину на Руси широко применялась система
- 10. А какая система счисления лучше? Какие системы
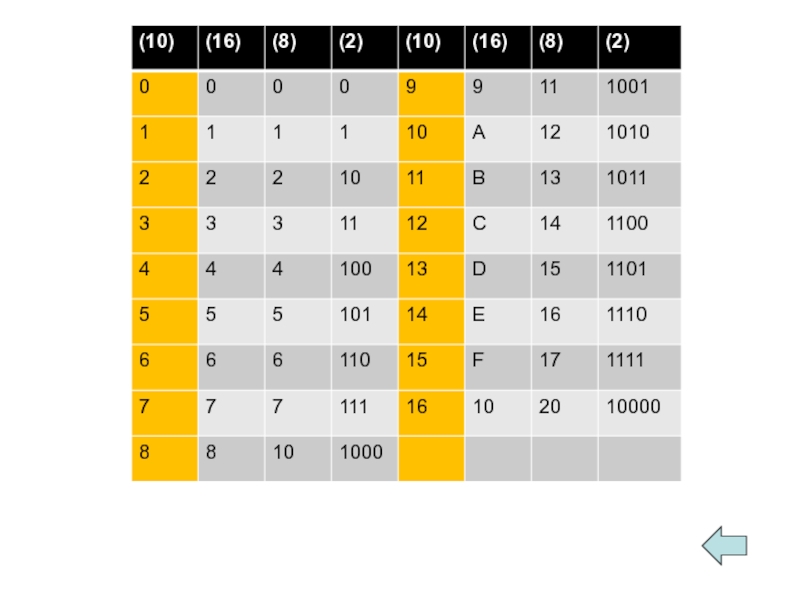
- 11. - двоичная (используются цифры
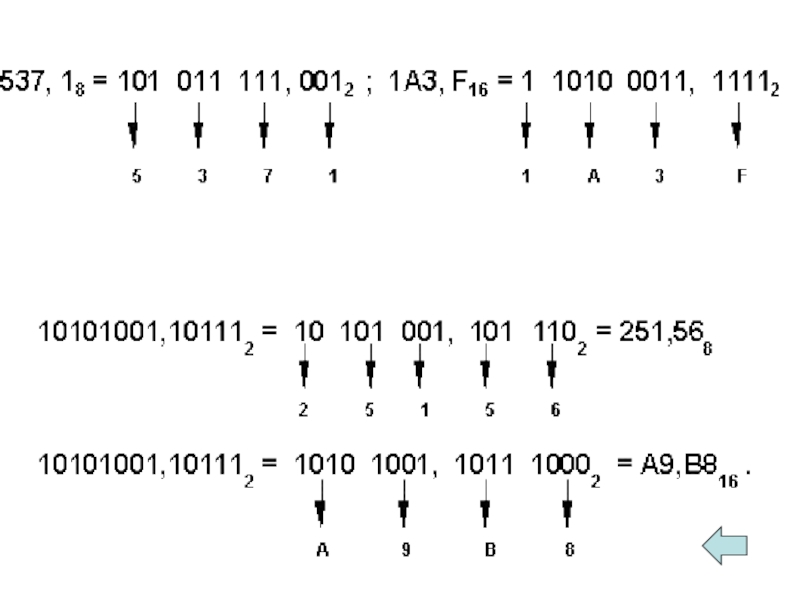
- 14. Цифры числа записывались, начиная с больших значений
- 15. Как перевести целое число из десятичной системы
- 16. Задачи Перевести числа 11, 89, 75 из
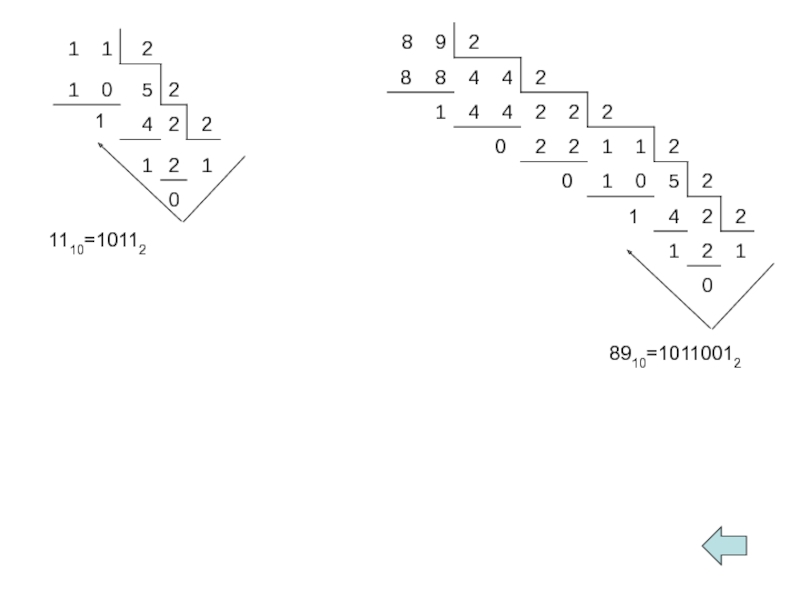
- 17. 1110=10112
- 18. 1110=10112 8910=10110012
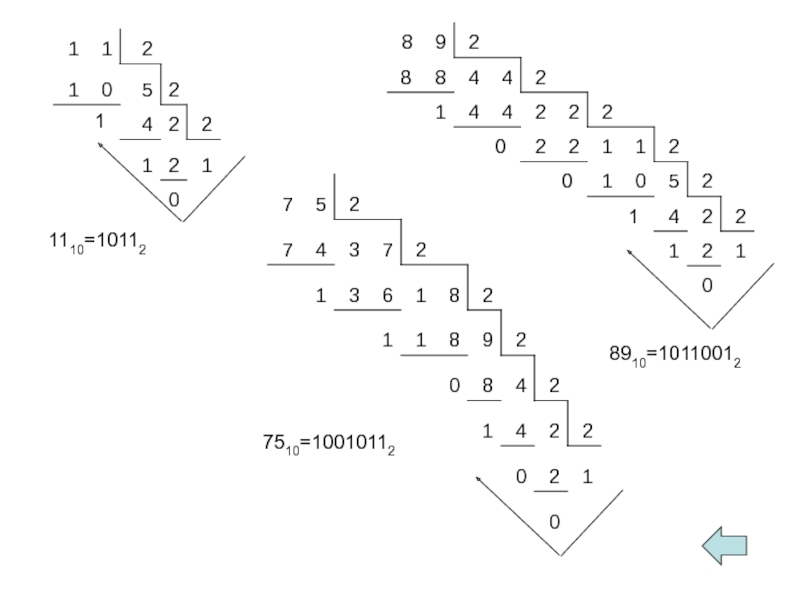
- 19. 1110=10112 7510=10010112 8910=10110012
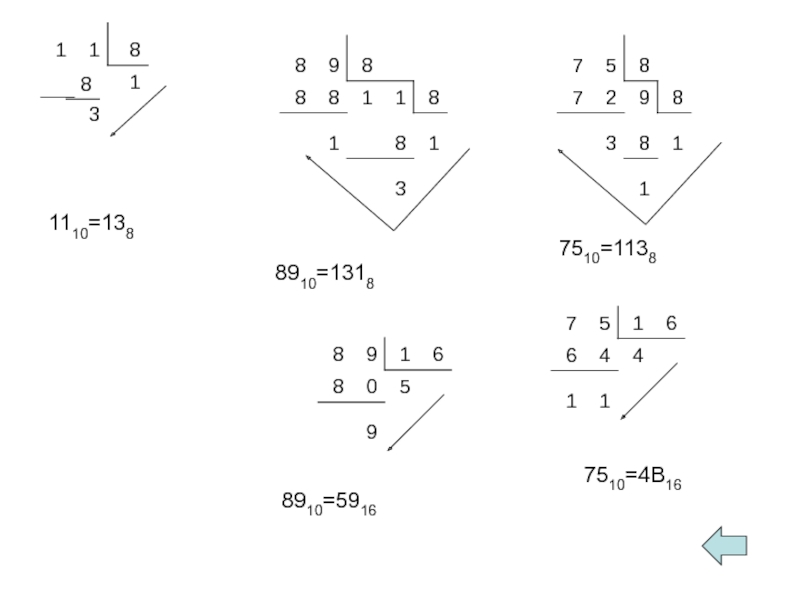
- 20. 1110=138 8910=1318 7510=1138 8910=5916 7510=4В16
- 21. Арифметические операции в позиционных системах счисления Рассмотрим
- 22. Таблицы сложения легко составить, используя Правило Счета.
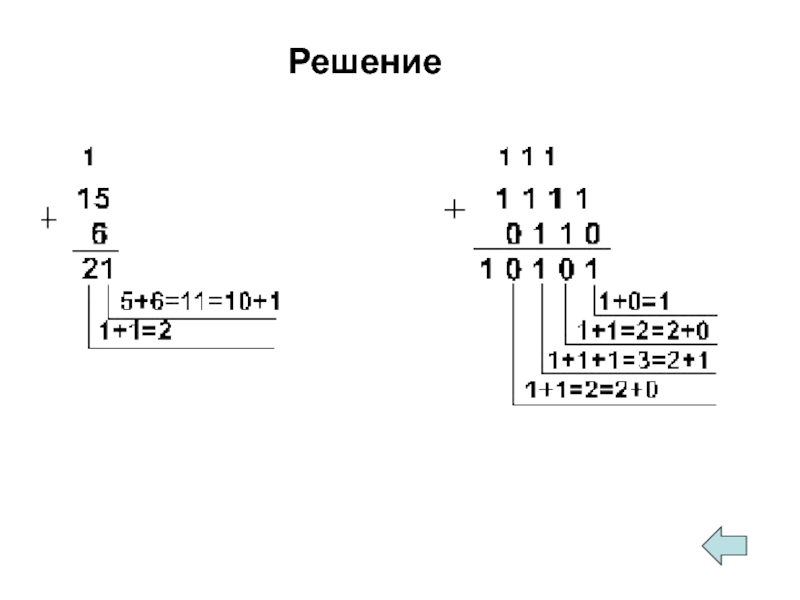
- 23. Решение
- 24. Сложение в восьмеричной системе счисления Задание. Сложить
- 25. Решение
- 26. Умножение Выполняя умножение многозначных чисел в различных
- 27. Умножение в двоичной и восьмеричной системах счисления
- 28. Решение Ответ: 5*6 = 3010 = 111102
- 29. Итоги 1. Определение системы счисления. 2.
- 30. Итоги 6. Системы счисления используемые специалистами
- 31. Домашнее задание § 45 1. Перевести числа
Слайд 3{0, 1, 2, …, 9} – 10 цифр (десятичная система счисления)
{0,
шестнацатеричная система счисл.
Основание с.с.( q ) это число цифр
используемых для записи числа.
В информатике используют с.с.
с основанием k=2,8,10,16
Слайд 4Пример 1: 56 –
65 -
5 десятков, 6 единиц,
6 десятков, 5 единиц.
Пример 2: Разложение числа 35748
35748=3*10000+5*1000+7*100+4*10+8=
=3*104+5*103+7*102+4*101+8*100
Слайд 5Виды систем счисления
позиционная
непозиционная
значение каждой цифры (ее вес) изменяется в зависимости от
римская
алфавит: I, V, X, L, C, D, M
I=1; V=5; X=10, L=50; C=100; D=500; M=100.
Например, MMIV=1000+1000+(5-1)
Слайд 7Существует ли какая-либо другая позиционная система счисления, отличная от десятичной?
Троичная. Ее
Пятиричная. Ее алфавит:
Одиннадцатиричная:
или 0, 1, 2, …, 9,
или 0, 1, 2, …, 9,
Примеры:
0, 1, 2, …, 9, А
0, 1, 2
0, 1, 2, 3, 4
Слайд 8Будем рассматривать позиционные системы
счисления (с.с.) в которых вес цифры зависит
ее позиции в числе.
Место q-ичной запятой
Слайд 9В старину на Руси широко применялась система счисления отдаленно напоминающая римскую.
- тысяча рублей, - десять рублей,
- сто рублей, X – один рубль,
IIIIIIIIII – десять копеек, I – одна копейка.
Слайд 10А какая система счисления лучше?
Какие системы счисления используют специалисты для общения
Почему люди пользуются десятичной системой, а компьютеры – двоичной?
Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
Слайд 11- двоичная (используются цифры )
0, 1
0, 1,
(для первых целых чисел от 0 до 9 используются цифры 0, 1, …, 9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F)
- восьмеричная (используются цифры )
- шестнадцатеричная
Слайд 14Цифры числа записывались, начиная с больших значений и заканчивая меньшими, слева
Слайд 15Как перевести целое число из десятичной системы в любую другую позиционную
Число в системе с основанием q записывается как последо-вательность остатков от деления, записанных в обратном порядке, начиная с последнего.
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q–1.
7510 = 1 001 0112 = 1138
Слайд 16Задачи
Перевести числа 11, 89, 75 из десятичной системы счисления в двоичную,
Слайд 21Арифметические операции в позиционных системах счисления
Рассмотрим основные арифметические операции: сложение, умножение.
Слайд 22Таблицы сложения легко составить, используя Правило Счета.
Сложение
Задание. Сложить в двоичной системе
Сложение в двоичной системе счисления
Решение.
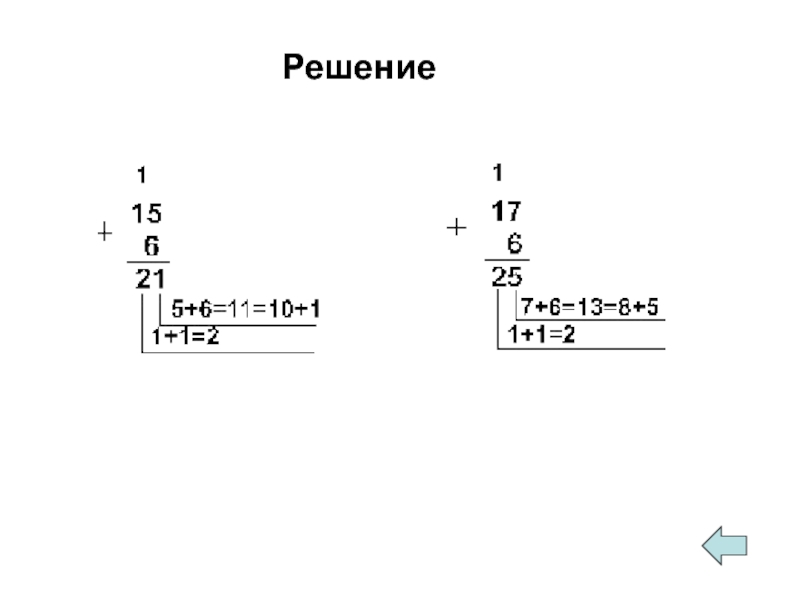
Слайд 24Сложение в восьмеричной системе счисления
Задание. Сложить в восьмеричной системе счисления числа:
Решение.
Слайд 26Умножение
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать
Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.
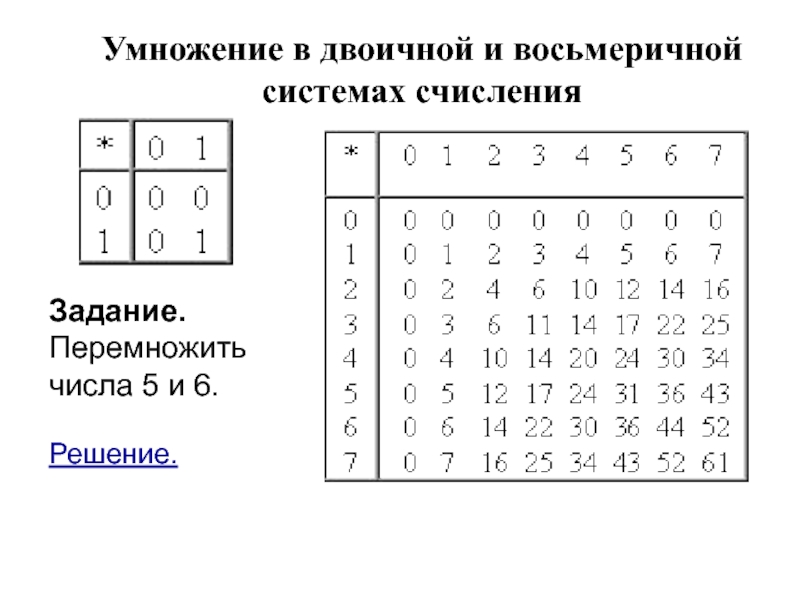
Слайд 27Умножение в двоичной и восьмеричной системах счисления
Задание. Перемножить числа 5
Решение.
Слайд 28Решение
Ответ: 5*6 = 3010 = 111102 = 368.
Проверка. Преобразуем полученные
Слайд 29Итоги
1. Определение системы счисления.
2. Виды систем счисления.
3. Удобство позиционной системы
4. Алфавит и основание позиционной системы счисления.
5. Разложение чисел в позиционной системе счисления.
Слайд 30Итоги
6. Системы счисления используемые специалистами для общения с компьютером.
7. Причины
8. История систем счисления.
9. Правило перевода целого числа из десятичной системы в любую другую позиционную систему счисления.
Слайд 31Домашнее задание
§ 45
1. Перевести числа 11, 89, 75 из десятичной системы
2. Сложить и умножить двоичные числа:
11102 и 1012 (проверить правильность своих действий).