- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы линейных уравнений с двумя переменными. Основные понятия презентация
Содержание
- 1. Системы линейных уравнений с двумя переменными. Основные понятия
- 2. Что называют системой уравнений? Системой уравнений называется
- 3. Решить систему уравнений - значит найти все
- 4. Алгоритм решения системы уравнений графическим способом 1.
- 5. Графический метод решения системы
- 6. y=0,5x-1 Y=0,5x+2 x x y y 0
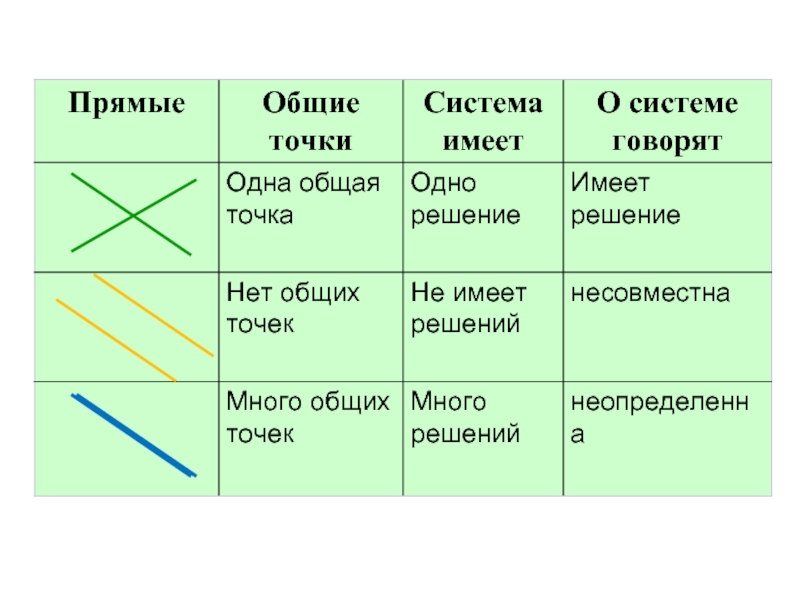
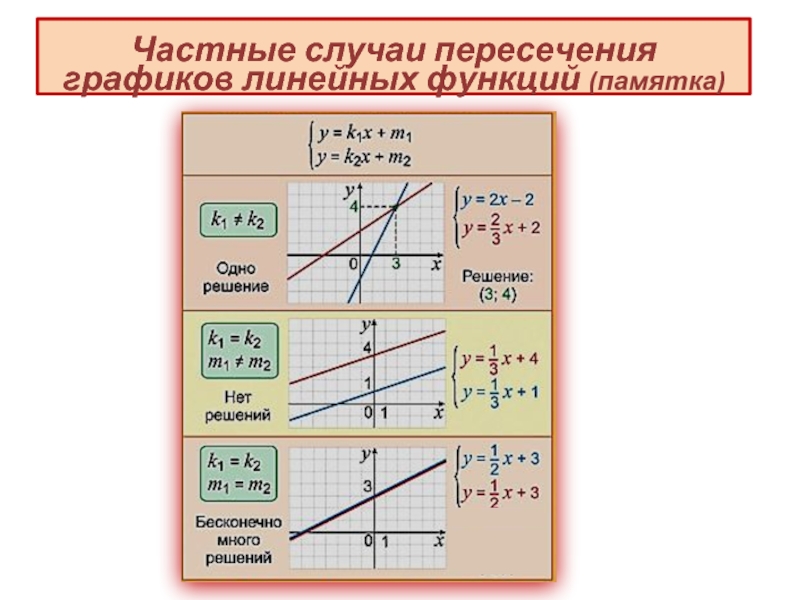
- 9. Частные случаи пересечения графиков линейных функций (памятка)
- 10. Системы линейных уравнений с двумя переменными. Метод подстановки.
- 11. Достоинство графического способа –наглядность. Недостаток графического способа–приближённые значения переменных. Плюсы и минусы графического метода
- 12. Решим систему уравнений 3x -
- 13. Алгоритм решения системы уравнений методом подстановки 1.
- 14. Домашнее задание Параграфы 12 и 13. № 12.3 № 12.4
Слайд 2Что называют системой уравнений?
Системой уравнений называется некоторое количество уравнений, объединенных фигурной
Где а1, b1, c1, a2, b2, c2 – заданные числа. х и у - переменные
Слайд 3Решить систему уравнений - значит найти все её решения или установить,
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство.
Каждая пара значений переменных, которая одновременно является решением всех уравнений системы, называется решением системы.
Слайд 4Алгоритм решения системы уравнений графическим способом
1. Приводим оба уравнения к виду
2. Составляем расчётные таблицы для каждой функции.
3. Строим графики функций в одной координатной плоскости.
4. Определяем число решений:
Если прямые пересекаются, то одно решение пара чисел (х ; у) – координаты точки пересечения;
Если прямые параллельны, то нет решений;
Если прямые совпадают, то бесконечно много решений.
5. Записываем ответ.
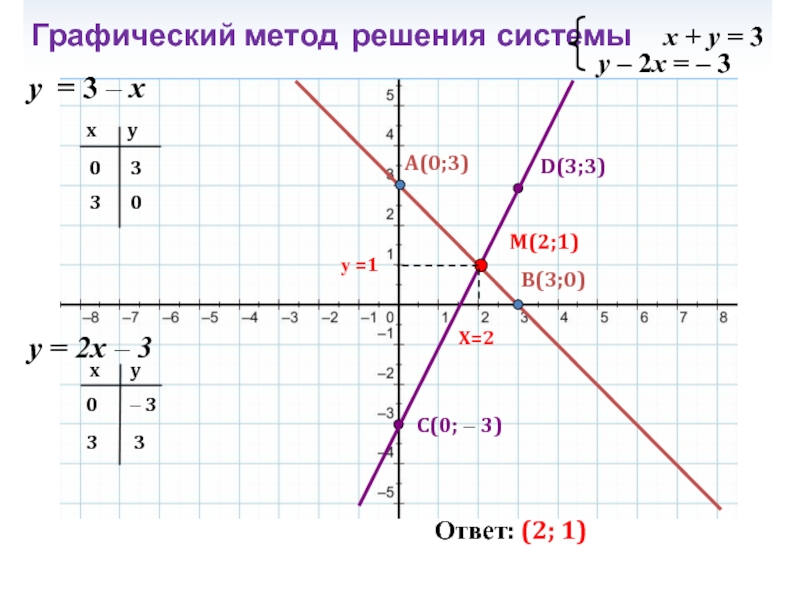
Слайд 5Графический метод решения системы x + y =
у = 3 – x
у = 2x – 3
x
y
0
3
x
y
0
3
3
0
– 3
3
A(0;3)
B(3;0)
C(0; – 3)
D(3;3)
M(2;1)
X=2
у =1
Ответ: (2; 1)
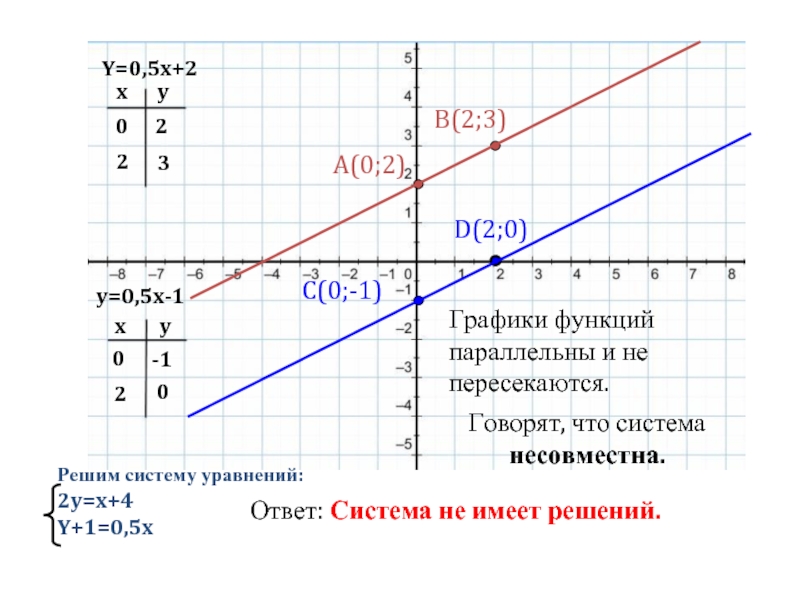
Слайд 6y=0,5x-1
Y=0,5x+2
x
x
y
y
0
2
2
3
0
-1
2
0
A(0;2)
B(2;3)
C(0;-1)
D(2;0)
Решим систему уравнений: 2y=x+4
Графики функций параллельны и не пересекаются.
Говорят, что система несовместна.
Ответ: Система не имеет решений.
Слайд 7
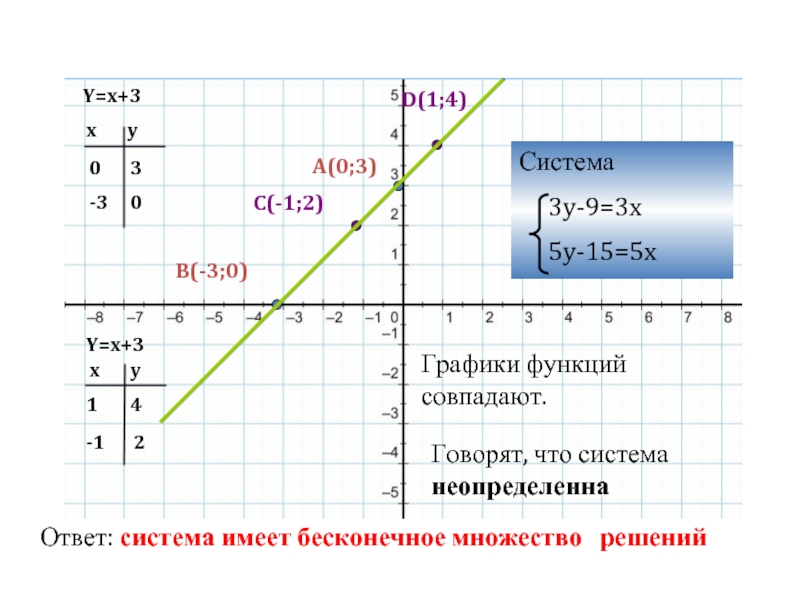
Y=x+3
Y=x+3
x
y
0
-3
x
y
1
-1
3
0
4
2
A(0;3)
B(-3;0)
C(-1;2)
D(1;4)
Система
3y-9=3x
5y-15=5x
Графики функций совпадают.
Говорят, что система неопределенна
Ответ: система имеет бесконечное множество решений
Слайд 11Достоинство графического способа –наглядность.
Недостаток графического способа–приближённые значения переменных.
Плюсы и минусы графического
Слайд 12Решим систему уравнений
3x - y - 5 = 0
1) Из первого уравнения получаем: у = 3х - 5
2) Подставим найденное выражение вместо у во второе уравнение системы: 2х + (3х - 5) - 7 = 0
3) Решим полученное уравнение:
2х + 3х - 5 - 7 = 0
5х - 12 = 0
5х = 12
х = 2,4
4) Подставим найденное значение х в формулу у = 3х - 5
у = 3 2,4 - 5 = 7,2 - 5 = 2,2
5) Пара х = 2,4 ; у = 2,2 - единственное решение заданной системы.
Слайд 13Алгоритм решения системы уравнений методом подстановки
1. Выразить у через х из
2. Подставить полученное на первом шаге выражение вместо у во второе уравнение системы.
3. Решить полученное на втором шаге уравнение относительно х.
4. Подставить найденное на третьем шаге значение х в выражение у через х, полученное на первом шаге.
5. Записываем ответ в виде пары значений (х;у), которые мы нашли на предыдущих шагах.