- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы линейных алгебраических уравнений презентация
Содержание
- 1. Системы линейных алгебраических уравнений
- 2. Система m линейных алгебраических уравнений c n
- 3. Опр. Решить систему означает найти все совокупности
- 4. Опр: Матрица составленная из коэффициентов системы называется
- 5. Метод Крамера
- 6. По формулам Крамера решаются только неоднородные системы.
- 7. Опр: Определитель Δ основной матрицы называется главным
- 8. Опр: Дополнительным определителем называется определитель полученный из
- 9. Теорема: Если определитель системы Δ не равен
- 10. Теорема: Если определитель системы Δ=0, и хотя
- 11. Теорема:Если определитель системы ∆=0, и ∆1=∆2=∆3=0, то система имеет бесконечное множество решений. (неопределенная система).
- 12. Матричный метод решения СЛАУ
- 13. Системе 3х линейных уравнений соответствует матричное уравнение
- 14. Метод не работает, если число уравнений не
Слайд 2Система m линейных алгебраических уравнений c n неизвестными имеет вид:
а11х1
+ а12х2 + .....+ а1nхn = в1
а21х1 + а22х2 + ….+ а2nхn = в2
………………………………
аm1х1 + аm2х2 + ….+ аmnхn = вm
аij – коэффициенты, хj - неизвестные, bi - свободные члены уравнений.
а21х1 + а22х2 + ….+ а2nхn = в2
………………………………
аm1х1 + аm2х2 + ….+ аmnхn = вm
аij – коэффициенты, хj - неизвестные, bi - свободные члены уравнений.
Слайд 3Опр. Решить систему означает найти все совокупности значений неизвестных (х1, х2,....хn),
удовлетворяющих системе или показать, что система не имеет решений.
1.Если система не имеет решений, то она называется несовместимой.
2. Если она имеет единственное решение – определенной.
3. Если она имеет бесконечно много решений – неопределенной.
Опр: Если хотя бы одно из чисел bi, отлично от нуля, система называется неоднородной. Если все свободные члены равны нулю, то система называется однородной.
1.Если система не имеет решений, то она называется несовместимой.
2. Если она имеет единственное решение – определенной.
3. Если она имеет бесконечно много решений – неопределенной.
Опр: Если хотя бы одно из чисел bi, отлично от нуля, система называется неоднородной. Если все свободные члены равны нулю, то система называется однородной.
Слайд 4Опр: Матрица составленная из коэффициентов системы называется основной матрицей, если к
основной матрице приписать справа столбец свободных членов, то получится расширенная матрица системы.
Слайд 8Опр: Дополнительным определителем называется определитель полученный из главного определителя путем замены
j-го столбца столбцом свободных членов.
Δ1=
Δ1=
Δ2=
Δ3=
.
Слайд 9Теорема: Если определитель системы Δ не равен 0, то система имеет
единственное решение, которое находится по формулам:
Х1 = Δ1/ Δ;
х2== Δ2/ Δ;
х3== Δ3/ Δ
Х1 = Δ1/ Δ;
х2== Δ2/ Δ;
х3== Δ3/ Δ
Слайд 10Теорема: Если определитель системы Δ=0, и хотя бы один из определителей
∆1, ∆2, ∆3 отличен от нуля, то система несовместна(т.е. не имеет решений).
Слайд 11Теорема:Если определитель системы ∆=0, и ∆1=∆2=∆3=0, то система имеет бесконечное множество
решений. (неопределенная система).
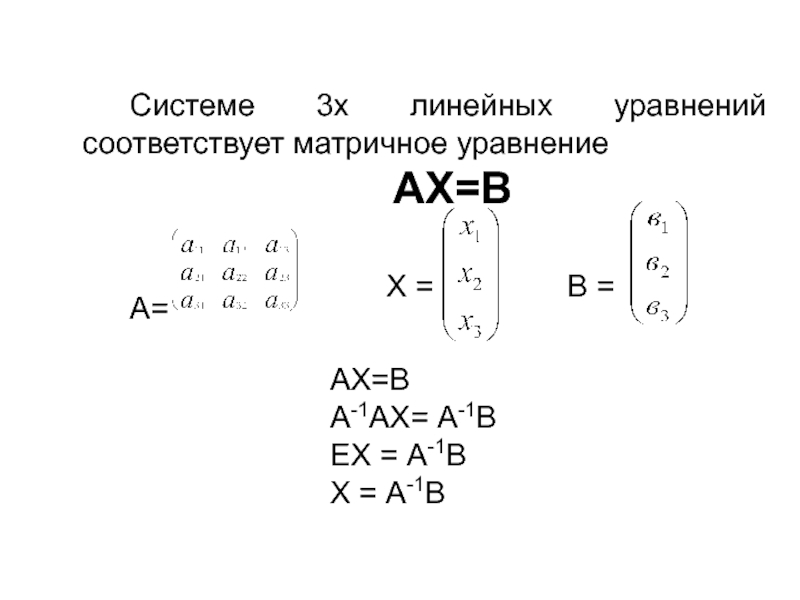
Слайд 13Системе 3х линейных уравнений соответствует матричное уравнение
АХ=В
А=
Х =
В
=
АХ=В
А-1АХ= А-1В
ЕХ = А-1В
Х = А-1В
Слайд 14Метод не работает, если число уравнений не равно числу неизвестных, или
когда матрица системы хотя и квадратна, но вырождена (тогда не существует обратной матрицы, т.е определитель основной матрицы равен нулю).