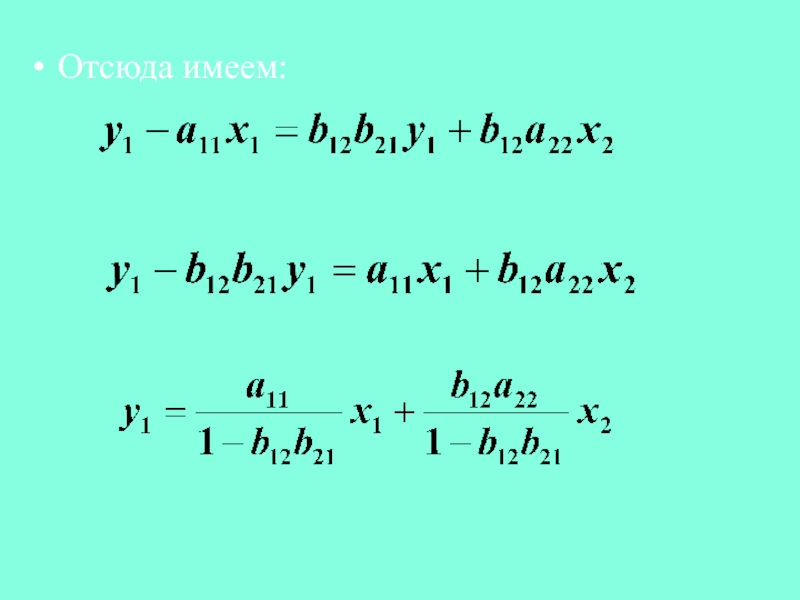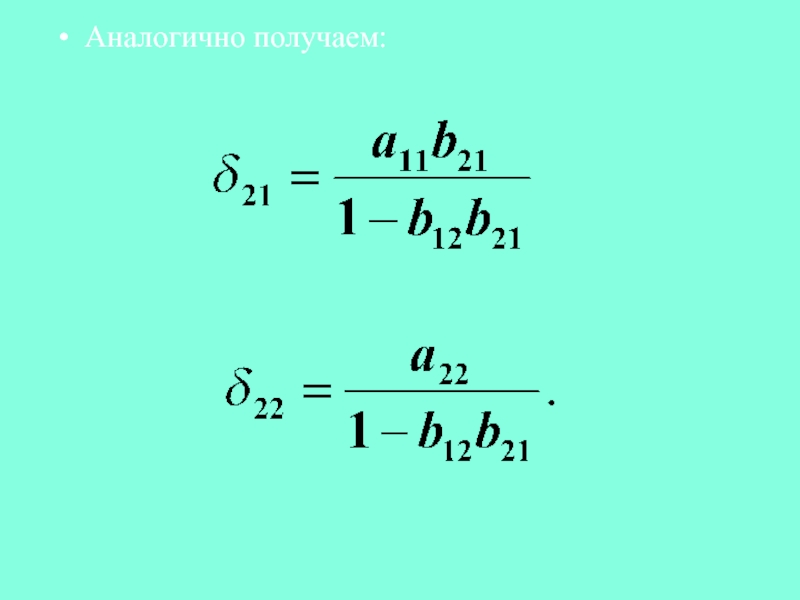А.С.
Студент 1 курса Магистерской
подготовки экономика.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы эконометрических уравнений презентация
Содержание
- 1. Системы эконометрических уравнений
- 2. 1. система независимых уравнений (когда каждая зависимая
- 3. Набор факторов в каждом уравнении может
- 4. Каждое уравнение системы независимых уравнений может рассматриваться
- 5. 2. системы рекурсивных уравнений:
- 6. Примером такой системы может служить модель производительности
- 7. 3. система взаимозависимых уравнений (системы совместных, одновременных уравнений ).
- 8. Пример: модель динамики цены и заработной платы
- 9. В отличие от предыдущих систем каждое уравнение
- 10. Система совместных, одновременных уравнений обычно содержит
- 11. структурные коэффициенты модели:
- 12. для определения структурных коэффициентов модели структурная форма
- 13. Пример: Для структурной модели вида
- 14. из первого уравнения получаем:
- 15. Отсюда имеем:
- 16. Таким образом, мы представили первое уравнение
- 17. Аналогично получаем:
- 18. Проблема идентификации. Идентификация - единственность соответствия между приведенной и структурной формами модели.
- 19. С позиции идентифицируемости структурные модели можно подразделить
- 20. Модель идентифицируема, если все структурные ее коэффициенты
- 21. Модель неидентифицируема, если число приведенных коэффициентов меньше
- 22. Модель сверхидентифицируема, если число приведенных коэффициентов
- 23. обозначим H -число эндогенных переменных в
- 24. Модель считается идентифицируемой, если каждое уравнение системы
- 25. СПАСИБО ЗА ВНИМАНИЕ
1. система независимых уравнений (когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x)
Слайд 21. система независимых уравнений (когда каждая зависимая переменная y рассматривается как
функция одного и того же набора факторов x)
Слайд 3 Набор факторов в каждом уравнении может варьироваться. Так, модель вида
также
является системой независимых уравнений.
Слайд 4Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его
параметров используется метод наименьших квадратов.
Слайд 5 2. системы рекурсивных уравнений:
зависимая переменная включает в каждое
последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов x.
Слайд 6Примером такой системы может служить модель производительности труда и фондоотдачи вида:
где
- производительность труда;
- фондоотдача;
- фондовооруженность труда;
-энерговооруженность труда;
- квалификация рабочих.
- фондоотдача;
- фондовооруженность труда;
-энерговооруженность труда;
- квалификация рабочих.
Слайд 8Пример: модель динамики цены и заработной платы вида
-
темп изменения месячной заработной платы;
- темп изменения цен;
- процент безработных;
- темп изменения постоянного капитала;
- темп изменения цен на импорт сырья.
- темп изменения цен;
- процент безработных;
- темп изменения постоянного капитала;
- темп изменения цен на импорт сырья.
Слайд 9В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не
может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим.
Слайд 10 Система совместных, одновременных уравнений обычно содержит эндогенные и экзогенные переменные.
Эндогенные переменные (y). Это зависимые переменные, число которых равно числу уравнений в системе.
Экзогенные переменные (x). Это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них.
Слайд 11
структурные коэффициенты модели:
- коэффициент при эндогенной
переменной,
- коэффициент при экзогенной переменной
- коэффициент при экзогенной переменной
Слайд 12для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную
форму модели.
Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:
-коэффициенты приведенной формы модели.
Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:
-коэффициенты приведенной формы модели.
Слайд 16 Таким образом, мы представили первое уравнение структурной формы модели в
виде уравнения приведенной формы модели:
Отсюда
Отсюда
Слайд 18Проблема идентификации.
Идентификация - единственность соответствия между приведенной и структурной формами модели.
Слайд 19С позиции идентифицируемости структурные модели можно подразделить на три вида:
идентифицируемые;
неидентифицируемые;
сверхидентифицируемые.
неидентифицируемые;
сверхидентифицируемые.
Слайд 20Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом
по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели.
Слайд 21Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и
в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
Слайд 22
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В
этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента.
Слайд 23обозначим
H -число эндогенных переменных в j – м уравнении системы,
D - число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение,
то условие идентифицируемости модели может быть записано в виде:
—уравнение идентифицируемо;
— уравнение неидентифицируемо;
— уравнение сверхидентифицируемо.
Слайд 24Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо.
Если хотя бы
одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой.
Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
