- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия в жизни презентация
Содержание
- 1. Симметрия в жизни
- 2. Симметрия Греческое слово «симметрия» означает «соразмерность», «пропорциональность»,
- 3. Виды симметрии Зеркальная (Осевая)
- 4. Зеркальная(Осевая) Зеркальная симметрия связывает любой предмет и
- 6. Центральная Точка A' называется симметричной точке А
- 7. Центральная симметрия в природе
- 8. Симметрия вращения Ось симметрии n-го порядка -
- 9. Симметрия вращения
- 10. Бордюр Бордюр - совокупность равных фигур, повторяющихся
- 11. Бордюр
- 12. Спасибо за внимание
Слайд 2Симметрия
Греческое слово «симметрия» означает «соразмерность», «пропорциональность», «одинаковость в расположении частей». Однако
часто под словом «симметрия» понимают более широкое понятие: регулярность смены каких-либо явлений (времен года, дня и ночи и т.д.), уравновешенность левого и правого, равноправие природных явлений. Фактически мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность.
Слайд 4Зеркальная(Осевая)
Зеркальная симметрия связывает любой предмет и его отражение в плоском зеркале.
Говорят, что одна фигура зеркально симметрично другой, если вместе они образуют зеркально симметричную фигуру Симметрично зеркальные фигуры при всём своём сходстве существенно отличаются друг от друга. Две зеркально симметричные плоские фигуры всегда можно наложить друг на друга. Однако для этого необходимо вывести одну из них из их общей плоскости.
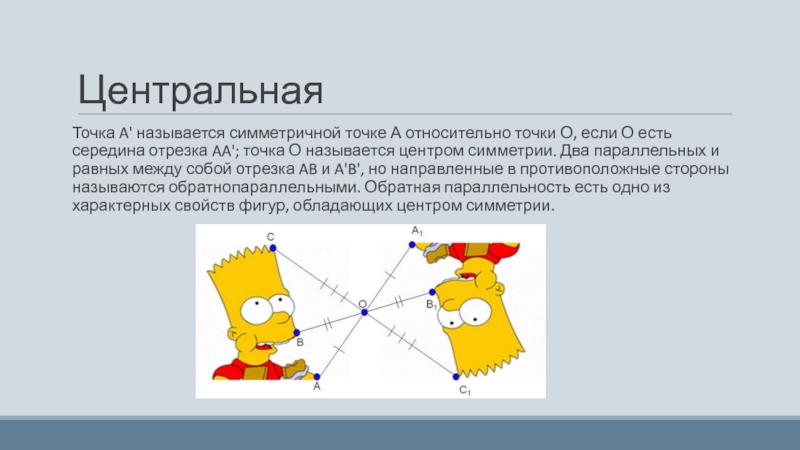
Слайд 6Центральная
Точка A' называется симметричной точке А относительно точки О, если О
есть середина отрезка AA'; точка О называется центром симметрии. Два параллельных и равных между собой отрезка AB и A'B', но направленные в противоположные стороны называются обратнопараллельными. Обратная параллельность есть одно из характерных свойств фигур, обладающих центром симметрии.
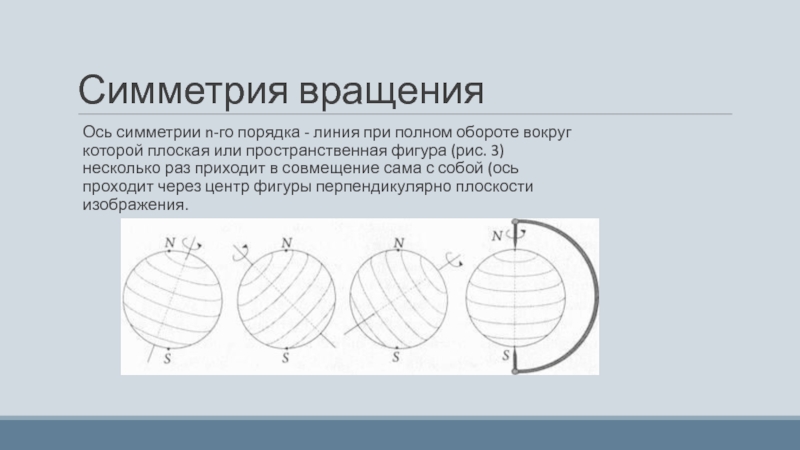
Слайд 8Симметрия вращения
Ось симметрии n-го порядка - линия при полном обороте вокруг
которой плоская или пространственная фигура (рис. 3) несколько раз приходит в совмещение сама с собой (ось проходит через центр фигуры перпендикулярно плоскости изображения.
Слайд 10Бордюр
Бордюр - совокупность равных фигур, повторяющихся последовательно одна за другой вдоль
прямой линии - оси переноса. Общее число всех возможных видов симметрии бордюров – семь.