- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия в пространстве презентация
Содержание
- 1. Симметрия в пространстве
- 2. Понятие преобразования для фигур в пространстве определяется
- 3. Симметрия относительно точки Точки М
- 4. Симметрия относительно прямой Точки А
- 5. Симметрия относительно плоскости Это преобразование
- 6. Зеркальная симметрия (преобладает в животном и растительном мире)
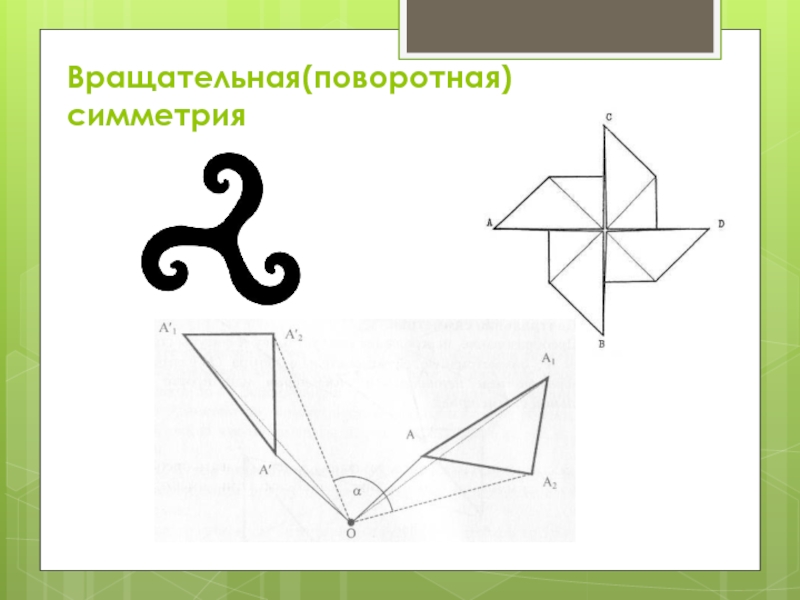
- 7. Вращательная(поворотная) симметрия
- 8. Скользящая симметрия
Слайд 2Понятие преобразования для фигур в пространстве определяется так же, как и
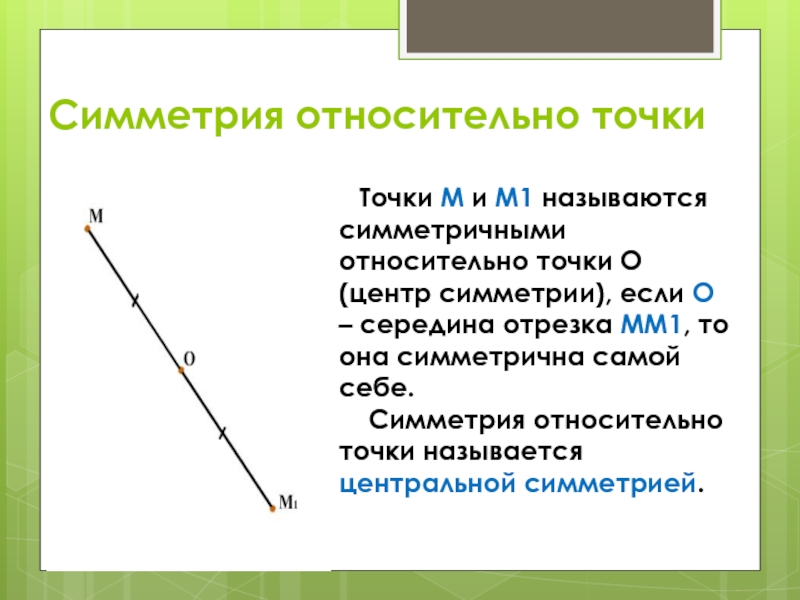
Слайд 3Симметрия относительно точки
Точки М и М1 называются симметричными относительно
Симметрия относительно точки называется центральной симметрией.
Слайд 4Симметрия относительно прямой
Точки А и А1 называются симметричными относительно
Симметрия относительно прямой называется осевой симметрией.
Слайд 5Симметрия
относительно
плоскости
Это преобразование состоит в следующем. Пусть — произвольная
Если точка X лежит в плоскости α, то считается, что точка X переходит в себя. Если преобразование симметрии относительно плоскости α переводит фигуру в себя, то фигура называется симметричной относительно плоскости α, а плоскость α называется плоскостью симметрии этой фигуры.