его оснований и боковой поверхности (касается каждой образующей). При этом цилиндр называется описанным около сферы.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сфера, вписанная в цилиндр презентация
Содержание
- 1. Сфера, вписанная в цилиндр
- 2. Сфера, вписанная в цилиндр В цилиндр можно
- 3. Упражнение 1 В цилиндр высоты 2 вписана сфера. Найдите ее радиус. Ответ: 1.
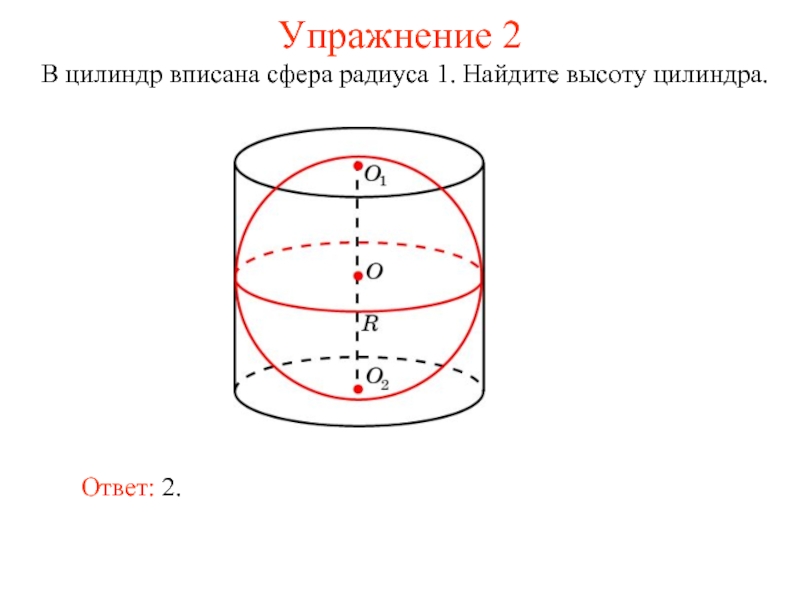
- 4. Упражнение 2 В цилиндр вписана сфера радиуса 1. Найдите высоту цилиндра. Ответ: 2.
- 5. Упражнение 3 Радиус основания цилиндра равен 2.
- 6. Упражнение 4 Высота цилиндра равна 2. Каким
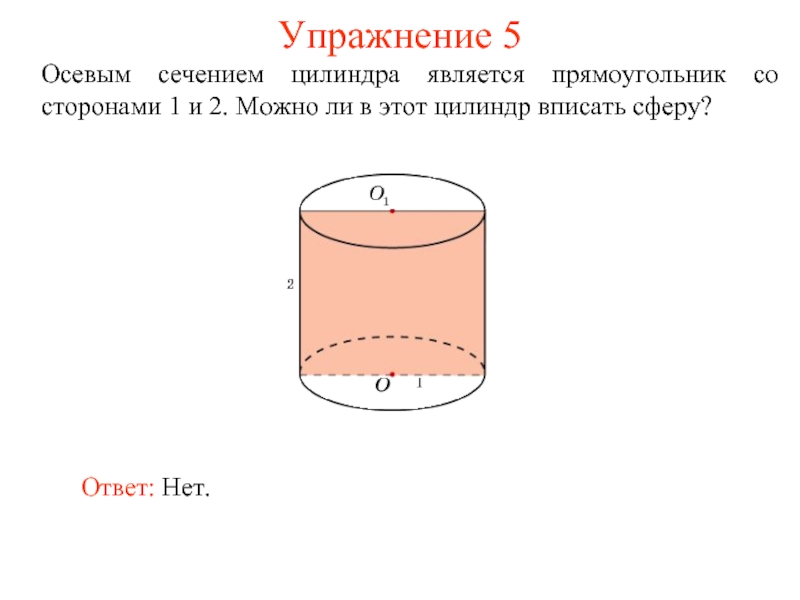
- 7. Упражнение 5 Осевым сечением цилиндра является прямоугольник
- 8. Упражнение 6 Осевым сечением цилиндра является квадрат.
- 9. Упражнение 7 Можно ли вписать сферу в цилиндр, осевым сечением которого является ромб? Ответ: Нет.
- 10. Упражнение 8 Можно ли вписать сферу в наклонный цилиндр? Ответ: Нет.
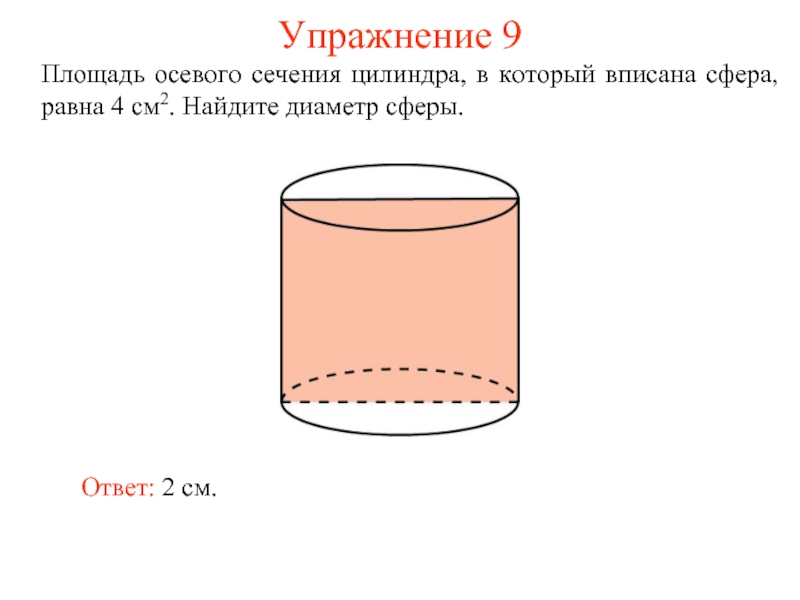
- 11. Упражнение 9 Площадь осевого сечения цилиндра, в
- 12. Упражнение 10 Периметр осевого сечения цилиндра, в
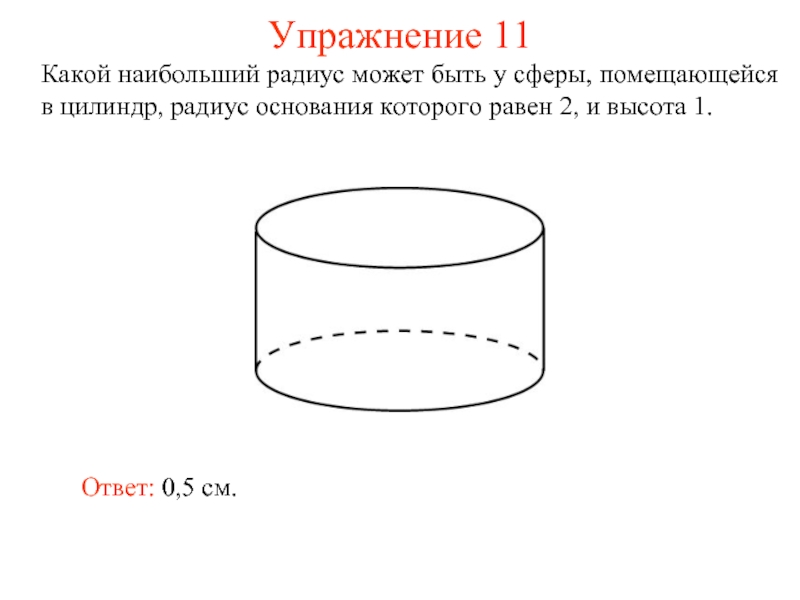
- 13. Упражнение 11 Какой наибольший радиус может быть
- 14. Упражнение 12 Можно ли сферу радиуса 1
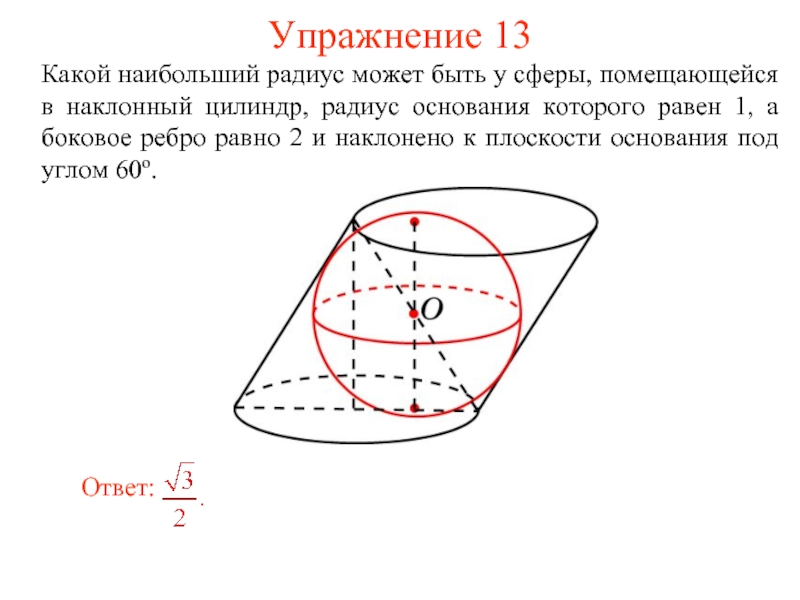
- 15. Упражнение 13 Какой наибольший радиус может быть
- 16. Упражнение 14 На рисунке изображена ортогональная проекция сферы. Нарисуйте цилиндр описанный около этой сферы.
- 17. Упражнение 15 На рисунке изображена ортогональная проекция
- 18. Сфера, описанная около цилиндра Цилиндр называется вписанным
- 19. Сфера, описанная около цилиндра
- 20. Упражнение 1 Диагональ осевого сечения цилиндра равна
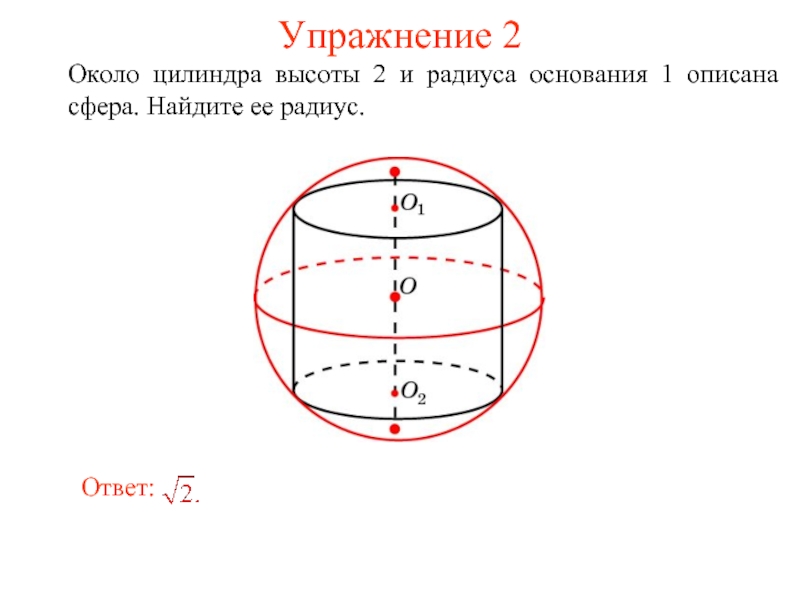
- 21. Упражнение 2 Около цилиндра высоты 2 и радиуса основания 1 описана сфера. Найдите ее радиус.
- 22. Упражнение 3 Около цилиндра, радиус основания которого
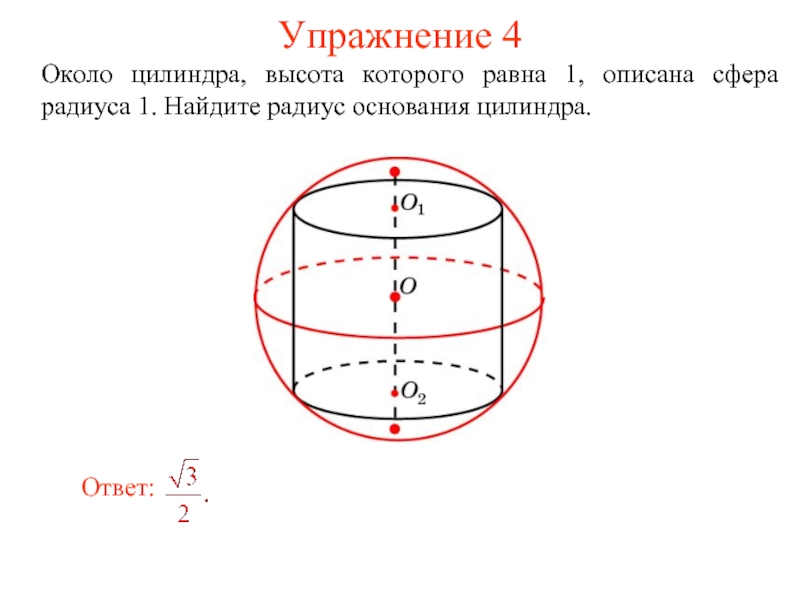
- 23. Упражнение 4 Около цилиндра, высота которого равна
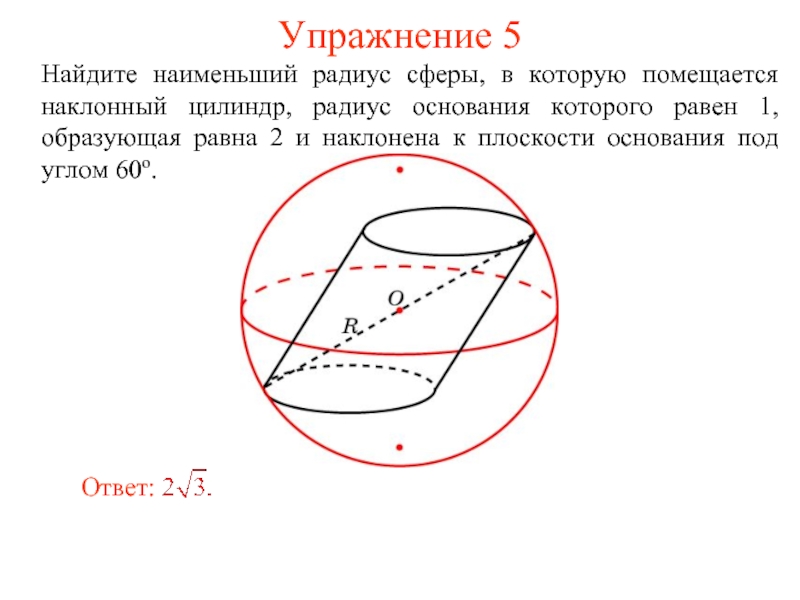
- 24. Упражнение 5 Найдите наименьший радиус сферы, в
- 25. Цилиндр, вписанный в призму Цилиндр называется вписанным
- 26. Цилиндр, вписанный в призму В призму можно
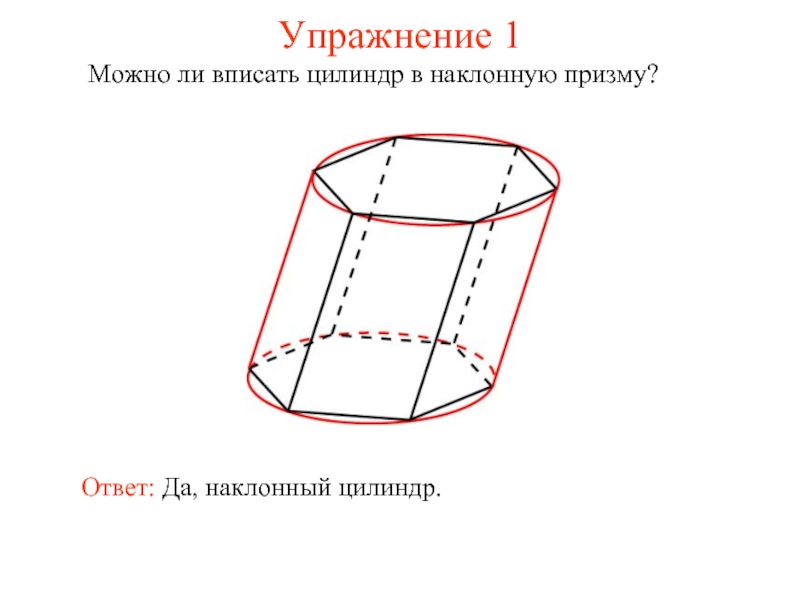
- 27. Упражнение 1 Можно ли вписать цилиндр в наклонную призму? Ответ: Да, наклонный цилиндр.
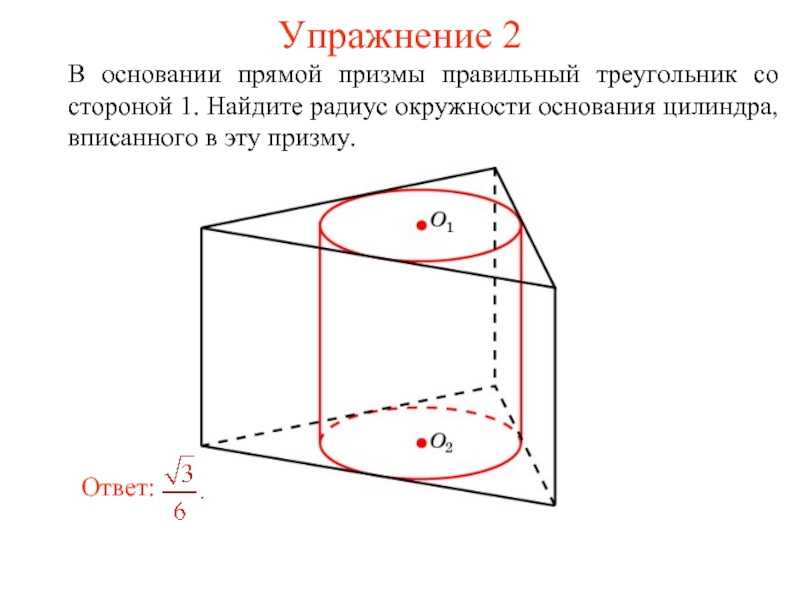
- 28. Упражнение 2 В основании прямой призмы правильный
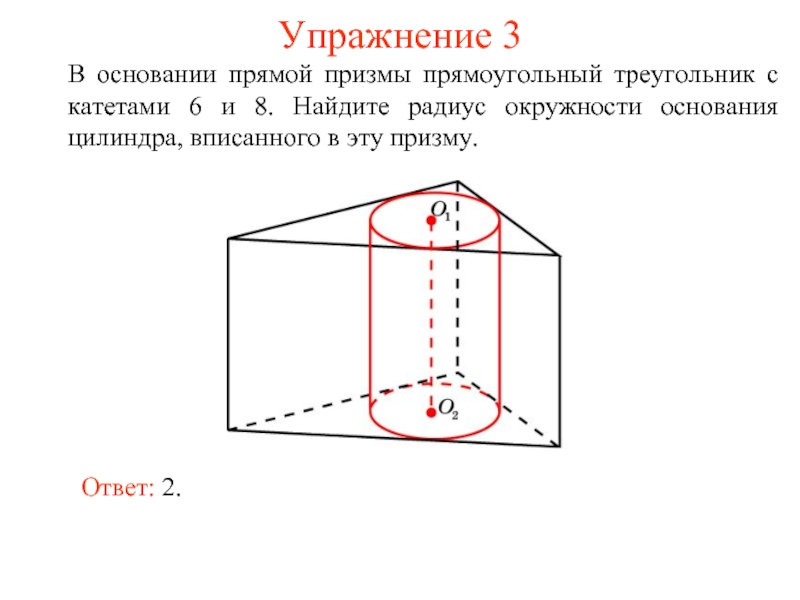
- 29. Упражнение 3 В основании прямой призмы прямоугольный
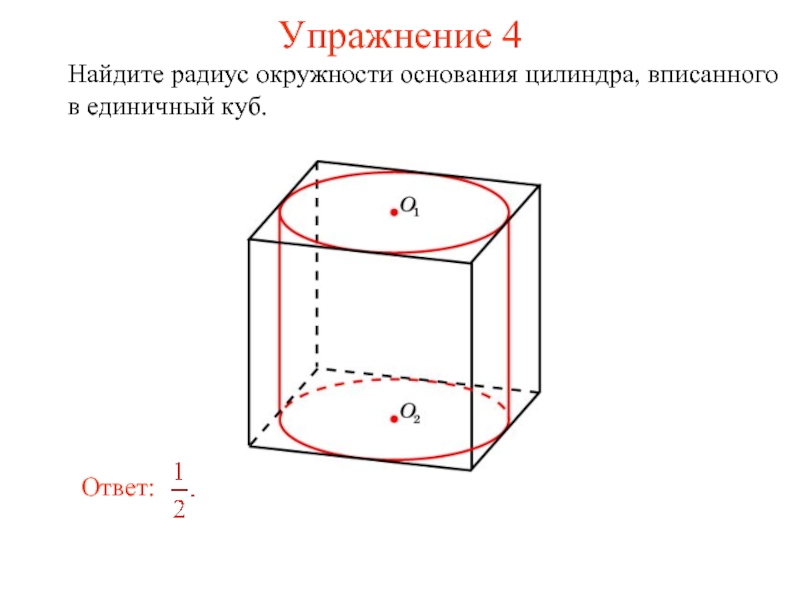
- 30. Упражнение 4 Найдите радиус окружности основания цилиндра, вписанного в единичный куб.
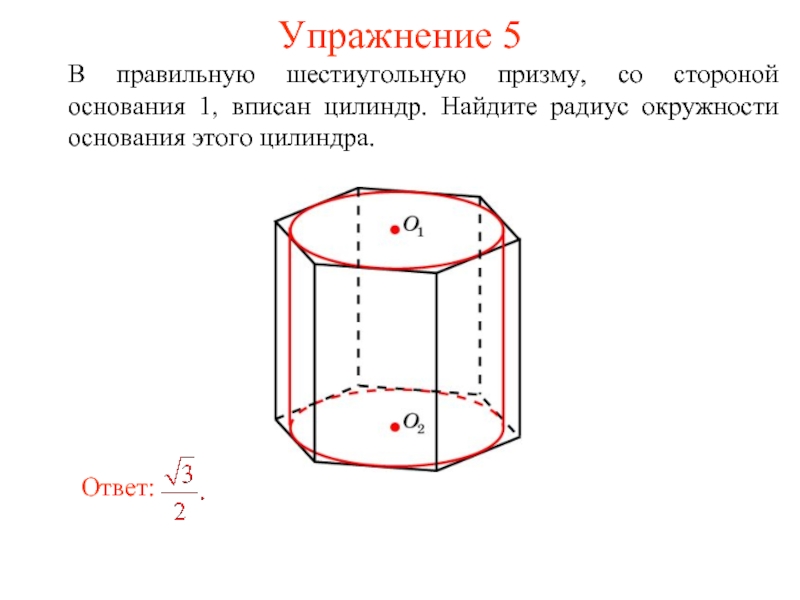
- 31. Упражнение 5 В правильную шестиугольную призму, со
- 32. Упражнение 6 На рисунке изображена ортогональная проекция
- 33. Упражнение 7 На рисунке изображена ортогональная проекция
- 34. Упражнение 8 На рисунке изображена ортогональная проекция
- 35. Цилиндр, описанный около призмы Цилиндр называется описанным
- 36. Цилиндр, описанный около призмы Около призмы можно
- 37. Упражнение 1 Можно ли описать цилиндр около наклонной призмы? Ответ: Да, наклонный цилиндр.
- 38. Упражнение 2 В основании прямой призмы правильный
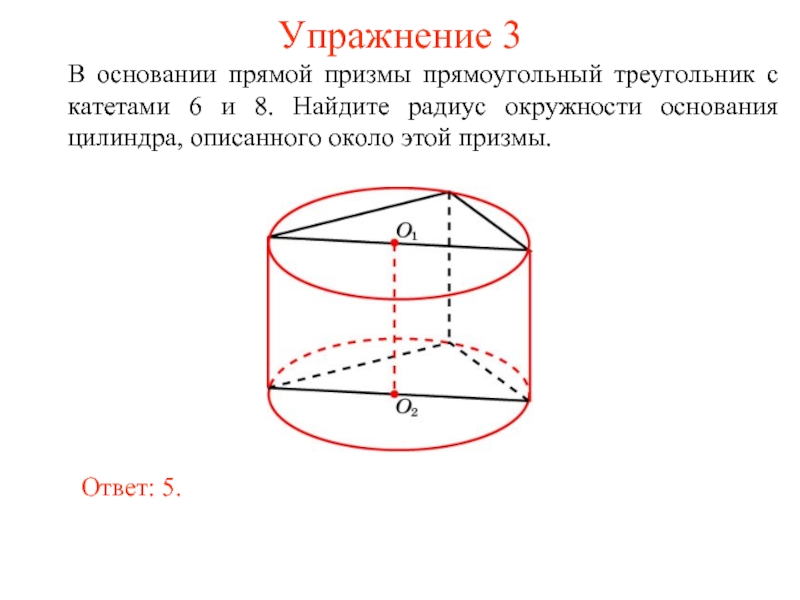
- 39. Упражнение 3 В основании прямой призмы прямоугольный
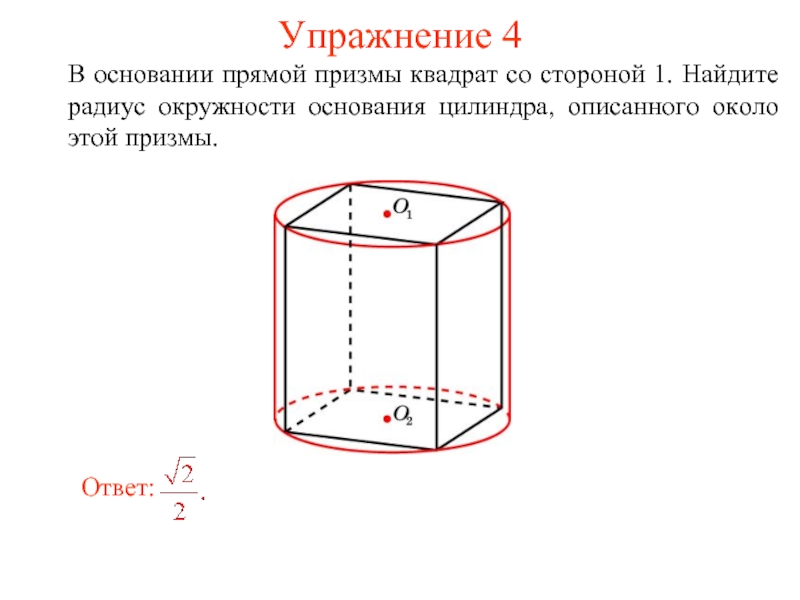
- 40. Упражнение 4 В основании прямой призмы квадрат
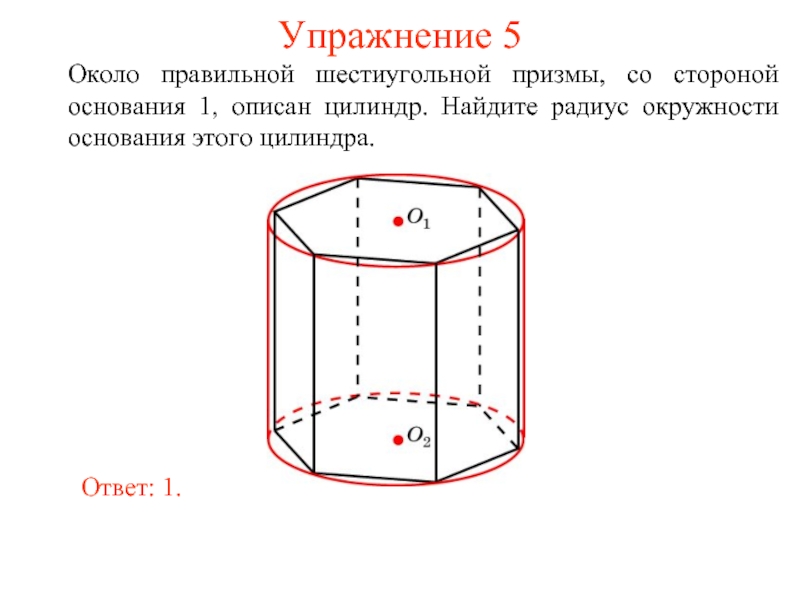
- 41. Упражнение 5 Около правильной шестиугольной призмы, со
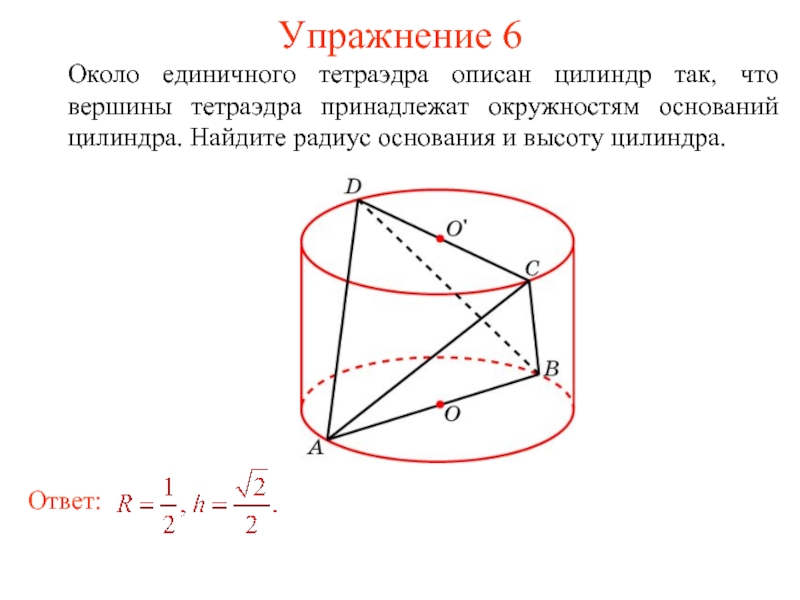
- 42. Упражнение 6 Около единичного тетраэдра описан цилиндр
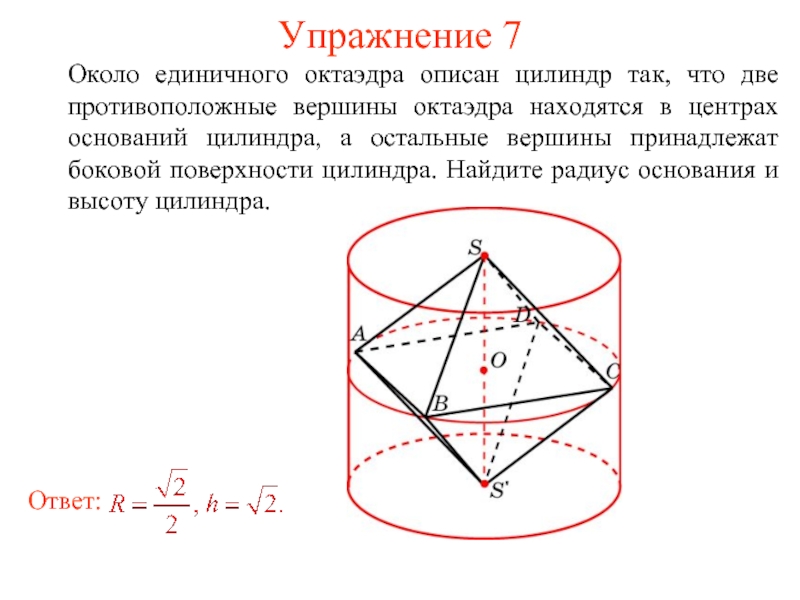
- 43. Упражнение 7 Около единичного октаэдра описан цилиндр
Сфера, вписанная в цилиндр В цилиндр можно вписать сферу, если высота цилиндра равна диаметру его основания. Ее центром будет точка O, являющаяся серединой отрезка, соединяющего центры оснований O1 и O2 цилиндра.
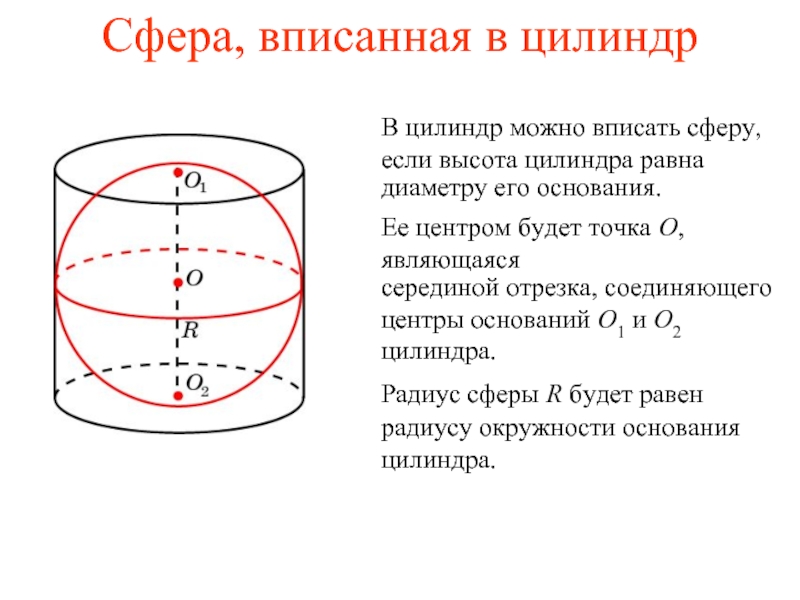
Слайд 2Сфера, вписанная в цилиндр
В цилиндр можно вписать сферу, если высота цилиндра
равна
диаметру его основания.
Ее центром будет точка O, являющаяся
серединой отрезка, соединяющего центры оснований O1 и O2 цилиндра.
Радиус сферы R будет равен
радиусу окружности основания цилиндра.
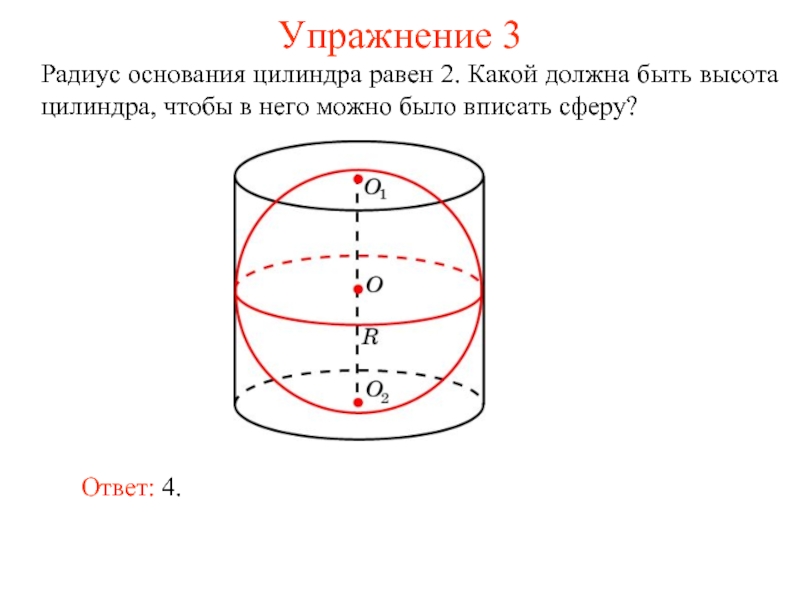
Слайд 5Упражнение 3
Радиус основания цилиндра равен 2. Какой должна быть высота цилиндра,
чтобы в него можно было вписать сферу?
Ответ: 4.
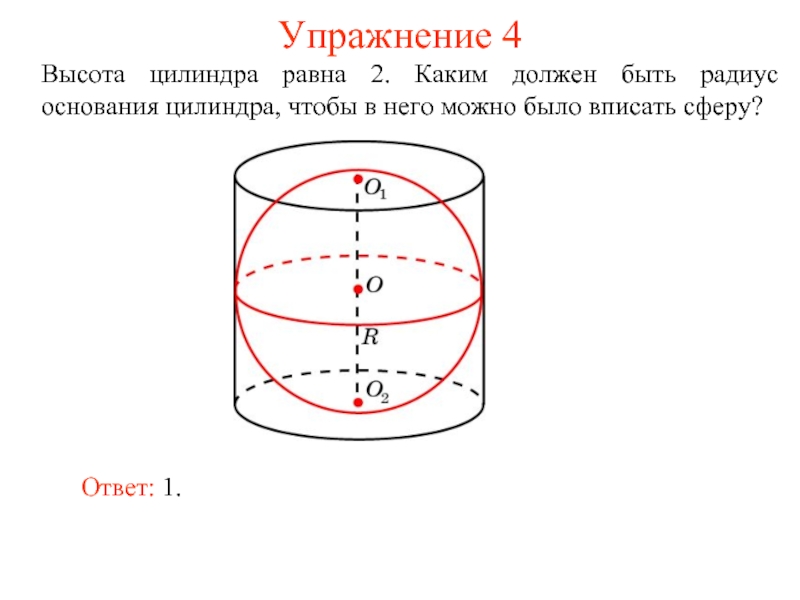
Слайд 6Упражнение 4
Высота цилиндра равна 2. Каким должен быть радиус основания цилиндра,
чтобы в него можно было вписать сферу?
Ответ: 1.
Слайд 7Упражнение 5
Осевым сечением цилиндра является прямоугольник со сторонами 1 и 2.
Можно ли в этот цилиндр вписать сферу?
Ответ: Нет.
Слайд 8Упражнение 6
Осевым сечением цилиндра является квадрат. Можно ли в этот цилиндр
вписать сферу?
Ответ: Да.
Слайд 9Упражнение 7
Можно ли вписать сферу в цилиндр, осевым сечением которого является
ромб?
Ответ: Нет.
Слайд 11Упражнение 9
Площадь осевого сечения цилиндра, в который вписана сфера, равна 4
см2. Найдите диаметр сферы.
Ответ: 2 см.
Слайд 12Упражнение 10
Периметр осевого сечения цилиндра, в который вписана сфера, равен 8
см. Найдите радиус сферы.
Ответ: 1 см.
Слайд 13Упражнение 11
Какой наибольший радиус может быть у сферы, помещающейся в цилиндр,
радиус основания которого равен 2, и высота 1.
Ответ: 0,5 см.
Слайд 14Упражнение 12
Можно ли сферу радиуса 1 поместить в наклонный цилиндр, радиус
основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.
Ответ: Нет.
Слайд 15Упражнение 13
Какой наибольший радиус может быть у сферы, помещающейся в наклонный
цилиндр, радиус основания которого равен 1, а боковое ребро равно 2 и наклонено к плоскости основания под углом 60о.
Слайд 16Упражнение 14
На рисунке изображена ортогональная проекция сферы. Нарисуйте цилиндр описанный около
этой сферы.
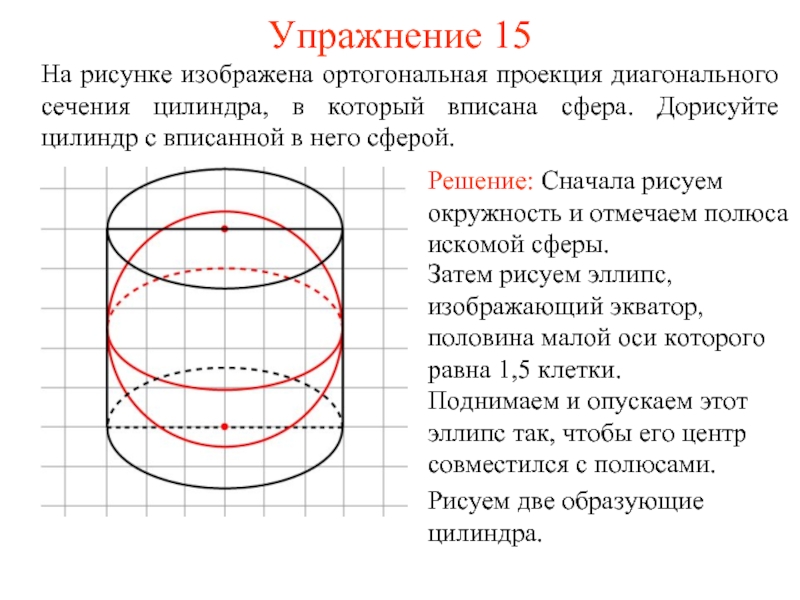
Слайд 17Упражнение 15
На рисунке изображена ортогональная проекция диагонального сечения цилиндра, в который
вписана сфера. Дорисуйте цилиндр с вписанной в него сферой.
Решение: Сначала рисуем окружность и отмечаем полюса искомой сферы.
Затем рисуем эллипс, изображающий экватор, половина малой оси которого равна 1,5 клетки.
Поднимаем и опускаем этот эллипс так, чтобы его центр совместился с полюсами.
Рисуем две образующие цилиндра.
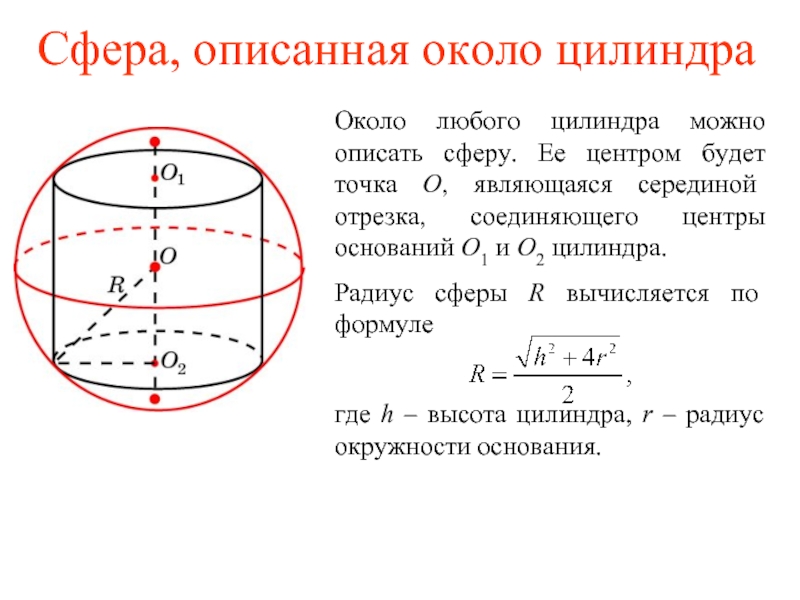
Слайд 18Сфера, описанная около цилиндра
Цилиндр называется вписанным в сферу, если окружности оснований
цилиндра лежат на сфере. При этом сфера называется описанной около цилиндра.
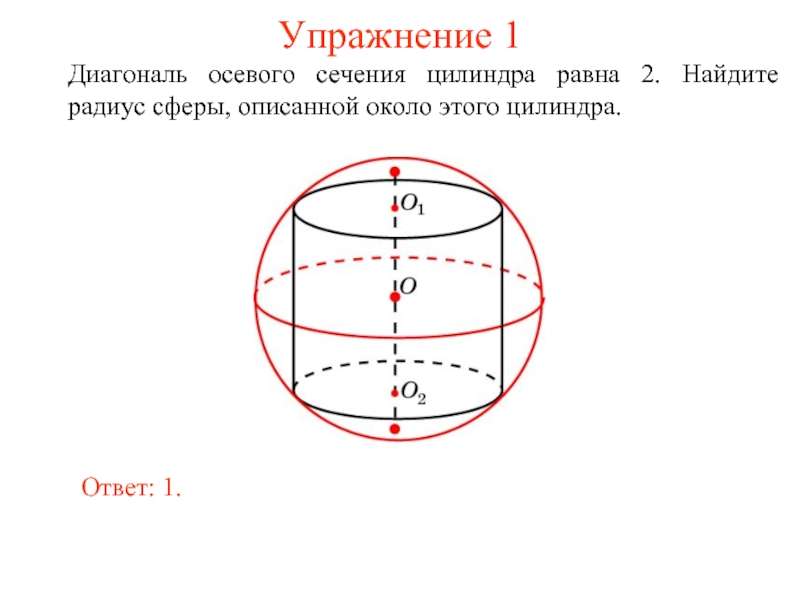
Слайд 20Упражнение 1
Диагональ осевого сечения цилиндра равна 2. Найдите радиус сферы, описанной
около этого цилиндра.
Ответ: 1.
Слайд 22Упражнение 3
Около цилиндра, радиус основания которого равен 1, описана сфера радиуса
2. Найдите высоту цилиндра.
Слайд 23Упражнение 4
Около цилиндра, высота которого равна 1, описана сфера радиуса 1.
Найдите радиус основания цилиндра.
Слайд 24Упражнение 5
Найдите наименьший радиус сферы, в которую помещается наклонный цилиндр, радиус
основания которого равен 1, образующая равна 2 и наклонена к плоскости основания под углом 60о.
Слайд 25Цилиндр, вписанный в призму
Цилиндр называется вписанным в призму, если его основания
вписаны в основания цилиндра. При этом, призма называется описанной около цилиндра
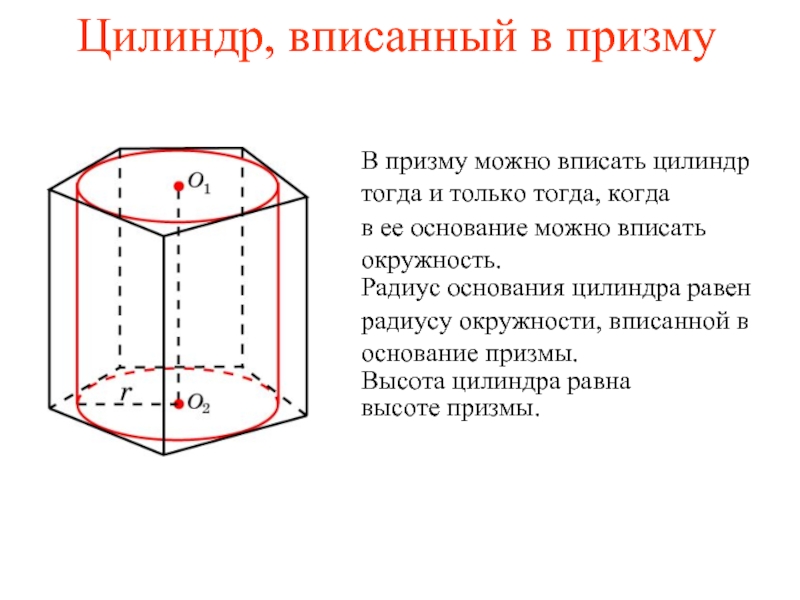
Слайд 26Цилиндр, вписанный в призму
В призму можно вписать цилиндр тогда и только
тогда, когда
в ее основание можно вписать окружность.
Радиус основания цилиндра равен
радиусу окружности, вписанной в основание призмы.
Высота цилиндра равна
высоте призмы.
Слайд 28Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите
радиус окружности основания цилиндра, вписанного в эту призму.
Слайд 29Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и
8. Найдите радиус окружности основания цилиндра, вписанного в эту призму.
Ответ: 2.
Слайд 31Упражнение 5
В правильную шестиугольную призму, со стороной основания 1, вписан цилиндр.
Найдите радиус окружности основания этого цилиндра.
Слайд 32Упражнение 6
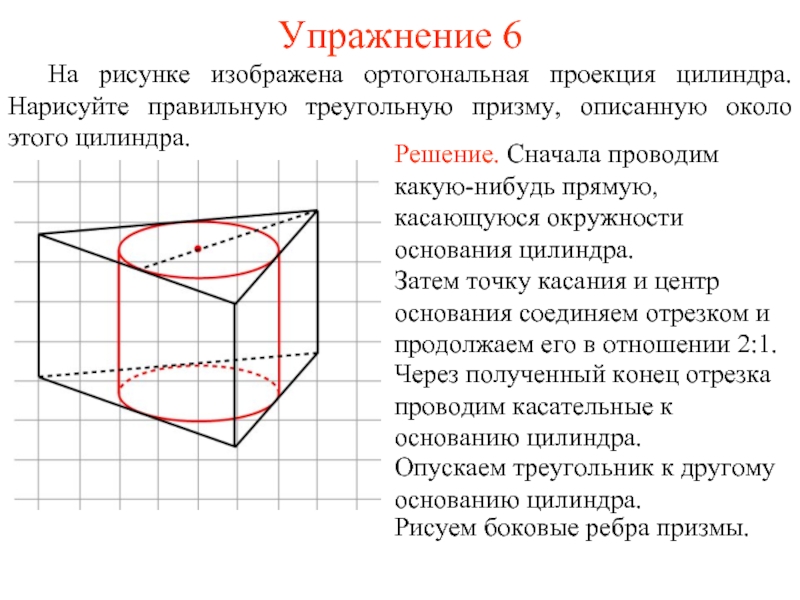
На рисунке изображена ортогональная проекция цилиндра. Нарисуйте правильную треугольную призму,
описанную около этого цилиндра.
Решение. Сначала проводим какую-нибудь прямую, касающуюся окружности основания цилиндра.
Затем точку касания и центр основания соединяем отрезком и продолжаем его в отношении 2:1.
Через полученный конец отрезка проводим касательные к основанию цилиндра.
Опускаем треугольник к другому основанию цилиндра.
Рисуем боковые ребра призмы.
Слайд 33Упражнение 7
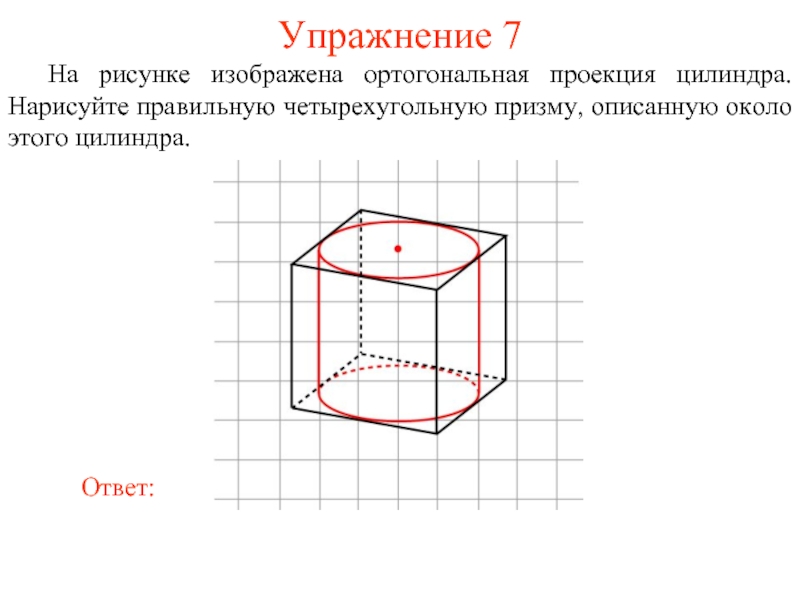
На рисунке изображена ортогональная проекция цилиндра. Нарисуйте правильную четырехугольную призму,
описанную около этого цилиндра.
Слайд 34Упражнение 8
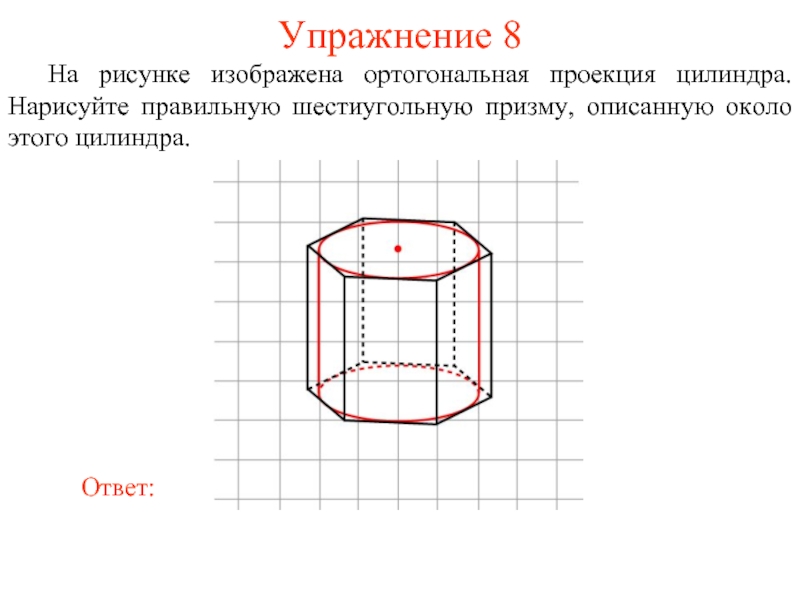
На рисунке изображена ортогональная проекция цилиндра. Нарисуйте правильную шестиугольную призму,
описанную около этого цилиндра.
Слайд 35Цилиндр, описанный около призмы
Цилиндр называется описанным около призмы, если его основания
описаны около оснований цилиндра. При этом, призма называется вписанной в цилиндр
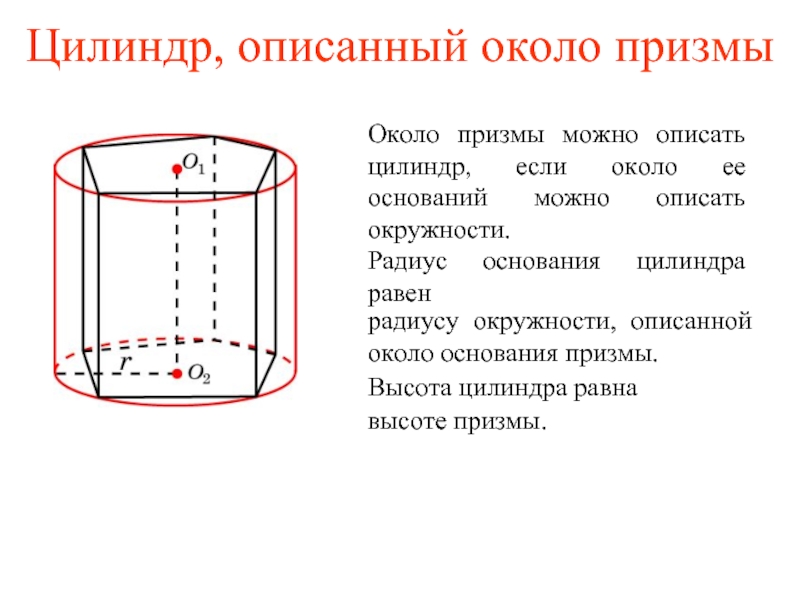
Слайд 36Цилиндр, описанный около призмы
Около призмы можно описать цилиндр, если около ее
оснований можно описать окружности.
Высота цилиндра равна
высоте призмы.
радиусу окружности, описанной около основания призмы.
Радиус основания цилиндра равен
Слайд 38Упражнение 2
В основании прямой призмы правильный треугольник со стороной 1. Найдите
радиус окружности основания цилиндра, описанного около этой призмы.
Слайд 39Упражнение 3
В основании прямой призмы прямоугольный треугольник с катетами 6 и
8. Найдите радиус окружности основания цилиндра, описанного около этой призмы.
Ответ: 5.
Слайд 40Упражнение 4
В основании прямой призмы квадрат со стороной 1. Найдите радиус
окружности основания цилиндра, описанного около этой призмы.
Слайд 41Упражнение 5
Около правильной шестиугольной призмы, со стороной основания 1, описан цилиндр.
Найдите радиус окружности основания этого цилиндра.
Ответ: 1.
Слайд 42Упражнение 6
Около единичного тетраэдра описан цилиндр так, что вершины тетраэдра принадлежат
окружностям оснований цилиндра. Найдите радиус основания и высоту цилиндра.
Слайд 43Упражнение 7
Около единичного октаэдра описан цилиндр так, что две противоположные вершины
октаэдра находятся в центрах оснований цилиндра, а остальные вершины принадлежат боковой поверхности цилиндра. Найдите радиус основания и высоту цилиндра.
