- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сечения многогранника (задачи) презентация
Содержание
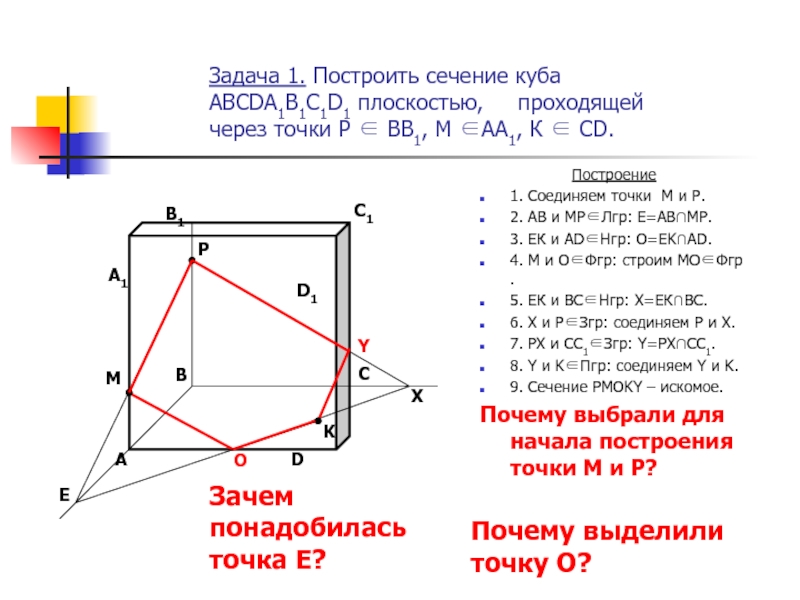
Слайд 2Задача 1. Построить сечение куба ABCDA1B1C1D1 плоскостью, проходящей через
Построение
1. Соединяем точки М и Р.
2. АВ и МР∈Лгр: Е=АВ∩МР.
3. ЕК и AD∈Нгр: O=EK∩AD.
4. М и О∈Фгр: строим МО∈Фгр .
5. ЕК и ВС∈Нгр: Х=ЕК∩ВС.
6. Х и Р∈Згр: соединяем Р и X.
7. PX и СС1∈Згр: Y=PX∩CC1.
8. Y и K∈Пгр: соединяем Y и K.
9. Сечение PMOKY – искомое.
Почему выбрали для начала построения точки М и Р?
Р
M
K
A1
B1
C1
D1
A
B
C
D
E
O
X
Y
Зачем понадобилась точка Е?
Почему выделили точку О?
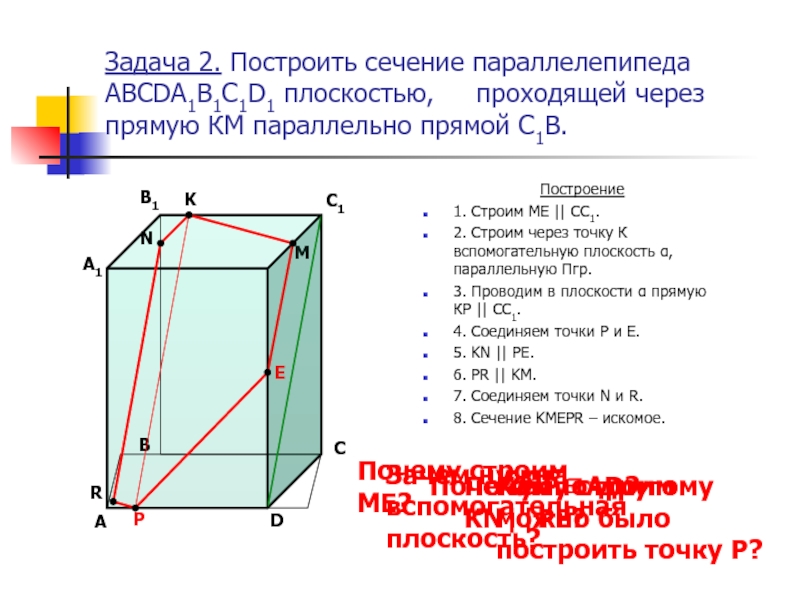
Слайд 3Задача 2. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через
Построение
1. Строим МЕ || CC1.
2. Строим через точку К вспомогательную плоскость α, параллельную Пгр.
3. Проводим в плоскости α прямую
КР || CC1.
4. Соединяем точки Р и Е.
5. KN || PE.
6. PR || KM.
7. Соединяем точки N и R.
8. Сечение KMEPR – искомое.
K
М
A1
В1
С1
A
В
С
D
E
Р
N
R
Почему строим МЕ?
Зачем нужна вспомогательная плоскость?
Почему Р∈AD?
Почему строим KN||РЕ?
Как по-другому можно было построить точку Р?
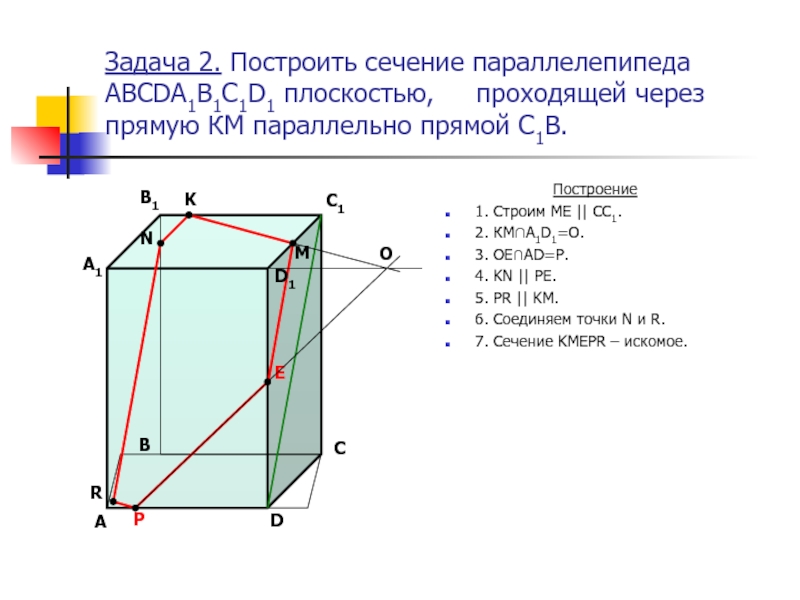
Слайд 4Задача 2. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через
Построение
1. Строим МЕ || CC1.
2. КМ∩А1D1=O.
3. OE∩AD=P.
4. KN || PE.
5. PR || KM.
6. Соединяем точки N и R.
7. Сечение KMEPR – искомое.
K
М
A1
В1
С1
A
В
С
D
E
Р
N
R
O
D1