- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сечение тел плоскостью презентация
Содержание
- 1. Сечение тел плоскостью
- 2. Примеры сечения Продольное сечение детали.
- 3. ОПРЕДЕЛЕНИЕ Сечением поверхности геометрических тел
- 4. Построить сечение многогранника плоскостью –
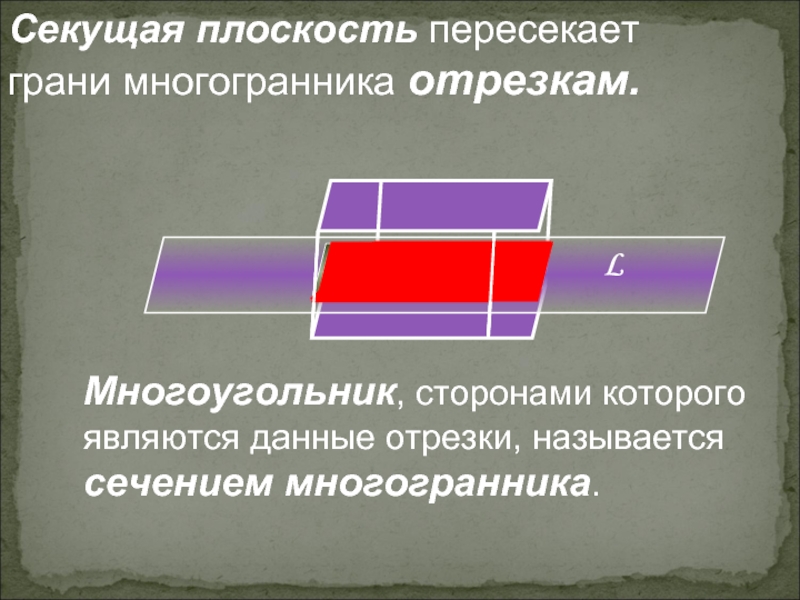
- 5. Секущая плоскость пересекает грани многогранника отрезкам. Многоугольник, сторонами которого являются данные отрезки, называется сечением многогранника.
- 6. Секущая плоскость пересекает грани многогранника по
- 7. Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.
- 8. 1. Соединять можно только две точки, лежащие
- 9. Какие многоугольники могут получиться в сечении
- 10. Треугольники Параллелепипед имеет 6 граней Четырехугольники
- 11. Аксиоматический метод
- 12. Вершины сечения находятся только на ребрах.
Примеры сечения Продольное сечение детали.
Слайд 3ОПРЕДЕЛЕНИЕ
Сечением поверхности геометрических тел плоскостью называется плоская фигура, полученная
в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости.
Слайд 4 Построить сечение многогранника плоскостью – это значит указать точки
пересечения секущей плоскости с ребрами многогранника и соединить эти точки отрезками, принадлежащими граням многогранника.
Для построения сечения многогранника плоскостью нужно в плоскости каждой грани указать 2 точки, принадлежащие сечению, соединить их прямой и найти точки пересечения этой прямой с ребрами многогранника.
Для построения сечения многогранника плоскостью нужно в плоскости каждой грани указать 2 точки, принадлежащие сечению, соединить их прямой и найти точки пересечения этой прямой с ребрами многогранника.
Слайд 5Секущая плоскость пересекает грани многогранника отрезкам.
Многоугольник, сторонами которого являются данные отрезки,
называется сечением многогранника.
Слайд 6
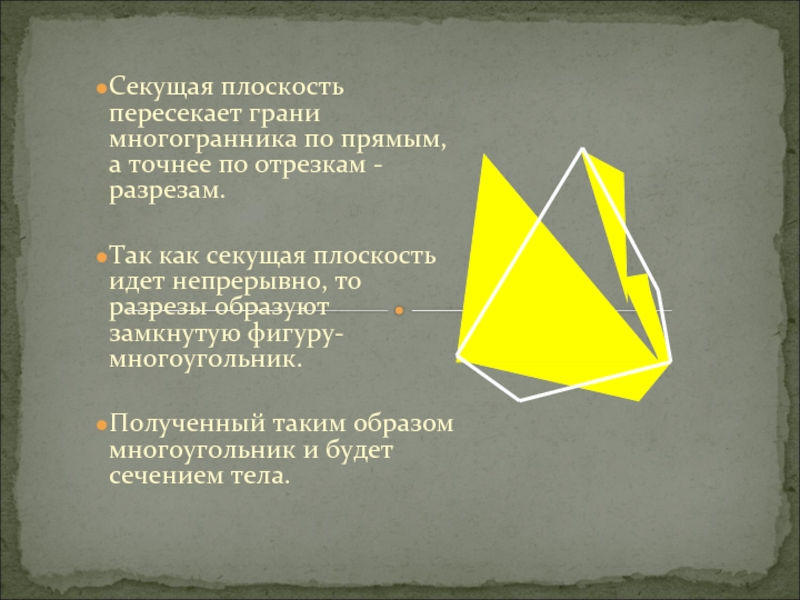
Секущая плоскость пересекает грани многогранника по прямым, а точнее по отрезкам
- разрезам.
Так как секущая плоскость идет непрерывно, то разрезы образуют замкнутую фигуру-многоугольник.
Полученный таким образом многоугольник и будет сечением тела.
Так как секущая плоскость идет непрерывно, то разрезы образуют замкнутую фигуру-многоугольник.
Полученный таким образом многоугольник и будет сечением тела.
Слайд 7Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.
Слайд 81. Соединять можно только две точки, лежащие
в плоскости одной грани.
При этом
необходимо учитывать следующее:
Для построения сечения нужно построить точки пересечения секущей плоскости с ребрами и соединить их отрезками.
2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.
Слайд 9
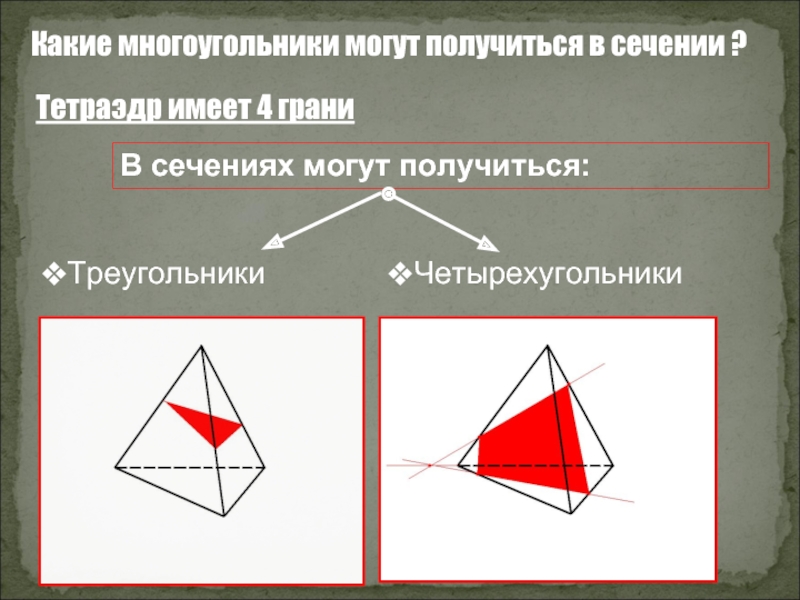
Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В сечениях
могут получиться:
Четырехугольники
Треугольники
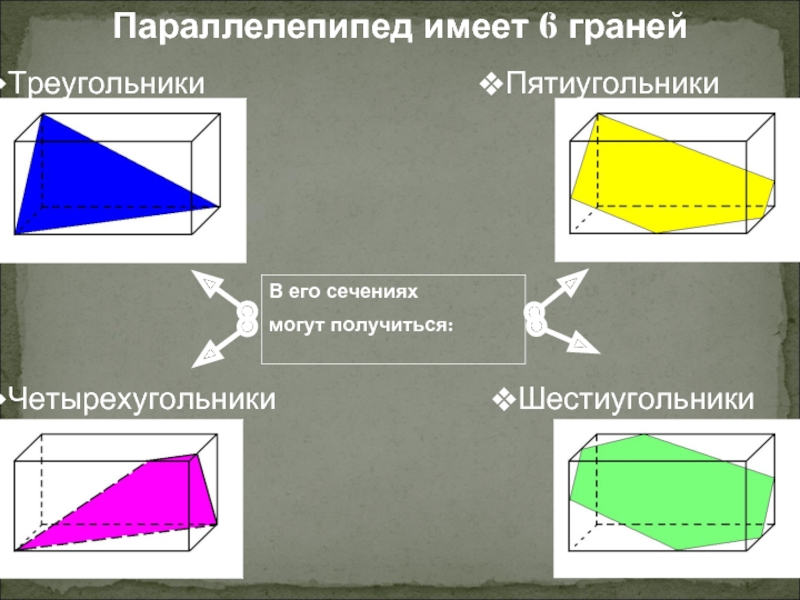
Слайд 10Треугольники
Параллелепипед имеет 6 граней
Четырехугольники
Шестиугольники
Пятиугольники
В его сечениях
могут получиться:
Слайд 11 Аксиоматический метод
Метод следов
Суть метода заключается в построении
вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры .
Слайд 12Вершины сечения находятся только на ребрах.
Стороны сечения находятся только на гранях
многогранника.
Секущая плоскость пересекает грань или плоскость грани только один раз.
Секущая плоскость пересекает грань или плоскость грани только один раз.
