Выразим коэффициенты ряда через f(x). Найдем производные функции f(x), почленно дифференцируя n раз:
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Ряд Маклорена. (Тема 14.3) презентация
Содержание
- 1. Ряд Маклорена. (Тема 14.3)
- 2. Если в полученных выражениях положить х=0, то получим:
- 3. Отсюда находим коэффициенты ряда:
- 4. Подставляем найденные коэффициенты в разложение функции в ряд:
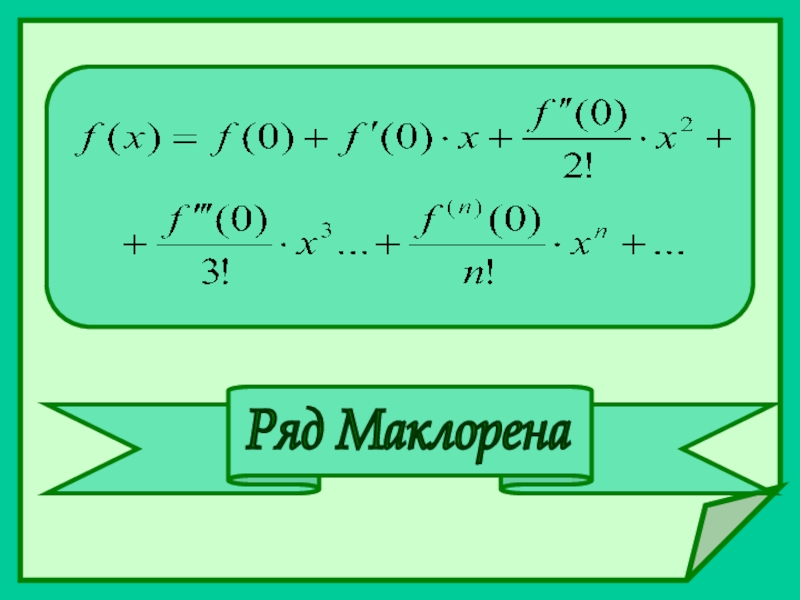
- 5. Ряд Маклорена
- 6. Так же, как и для числовых
- 7. Теорема Для того, чтобы ряд
- 8. Можно доказать, что если функция f(x)
- 9. Ряд Тейлора
- 10. Ряд Тейлора связан с формулой Тейлора: Формула Тейлора
- 11. остаточный член формулы Тейлора
- 12. Если То остаток ряда Тейлора равен остаточному члену формулы Тейлора:
Если в полученных выражениях положить х=0, то получим:
Слайд 1
14.3. РЯД МАКЛОРЕНА
Предположим, что функция y=f(x) определена и n раз дифференцируема
в окрестности точки х=0, и может быть представлена в виде суммы степенного ряда, т.е. может быть разложена в степенной ряд:
Слайд 6
Так же, как и для числовых рядов, сумму f(x) ряда Маклорена
можно представить в виде
где
- n–ая частичная сумма ряда;
- n–ый остаток ряда.
Слайд 7
Теорема
Для того, чтобы ряд Маклорена сходился к функции f(x), необходимо и
достаточно, чтобы при
остаток ряда стремился к нулю, т.е.
для всех х из области сходимости ряда.
Слайд 8
Можно доказать, что если функция f(x) разложима в ряд Маклорена, то
это разложение единственно.
Замечание
Ряд Маклорена является частным случаем ряда
Тейлора при х0=0
