- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Розвязування задач на властивість пірамід презентация
Содержание
- 1. Розвязування задач на властивість пірамід
- 2. Визначення Пірамідою є багатогранник, одна грань якого
- 3. З історії означень
- 4. Элементи піраміди МО – висота МН –
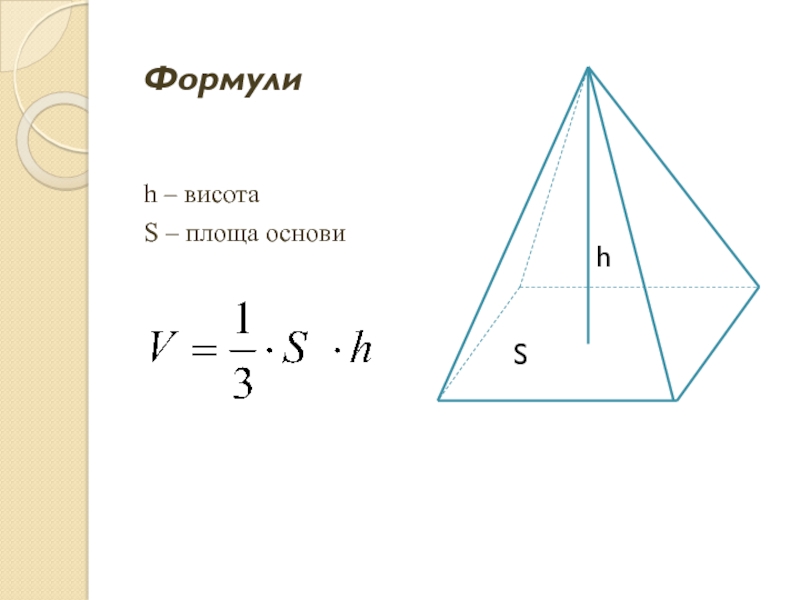
- 5. Формули h – висота S – площа основи
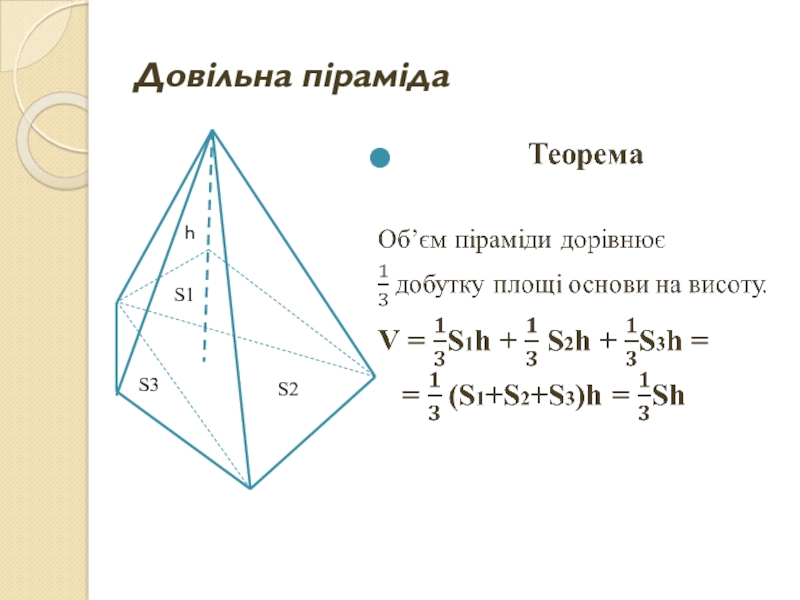
- 6. Довільна піраміда
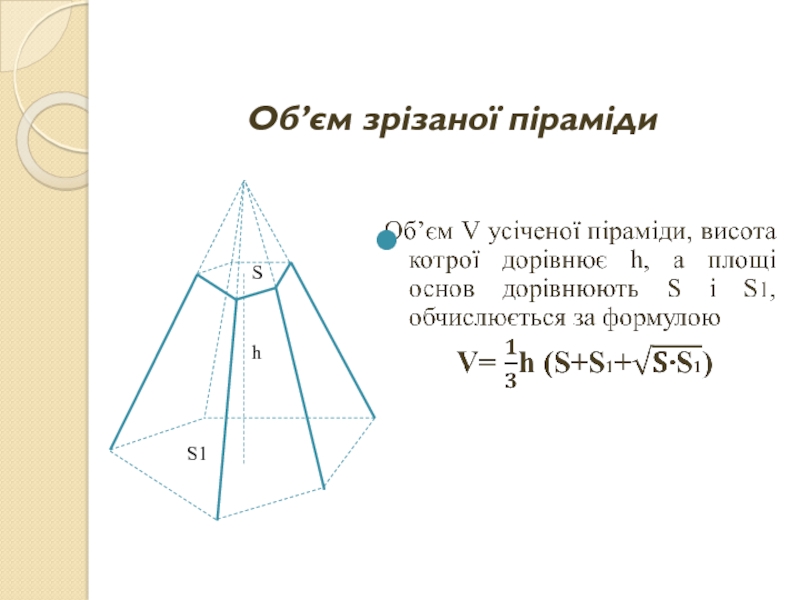
- 7. Об’єм зрізаної піраміди
- 8. У правильній чотирикутній
- 9. РОЗВ’ЯЗАННЯ
- 10. №1 Плоский кут при вершині правильної чотирикутної
- 11. В основі піраміди лежить
- 12. РОЗВ’ЯЗАННЯ
- 13. В основі піраміди лежить
- 14. РОЗВ’ЯЗАННЯ
- 15. РОЗВ’ЯЖІТЬ №1 В
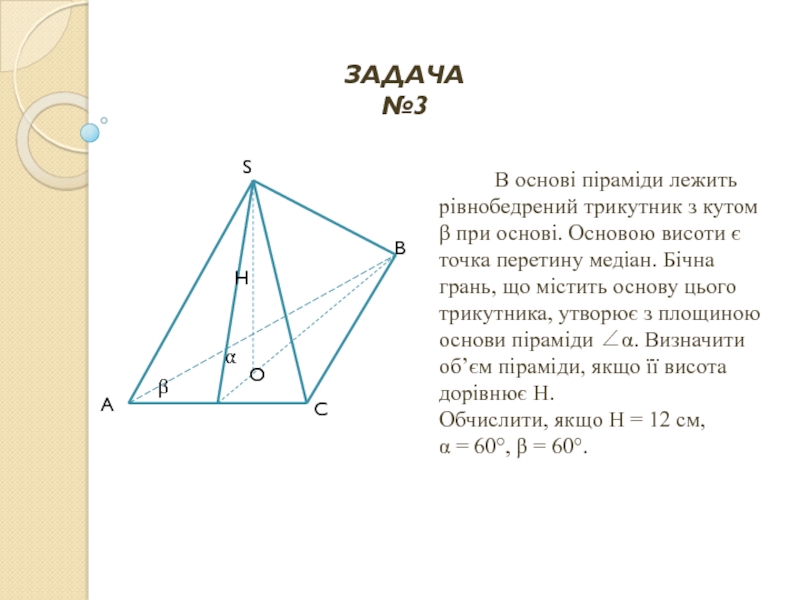
- 16. В основі піраміди лежить рівнобедрений трикутник з
- 17. Примітка: Якщо в деякій піраміді
- 18. В основі піраміди лежить трикутник з кутами
- 19. РОЗВ’ЯЗАННЯ
- 20. РОЗВ’ЯЖІТЬ №2
- 21. В основі піраміди лежить рівнобедрений трикутник з
- 22. РОЗВ’ЯЗАННЯ
- 23. Примітка: Якщо в деякій піраміді
- 24. Апофема правильної чотирикутної піраміди дорівнює m.
- 25. РОЗВ’ЯЗАННЯ
- 26. В основі піраміди лежить прямокутний трикутник з
- 27. РОЗВ’ЯЗАННЯ
- 28. №1 У правильній трикутній
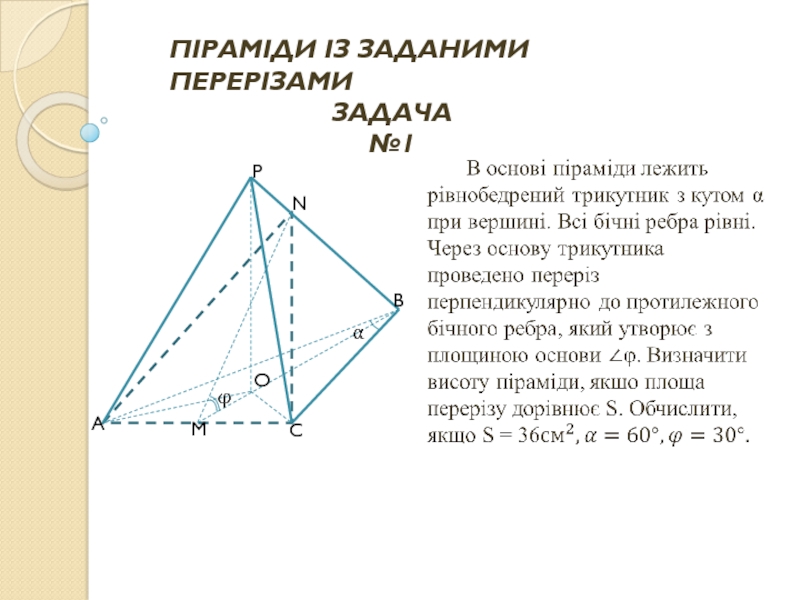
- 29. ПІРАМІДИ ІЗ ЗАДАНИМИ ПЕРЕРІЗАМИ ЗАДАЧА №1
- 30. РОЗВ’ЯЗАННЯ
- 31.
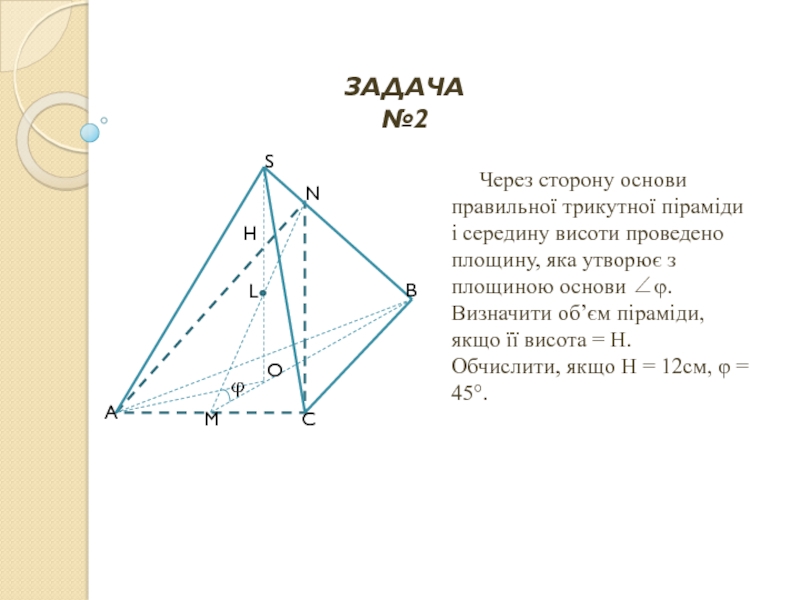
- 32. Через сторону основи правильної
- 33. РОЗВ’ЯЗАННЯ
- 34. РОЗВ’ЯЖІТЬ
- 35. ПІРАМІДИ, В ЯКИХ ЗАДАНА ВІДСТАНЬ ВІД ОСНОВИ
- 36. РОЗВ’ЯЗАННЯ
- 37. Примітка: Якщо в деякій піраміді всі
- 38. У правильній трикутній
- 39. РОЗВ’ЯЗАННЯ
- 40. №1 У правильній трикутній піраміді бічне ребро
- 41. В основі піраміди лежить рівнобедрений трикутник з
- 42. РОЗВ’ЯЗАННЯ
- 43.
- 44. Примітка 2: Якщо бічні грані піраміди утворюють
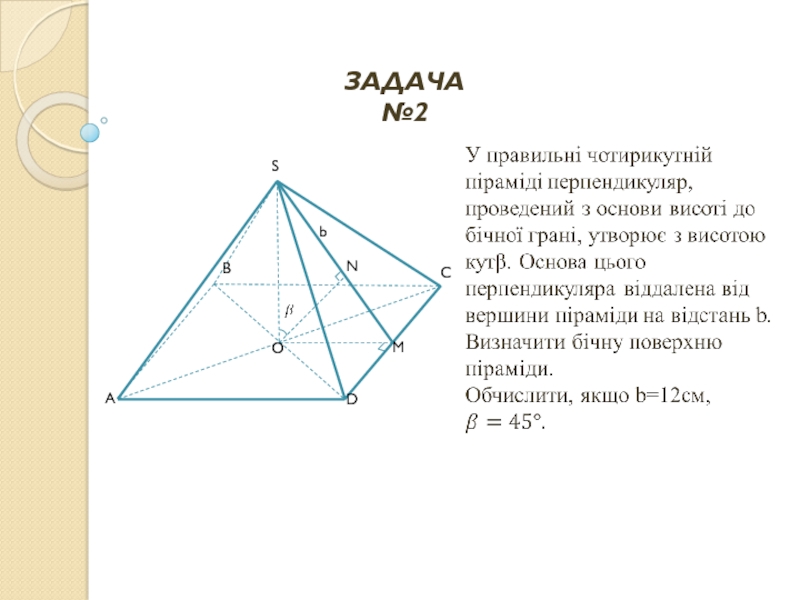
- 45. ЗАДАЧА №2
- 46. РОЗВ’ЯЗАННЯ
- 47. №1 В основі піраміди лежить рівнобедрений трикутник
- 48. В основі
- 49. РОЗВ’ЯЗАННЯ
- 50. Дякуємо за увагу!
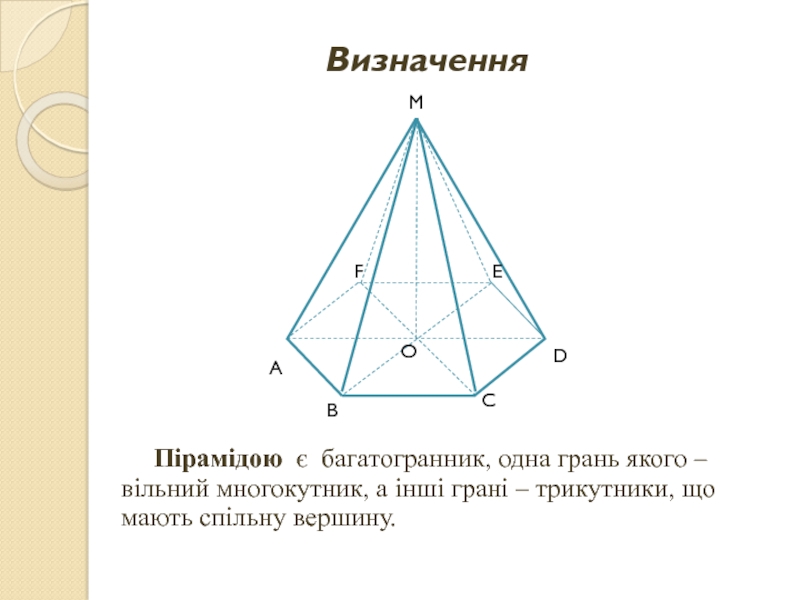
Слайд 2Визначення
Пірамідою є багатогранник, одна грань якого – вільний многокутник, а інші
Слайд 3З історії означень
Евклід визначає піраміду як тілесну фігуру, обмежену площинами, котрі від однієї площини (основи) збігаються в єдиній точці(вершині).
Герон дає наступне визначення піраміди: це фігура обмежена трикутниками, що збігаються в одній точці, і основою якої є многокутник.
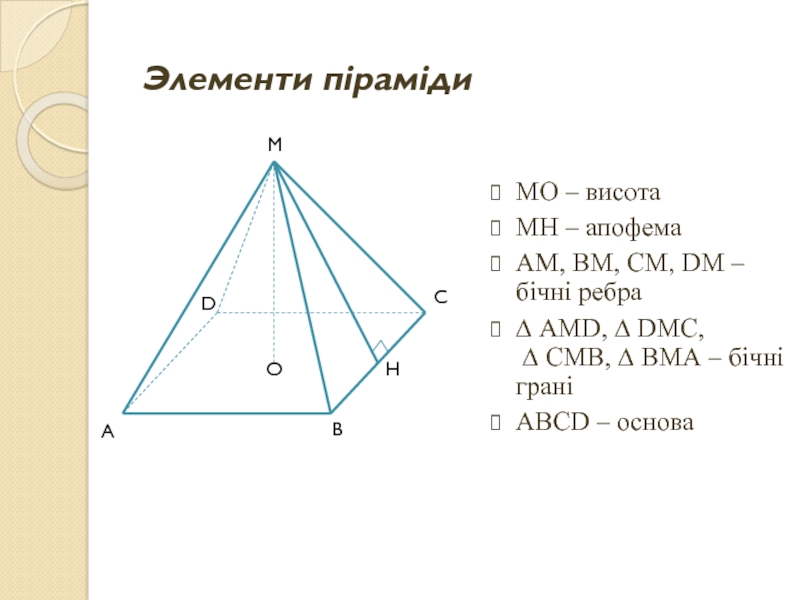
Слайд 4Элементи піраміди
МО – висота
МН – апофема
АМ, ВМ, СМ, DМ – бічні
∆ АМD, ∆ DМС, ∆ СМВ, ∆ ВМА – бічні грані
АВСD – основа
A
B
H
C
O
D
M
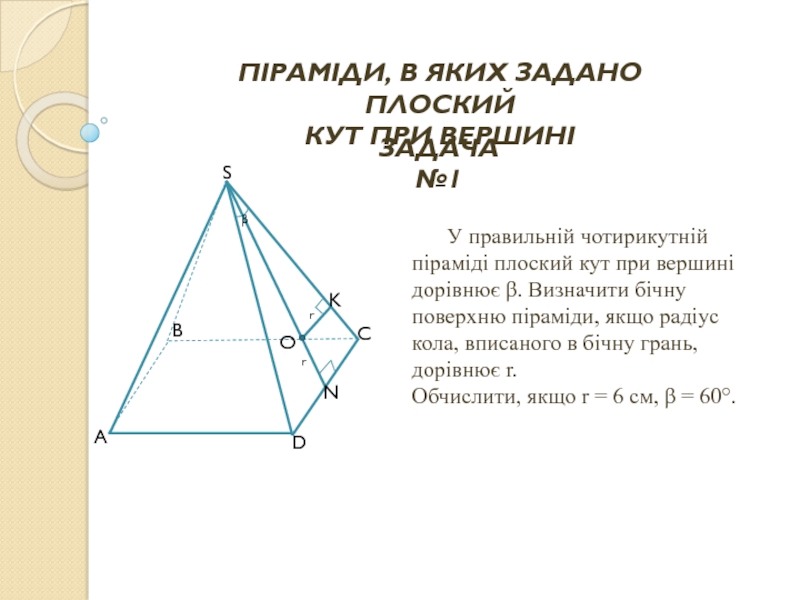
Слайд 8 У правильній чотирикутній піраміді плоский кут при
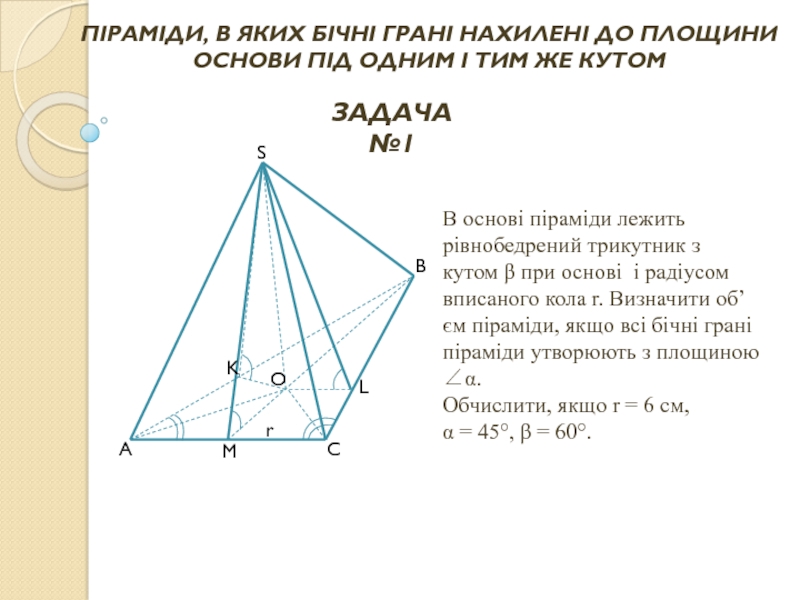
Обчислити, якщо r = 6 см, β = 60°.
ПІРАМІДИ, В ЯКИХ ЗАДАНО ПЛОСКИЙ
КУТ ПРИ ВЕРШИНІ
ЗАДАЧА №1
Слайд 10№1
Плоский кут при вершині правильної чотирикутної піраміди дорівнює β. Визначити повну
№2
У правильній трикутній піраміді плоский кут при вершині дорівнює φ. Визначити бічну поверхню піраміди, якщо радіус вписаного в бічну грань кола дорівнює r. Обчислити, якщо r = 6см, φ = 60°.
№3
У правильній трикутній піраміді плоский кут при вершині дорівнює α. Визначити бічну поверхню піраміди, якщо радіус кола, описаного навколо бічної грані, дорівнює R. Обчислити, якщо R = 12 cм,
α = 60°.
РОЗВ’ЯЖІТЬ ЗАДАЧІ
Слайд 11 В основі піраміди лежить рівнобедрений трикутник з основою
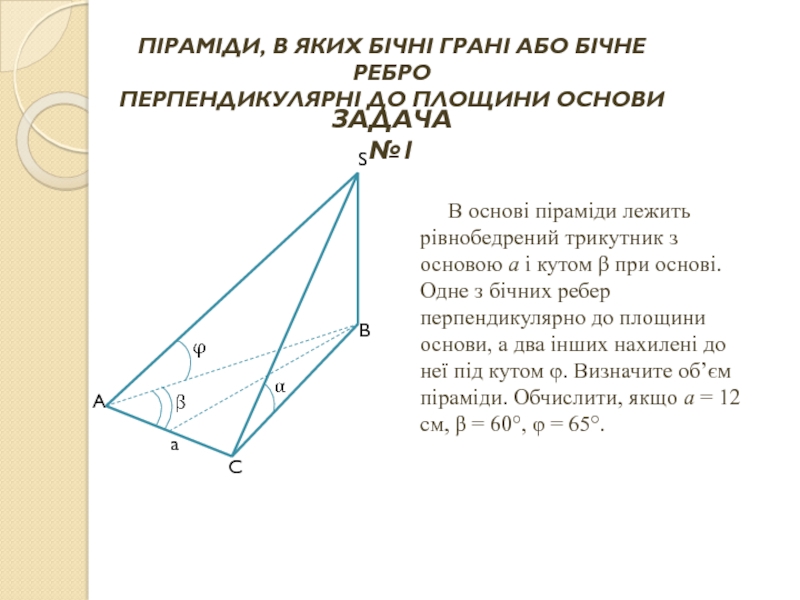
ПІРАМІДИ, В ЯКИХ БІЧНІ ГРАНІ АБО БІЧНЕ РЕБРО
ПЕРПЕНДИКУЛЯРНІ ДО ПЛОЩИНИ ОСНОВИ
ЗАДАЧА №1
Слайд 13 В основі піраміди лежить прямокутний трикутник з кутом
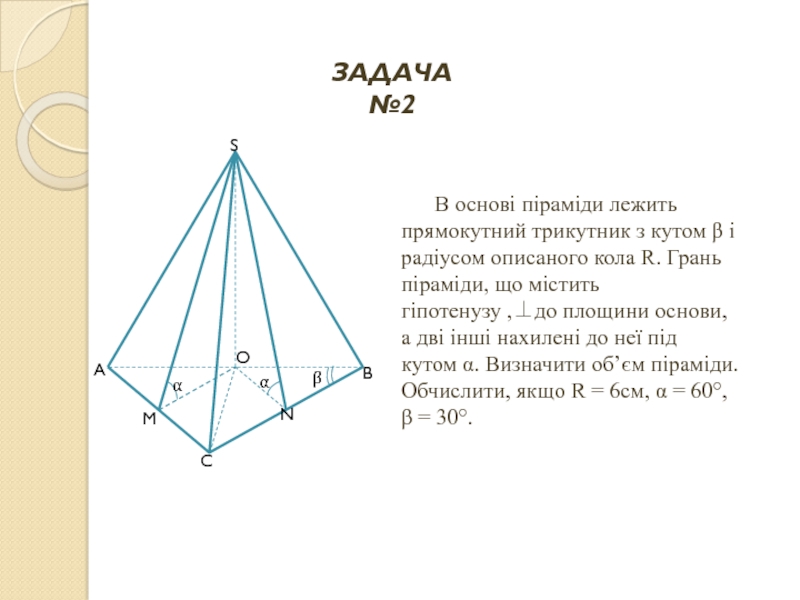
ЗАДАЧА №2
Слайд 15РОЗВ’ЯЖІТЬ
№1
В основі піраміди лежить правильний трикутник з
r = 6см, α = 60°.
№2
В основі піраміди лежить рівнобедрений трикутник з кутом α при вершині. Одне з бічних ребер перпендикулярне до площини основи, а два інших дорівнюють b і утворюють з основою ∠φ. Визначити об’єм піраміди. Обчислити якщо b = 12 см, α = 60°, φ = 45°.
№3
В основі піраміди лежить правильний трикутник з стороною a. Одна грань піраміди перпендикулярна до площини основи, а дві інші нахилені до неї під кутом α . Визначити об’єм цієї піраміди. Обчислити, якщо а = 6см,
α = 60°.
Слайд 16 В основі піраміди лежить рівнобедрений трикутник з кутом α при основі
ПІРАМІДИ, В ЯКИХ БІЧНІ РЕБРА НАХИЛЕНІ ДО ПЛОЩИНИ ОСНОВИ ПІД ОДНИМ І ТИМ ЖЕ КУТОМ
ЗАДАЧА №1
Слайд 17
Примітка: Якщо в деякій піраміді всі бічні ребра рівні між
РОЗВ’ЯЗАННЯ
Слайд 18 В основі піраміди лежить трикутник з кутами α і β. Всі
ЗАДАЧА №2
Слайд 20РОЗВ’ЯЖІТЬ
№2
В основі піраміди лежить трикутник зі стороною
Обчислити, якщо c = 12 см, α = 30°, β = 60°, φ = 45°.
Слайд 21В основі піраміди лежить рівнобедрений трикутник з кутом β при основі
α = 45°, β = 60°.
ПІРАМІДИ, В ЯКИХ БІЧНІ ГРАНІ НАХИЛЕНІ ДО ПЛОЩИНИ ОСНОВИ ПІД ОДНИМ І ТИМ ЖЕ КУТОМ
ЗАДАЧА №1
Слайд 23
Примітка: Якщо в деякій піраміді всі бічні грані утворюють з
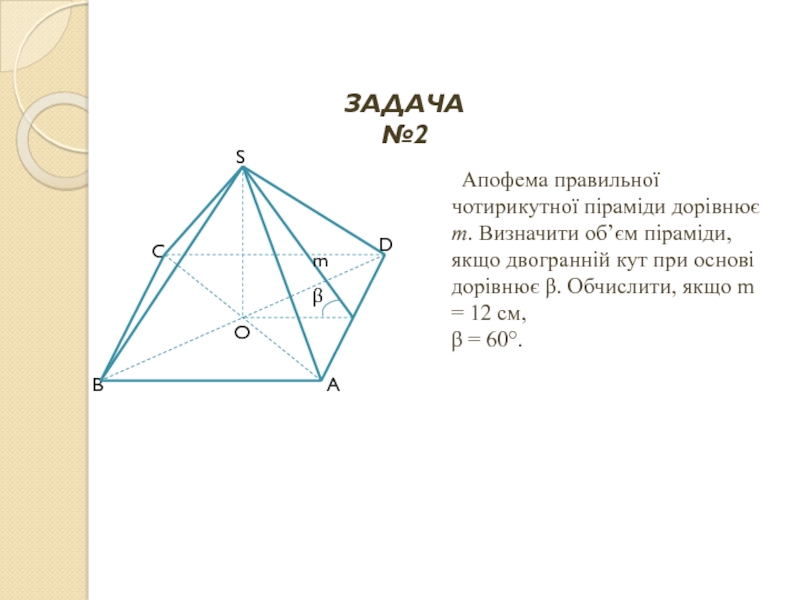
Слайд 24 Апофема правильної чотирикутної піраміди дорівнює m. Визначити об’єм піраміди, якщо
β = 60°.
ЗАДАЧА №2
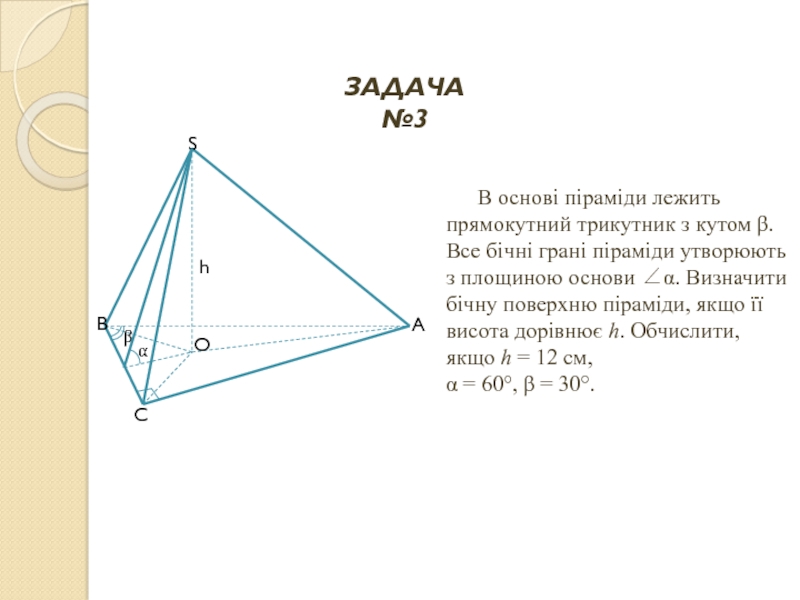
Слайд 26В основі піраміди лежить прямокутний трикутник з кутом β. Все бічні
α = 60°, β = 30°.
ЗАДАЧА №3
Слайд 28№1
У правильній трикутній піраміди радіус описаного навколо основи
№2
Апофема правильної трикутної піраміди дорівнює l. Визначити об’єм піраміди, якщо двогранний кут при основі дорівнює β. Обчислити, якщо l = 18 см, β = 60°.
РОЗВ’ЯЖІТЬ
Слайд 32 Через сторону основи правильної трикутної піраміди і середину
ЗАДАЧА №2
Слайд 35ПІРАМІДИ, В ЯКИХ ЗАДАНА ВІДСТАНЬ ВІД ОСНОВИ ВИСОТИ ДО БІЧНОГО РЕБРА
В основі піраміди лежить рівнобедрений трикутник з кутом α при основі. Всі бічні ребра піраміди нахилені до площини основи під кутом β. Визначити об’єм піраміди, якщо відстань від основи висоти до бічного ребра дорівнює l. Обчислити, якщо l = 18 см, α = 60°, β = 60°.
ЗАДАЧА №1
Слайд 37
Примітка: Якщо в деякій піраміді всі бічні ребра рівні або якщо
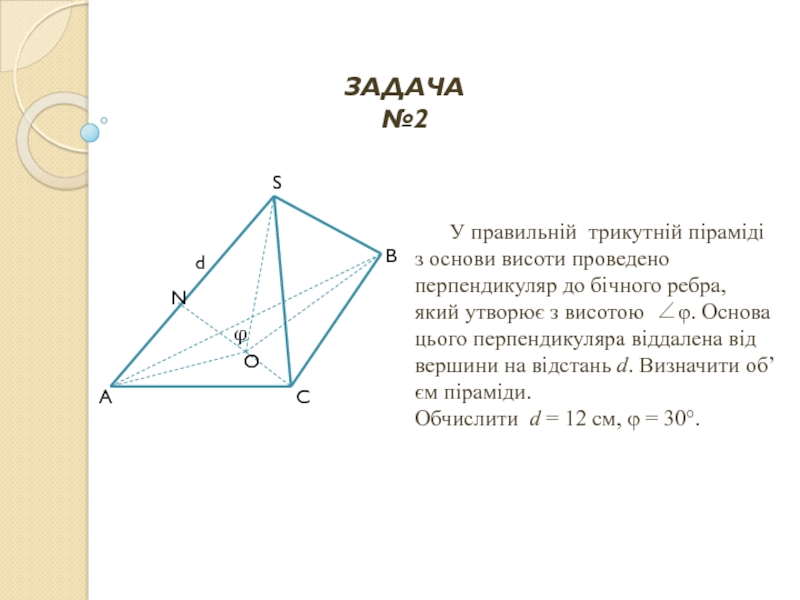
Слайд 38 У правильній трикутній піраміді з основи висоти
ЗАДАЧА №2
Слайд 40№1
У правильній трикутній піраміді бічне ребро утворює з площиною основи ∠α.
№2
У правильній трикутній піраміді з основи висоти проведено перпендикуляр до бічного ребра, який утворює з площиною ∠φ. Довжина цього перпендикуляра дорівнює а. Визначити об’єм піраміди. Обчислити, якщо а = 18см, і φ = 30°.
№3
В основі піраміди лежить прямокутник з кутом α між діагоналями. Всі бічні ребра піраміди нахилені до площини основи під кутом β. Визначити об’єм піраміди, якщо відстань від основи висоти до бічного ребра дорівнює а. Обчислити, якщо а = 12см, α = 60°, β = 60°.
РОЗВ’ЯЖІТЬ
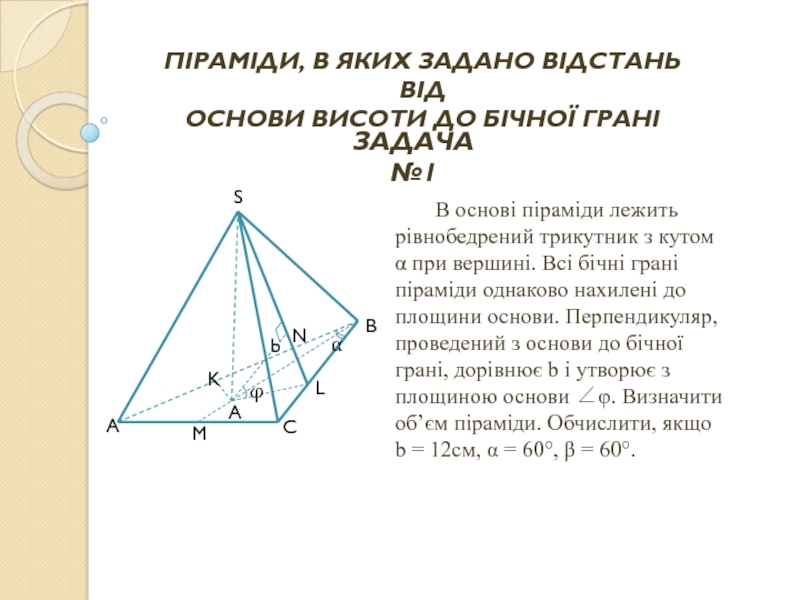
Слайд 41 В основі піраміди лежить рівнобедрений трикутник з кутом α при вершині.
ПІРАМІДИ, В ЯКИХ ЗАДАНО ВІДСТАНЬ ВІД
ОСНОВИ ВИСОТИ ДО БІЧНОЇ ГРАНІ
ЗАДАЧА №1
Слайд 44Примітка 2: Якщо бічні грані піраміди утворюють з площиною основи один
Примітка 1: Якщо з основи висоти піраміди опустити перпендикуляр до бічної грані, то основа цього перпендикуляра лежить на висоті даної грані, проведеній з вершини піраміди. Кут між перпендикуляром і площиною основи дорівнює куту між перпендикуляром і проекцією зазначеної висоти на площину основи.
Слайд 47№1
В основі піраміди лежить рівнобедрений трикутник з кутом β при основі.
№2
В основі піраміди лежить ромб з гострим кутом α. Точка перетину діагоналей ромба є основою висоти, з якої до бічної грані проведено перпендикуляр, який утворює з площиною ∠φ. Визначити бічну поверхню піраміди, якщо довжина цього перпендикуляра дорівнює а. Обчислити, якщо а = 12 см, α = 60°, φ = 30°.
№3
В основі піраміди лежить прямокутний трикутник з кутом β. Основою висоти піраміди є вершина іншого гострого кута трикутника, з якої проведено перпендикуляр до протилежної бічної грані. Цей перпендикуляр утворює висотою піраміди ∠φ, а його основа віддалена від вершини піраміди на відстань b. Визначити об’єм піраміди. Обчислити, якщо b = 12 см, α = 60°, φ = 30°.
РОЗВ’ЯЖІТЬ
Слайд 48 В основі піраміди лежить рівнобедрений трикутник
ЗАДАЧА №3