- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач с помощью графов презентация
Содержание
- 1. Решение задач с помощью графов
- 2. Домашнее задание «Применение графа»
- 3. ВСПОМНИМ… Граф Простейшая модель системы.Отображает элементарный состав
- 4. Кенигсбергские мосты
- 5. Кенигсбергские мосты Можно ли обойти все Кенигсбергские
- 6. Представим задачу в виде графа,где вершины –
- 7. Какие вершины четные, а какие нечетные? Подпишем
- 8. Если граф имеет цикл, содержащий все ребра
- 9. Алгоритм решения задач 1. Нарисовать граф, где
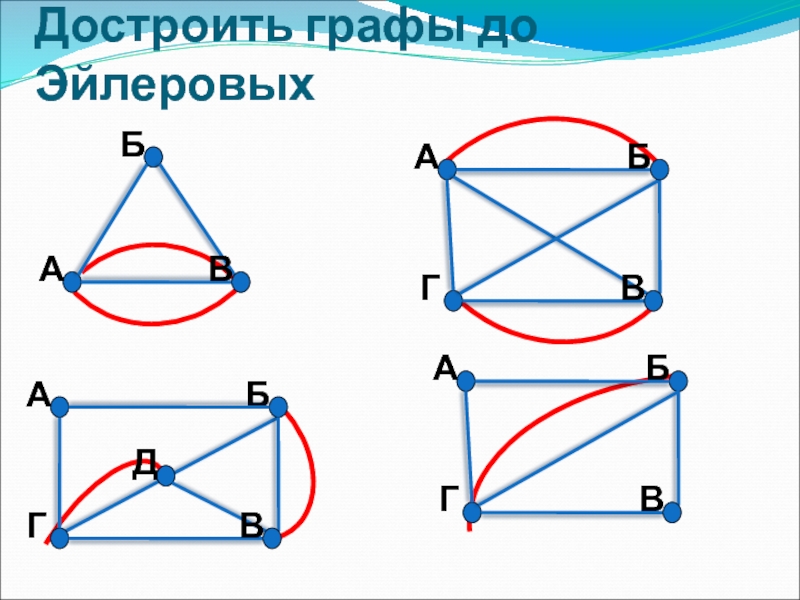
- 10. Достроить графы до Эйлеровых
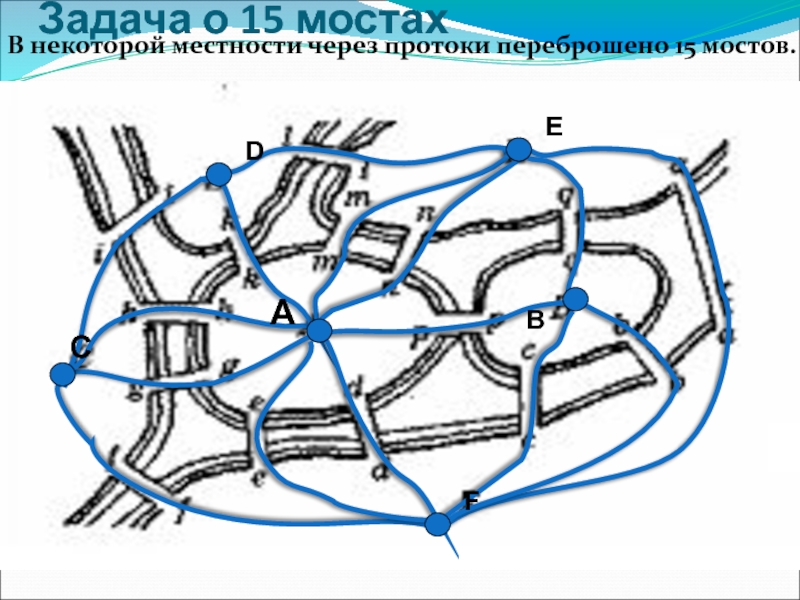
- 11. Задача о 15 мостах В некоторой местности
- 12. Построим граф, где вершины – острова и
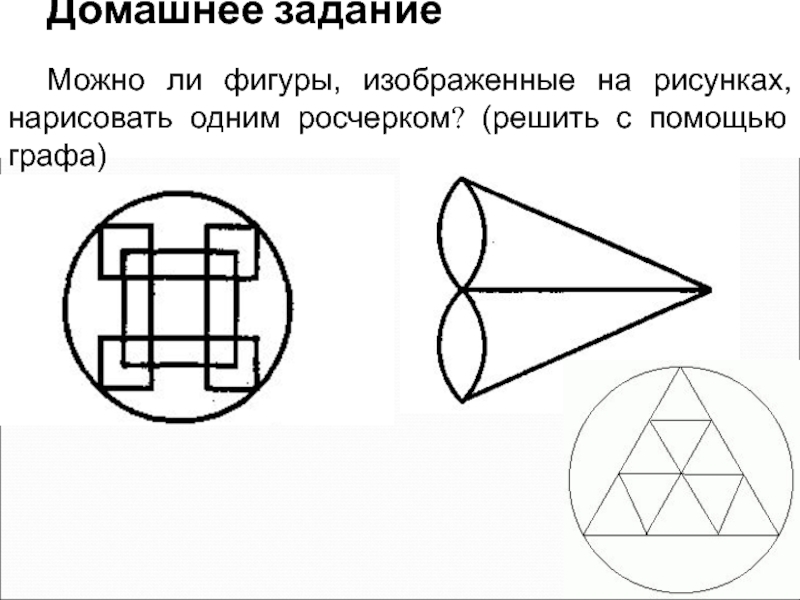
- 13. Домашнее задание Можно ли фигуры, изображенные
Слайд 3ВСПОМНИМ…
Граф
Простейшая модель системы.Отображает элементарный состав системы и структуру связей
Сеть
Граф с возможностью
Граф называется связным
если любая пара его вершин — связная.
Ребро соединяет две вершины графа
элемент (точка) графа, обозначающий объект любой природы, входящий в множество объектов, описываемое графом
Вершина
Ребро
это ориентированное ребро.
Дуга
ребро, начало и конец которого находятся в одной и той же вершине
Петля
любой связный граф, не имеющий циклов.
Дерево
Слайд 5Кенигсбергские мосты
Можно ли обойти все Кенигсбергские мосты, проходя только один раз
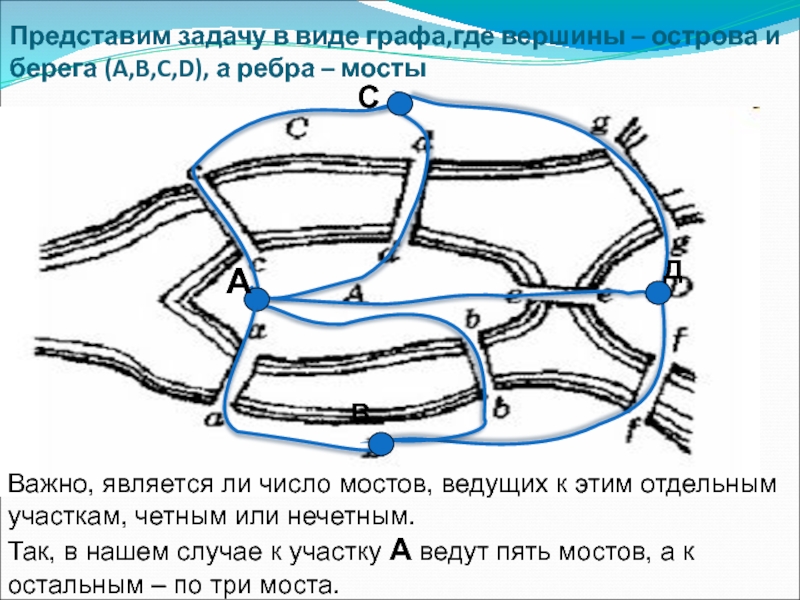
Слайд 6Представим задачу в виде графа,где вершины – острова и берега (A,B,C,D),
Важно, является ли число мостов, ведущих к этим отдельным участкам, четным или нечетным.
Так, в нашем случае к участку A ведут пять мостов, а к остальным – по три моста.
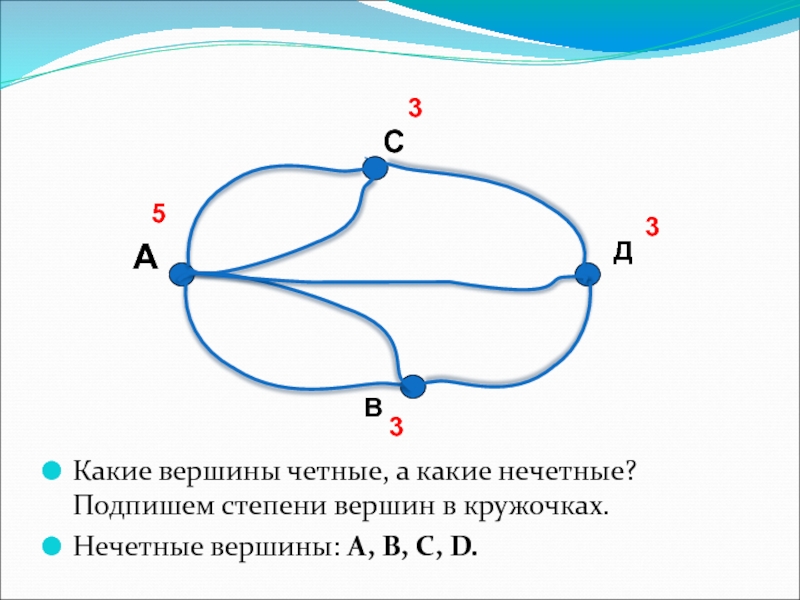
Слайд 7Какие вершины четные, а какие нечетные? Подпишем степени вершин в кружочках.
Нечетные
3
3
3
5
Слайд 8Если граф имеет цикл, содержащий все ребра графа по одному разу
Условия существования Эйлеровой линии:
-граф связный
-все вершины четные
Другими словами, эйлеров граф – это граф,который можно нарисовать одним росчерком
Эйлеров граф
Слайд 9Алгоритм решения задач
1. Нарисовать граф, где вершины – острова и берега,
2. Определить степень каждой вершины и подписать возле нее.
3. Посчитать количество нечетных вершин.
4. Обход возможен:
a. ЕСЛИ все вершины – четные, и его можно начать с любого участка.
b. ЕСЛИ 2 вершины – нечетные, но его нужно начать с одной из нечетных местностей.
5. Обход невозможен, если нечетных вершин больше 2.
6. Сделать ВЫВОД.
7. Указать Начало и Конец пути.
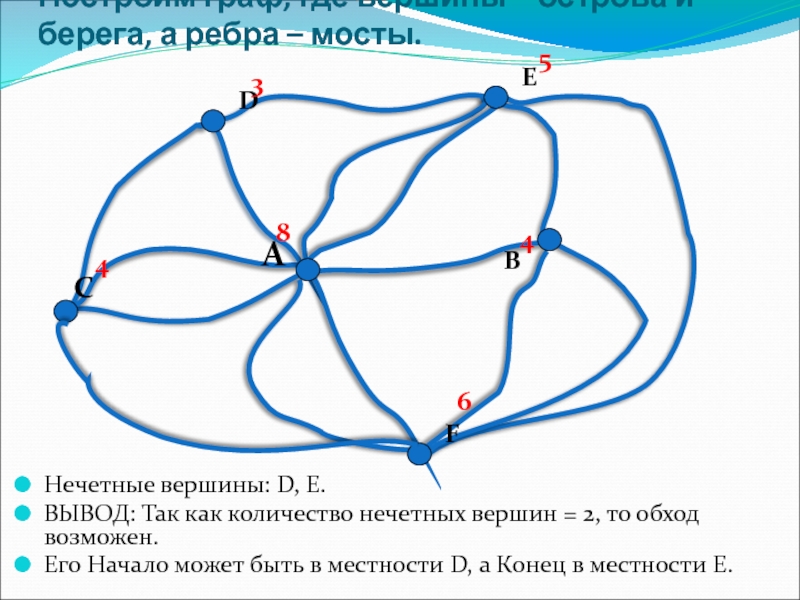
Слайд 12Построим граф, где вершины – острова и берега, а ребра –
Нечетные вершины: D, E.
ВЫВОД: Так как количество нечетных вершин = 2, то обход возможен.
Его Начало может быть в местности D, а Конец в местности E.
4
4
6
3
5
8