- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение уравнений и неравенств, содержащих переменную под знаком модуля презентация
Содержание
Слайд 72. Решение упражнений.
1. Упростите выражение:
2. Упростите выражение:
3. Доказать, что данное
Слайд 39ГЛАВА III. НЕРВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ, СОДЕРЖАЩИЕ МОДУЛЬ, НА КООРДИНАТНОЙ ПЛОСКОСТИ.
Занятие
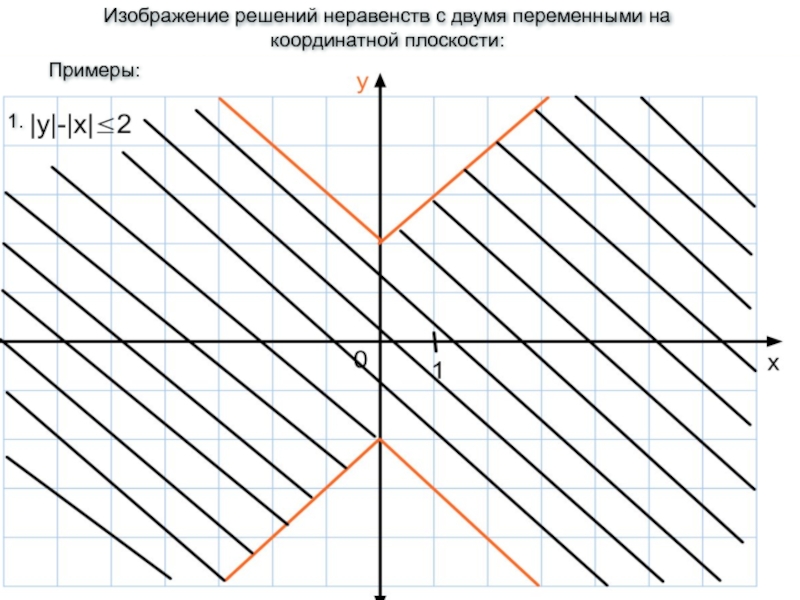
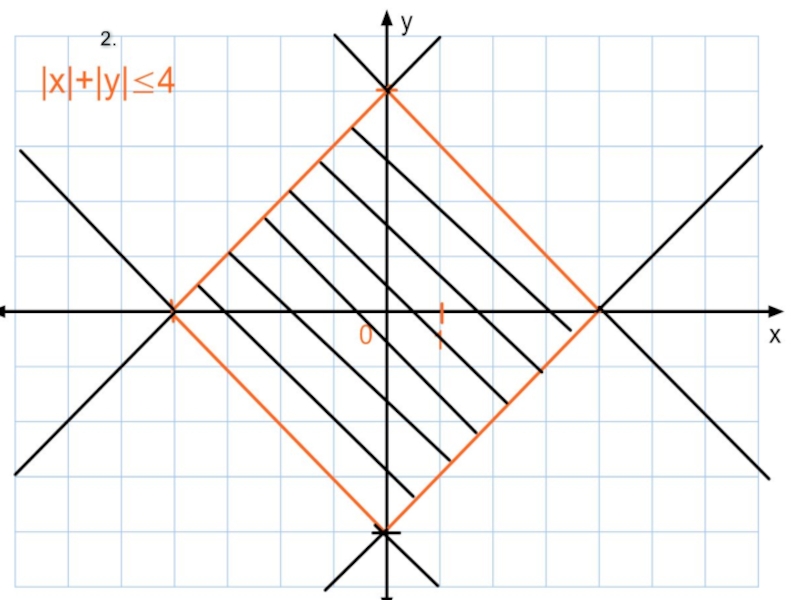
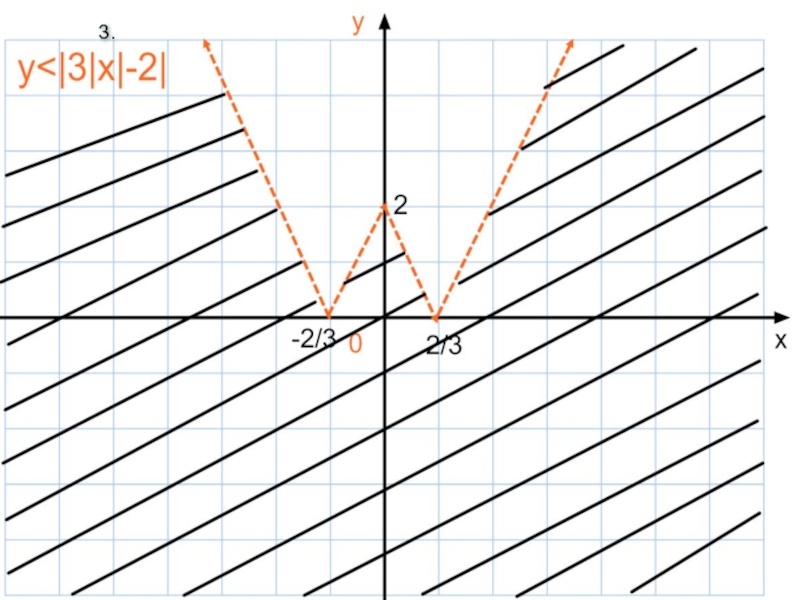
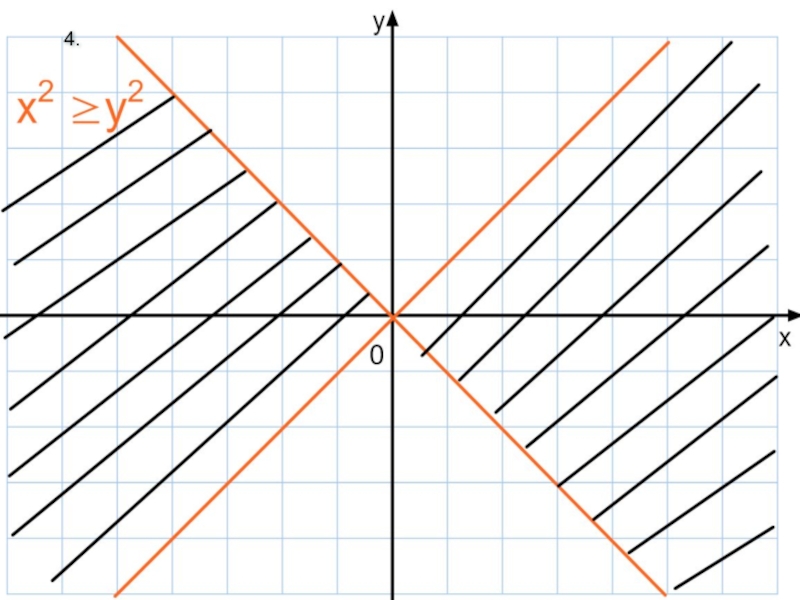
Геометрическая интерпретация уравнений вида |x-a|+|x-b|=c и |x-a|-|x-b|=c. Изображение фигур на плоскости, задаваемых неравенствами.
ЦЕЛЬ: научить изображать на плоскости фигуры, расширить представления учащихся о взаимосвязи между алгебраическими соотношения и их геометрическими образами на координатными плоскостями.
Методические рекомендации:
Необходимо использовать рассматриваемый материал, включающий эстетический компонент, для развития интереса к предмету, а также для более глубокого усвоения базовых знаний. Кроме того, важно, чтобы учащимися были предложены задания, аппелирующие к воображению, фантазии.
Слайд 40Уравнения |х-а|+|х-в|=с и |х-а|-|х-в|=с имеют простую геометрическую интерпретацию.
Рассмотрим уравнение|х-2|+|х+3|=7.
Решить это уравнение
Внутри отрезка [-3;2] таких точек нет, так как длина отрезка |2-(-3)|=5<7.Значит эти точки лежат вне отрезка.
Легко видеть, что эти точки (-4) и (3).Следовательно,х=-4,х=3-корни уравнения.
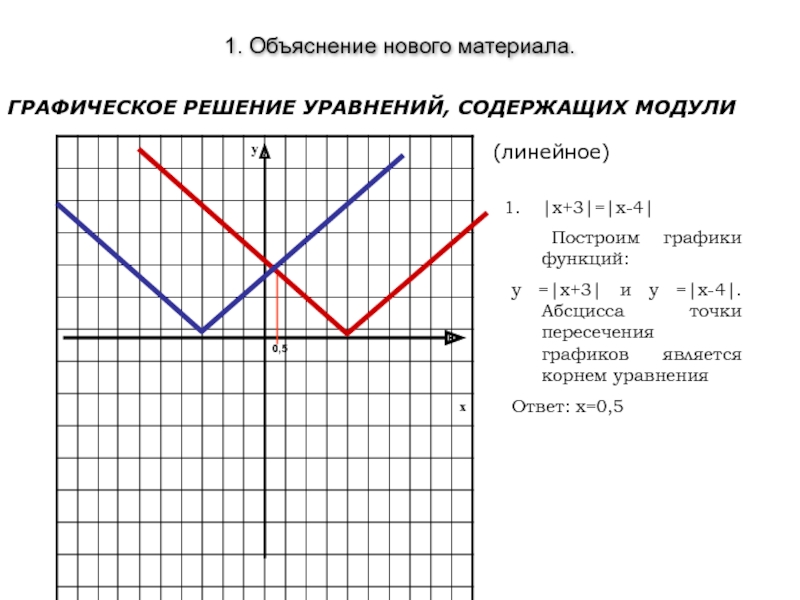
1. Объяснение нового материала