- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение треугольников презентация
Содержание
- 1. Решение треугольников
- 2. 10/03/2019
- 3. 10/03/2019 Определение Решением треугольника называется нахождение всех
- 4. 10/03/2019 Для этого вспомним Решение данных задач
- 5. 10/03/2019 А В С
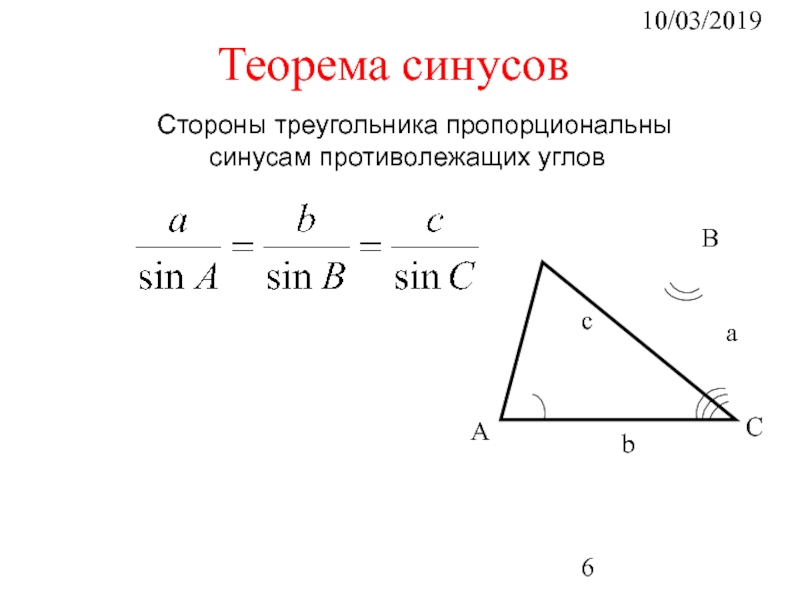
- 6. 10/03/2019 Стороны треугольника пропорциональны синусам противолежащих углов Теорема синусов
- 7. 10/03/2019 Квадрат стороны треугольника равен сумме квадратов
- 8. 10/03/2019 Три задачи на решение треугольника
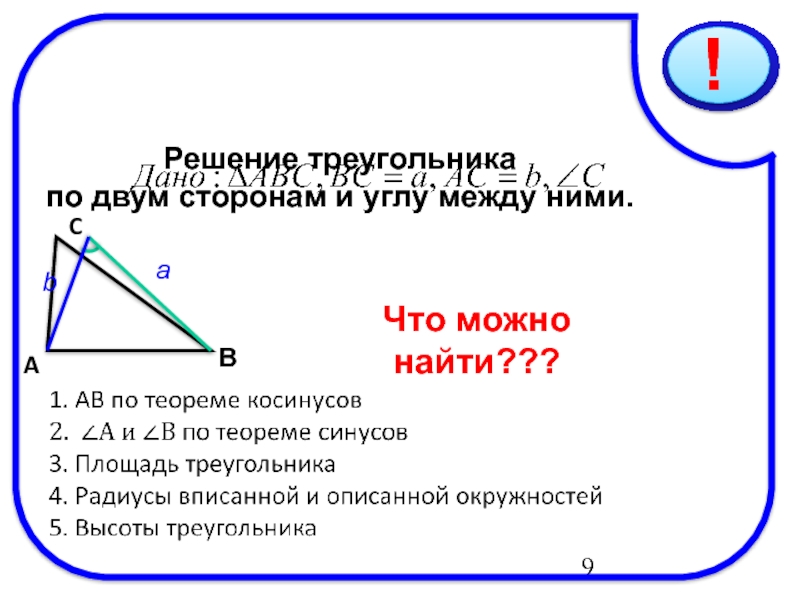
- 9. 10/03/2019 Решение треугольника по
- 10. 10/03/2019 Решение
- 11. 10/03/2019 Решаем задачу 1 С В
- 12. 10/03/2019 Решение треугольника
- 13. 10/03/2019 Решение: γ = 180º -
- 14. 10/03/2019 С В
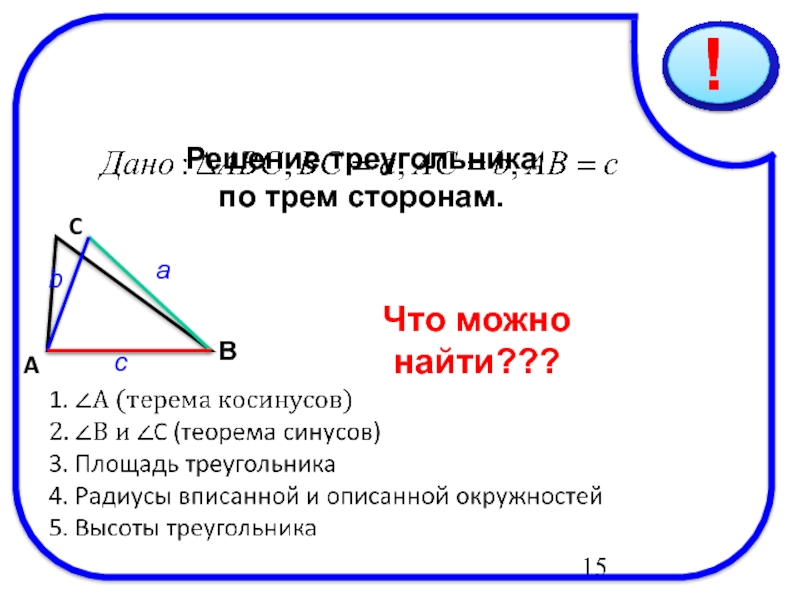
- 15. 10/03/2019 Решение треугольника по трем
- 16. 10/03/2019 Решение Пусть а – наибольшая сторона треугольника, Задача имеет одно решение
- 17. 10/03/2019
- 18. 10/03/2019 IV тип задач по двум сторонам
- 19. 10/03/2019 Решение 1. Если в намного
- 20. 10/03/2019 3. Если 0 < sinβ <
- 21. 10/03/2019 Таблица – памятка А
- 22. 10/03/2019 Ответ к примеру 1 ∠А=63º ∠B=63º c≈5,7 см
- 23. 10/03/2019 Ответ к примеру 2 ∠C=80º a≈12,3 см b≈9,1 см
- 24. 10/03/2019 Ответ к примеру 3 ∠А=54º52´ ∠B=84º16´ ∠C=40º52´
- 25. 10/03/2019 Найди ошибку
Слайд 210/03/2019
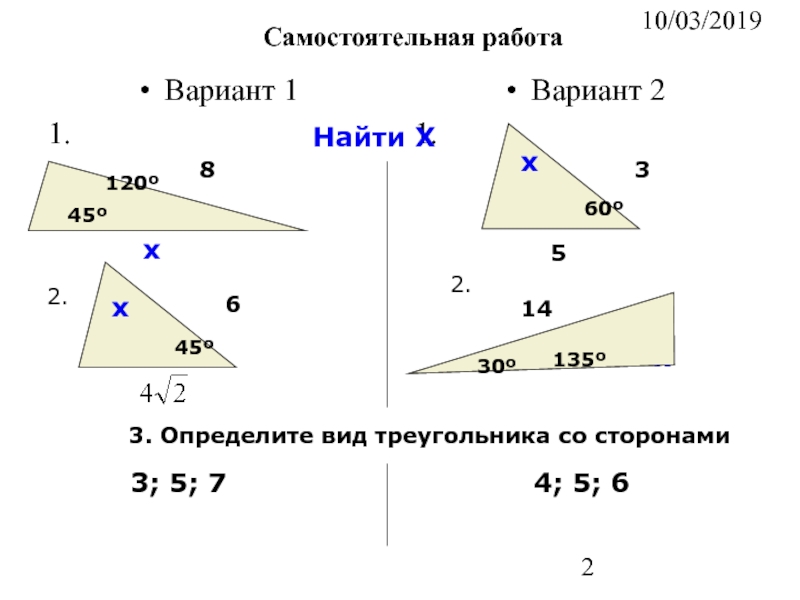
Вариант 1
1.
Вариант 2
1.
45º
120º
х
8
60º
3
х
5
2.
х
х
45º
6
135º
30º
14
2.
3. Определите вид треугольника со сторонами
3; 5; 7
4; 5; 6
Найти Х
Слайд 310/03/2019
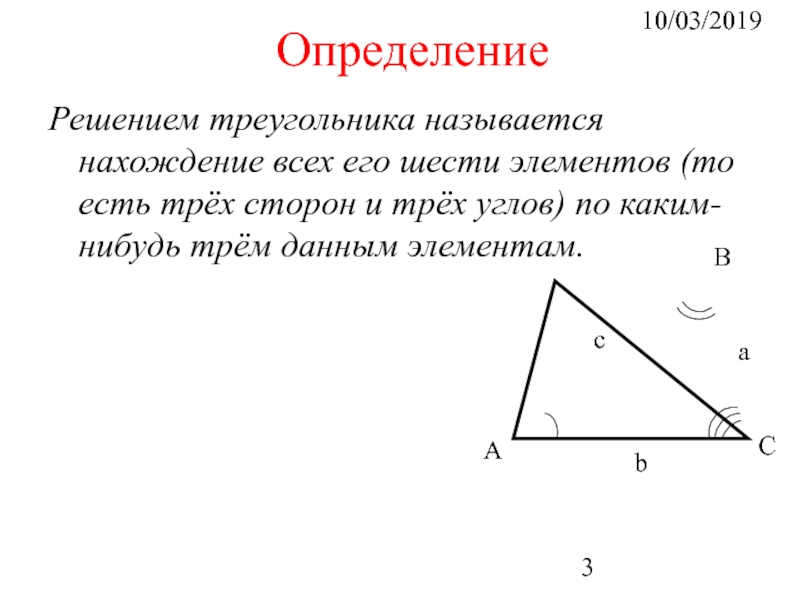
Определение
Решением треугольника называется нахождение всех его шести элементов (то есть трёх
А
В
С
c
b
a
Слайд 410/03/2019
Для этого вспомним
Решение данных задач основано на использовании теорем синусов и
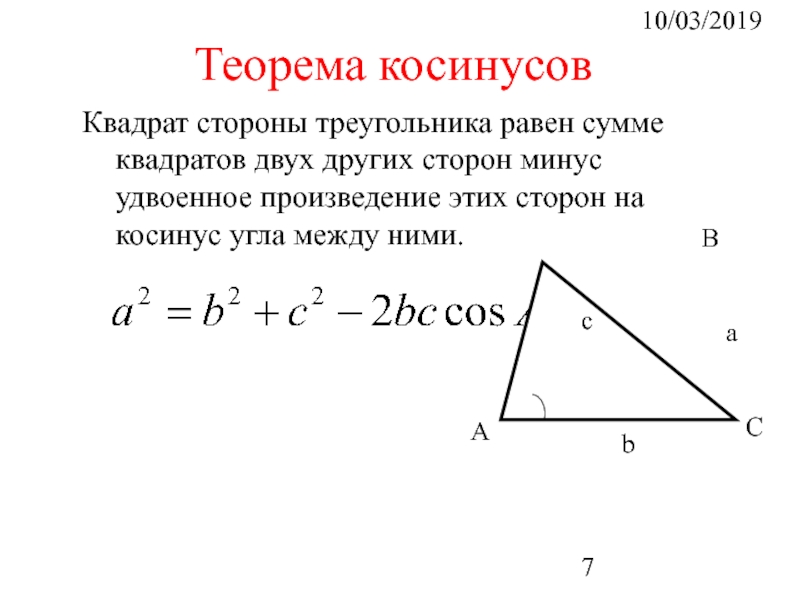
Причем, при вычислении углов треугольника предпочтительнее использовать теорему косинусов, а не теорему синусов.
Слайд 710/03/2019
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное
Теорема косинусов
А
В
С
c
b
a
Слайд 1010/03/2019
Решение
2) Если γ- тупой угол, значит α и β острые углы
и находим меньший угол (он точно острый)
Допустим это α
3) β =180º- (α + β)
Задача имеет одно решение
Слайд 1110/03/2019
Решаем задачу 1
С
В
А
Решить треугольник АВС, если a=6,3 см, b=6,3 см, ∠C=54º.
Дано:
b=6,3 см, ∠C=54º.
Найти: ∠А, ∠ В, c.
Ответ
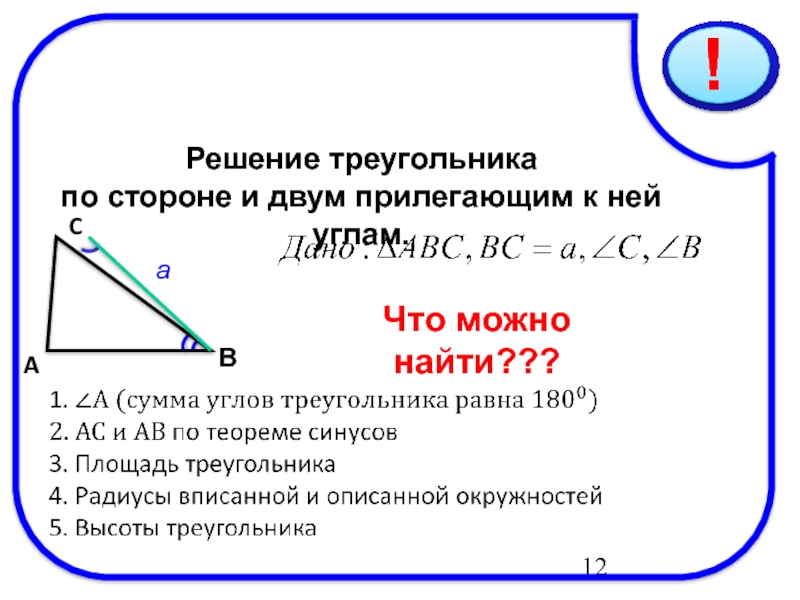
Слайд 1210/03/2019
Решение треугольника
по стороне и двум прилегающим к ней углам.
C
В
A
a
Что можно
Слайд 1410/03/2019
С
В
А
Решаем задачу 2
Решить треугольник АВС, если ∠А=60º ∠В=40º, с =14см.
Дано: ΔАВС,
∠В=40º, с=14см.
Найти: a, b, ∠С.
Ответ
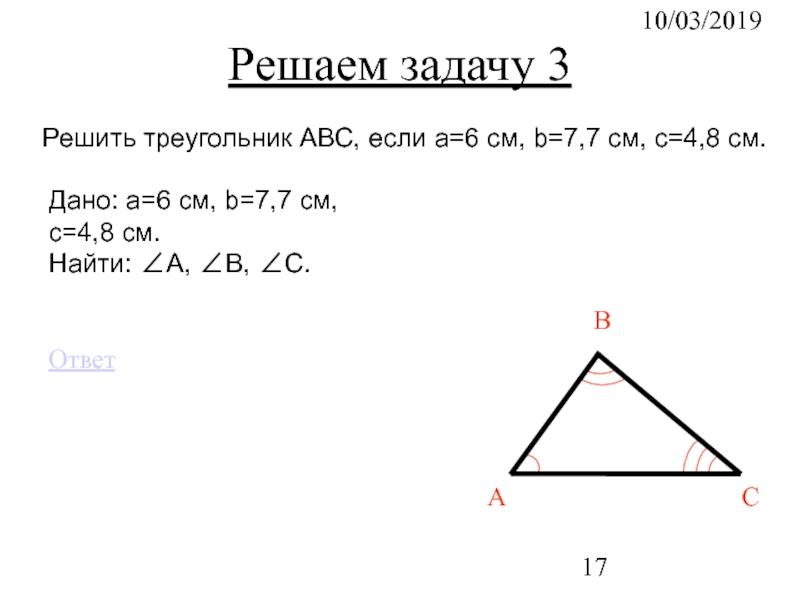
Слайд 1710/03/2019
Дано: a=6 см, b=7,7 см,
c=4,8 см.
Найти: ∠А, ∠B, ∠C.
Ответ
Решаем задачу
Решить треугольник АВС, если a=6 см, b=7,7 см, c=4,8 см.
C
А
В
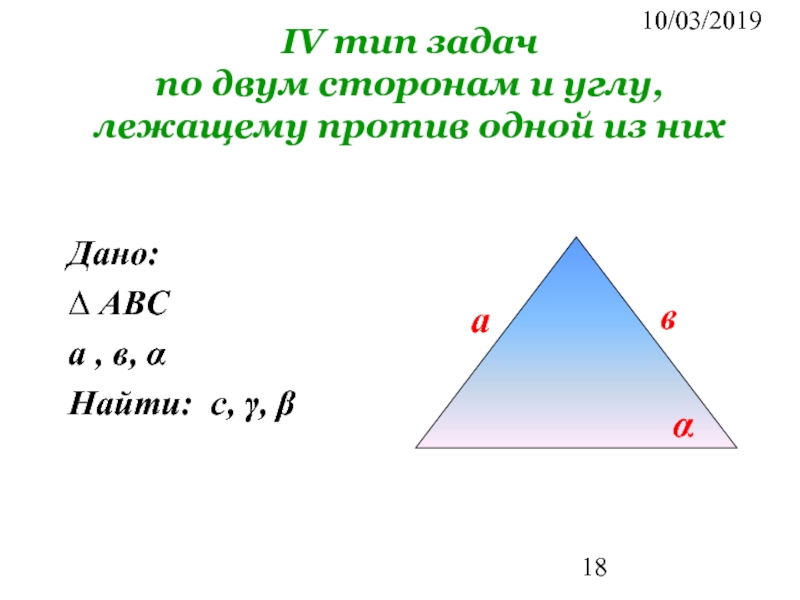
Слайд 1810/03/2019
IV тип задач
по двум сторонам и углу, лежащему против одной из
Дано:
∆ АВС
а , в, α
Найти: с, γ, β
а
в
α
Слайд 1910/03/2019
Решение
1. Если в намного больше а, то sinβ >1 и
2. Если sinβ =1, то β =90º, γ =90º-α,
с = в cosα
в этом случае задача имеет
единственное решение
Слайд 2010/03/2019
3. Если 0 < sinβ < 1 , то β может
Сравниваем а и в
Если а < в, то
существуют два угла β
-острый, значит треугольник- остроугольный
=180º- (α + )-тупой,
значит треугольник-
тупоугольный
В этом случае задача имеет два решения