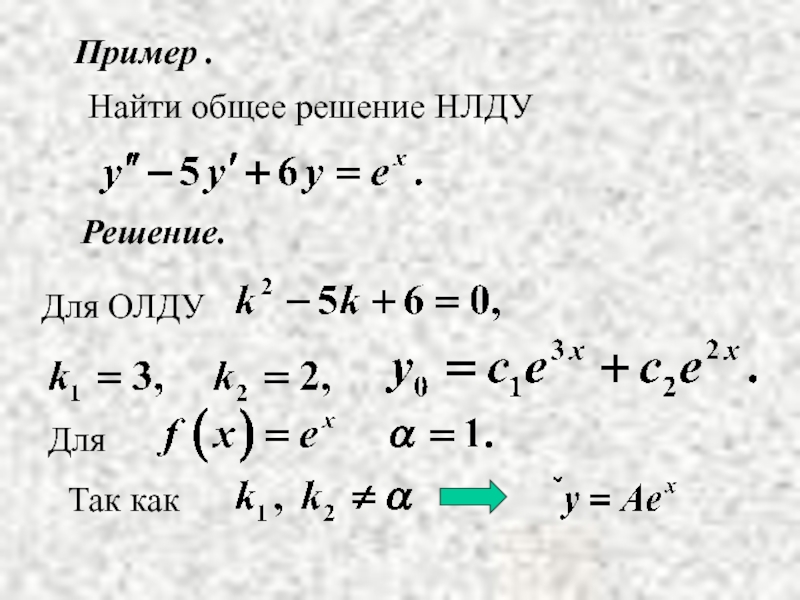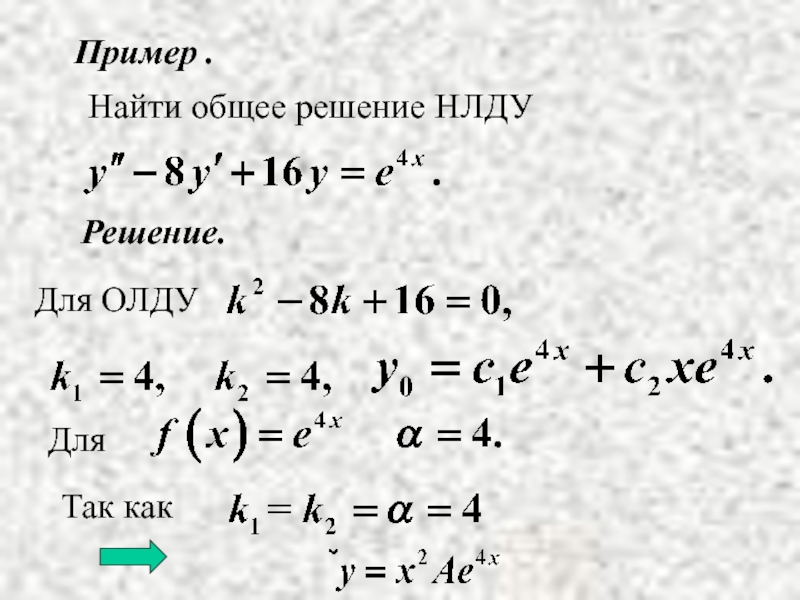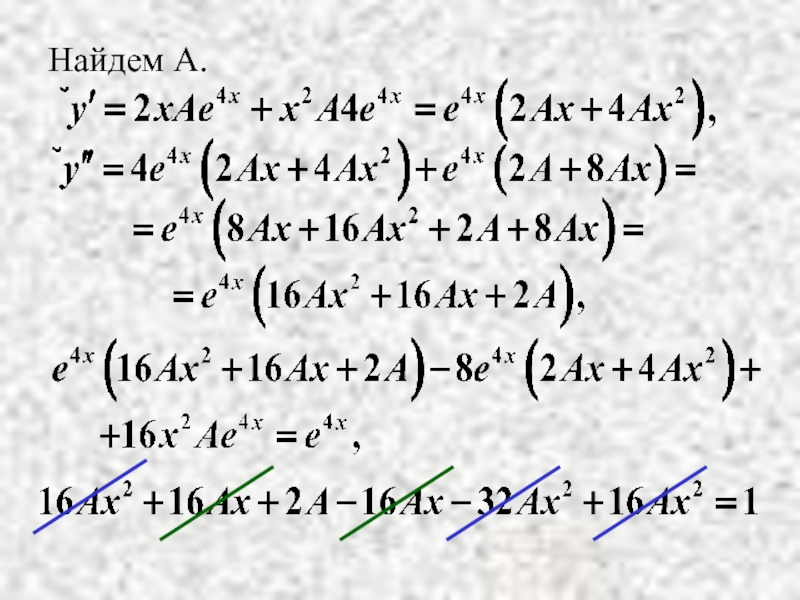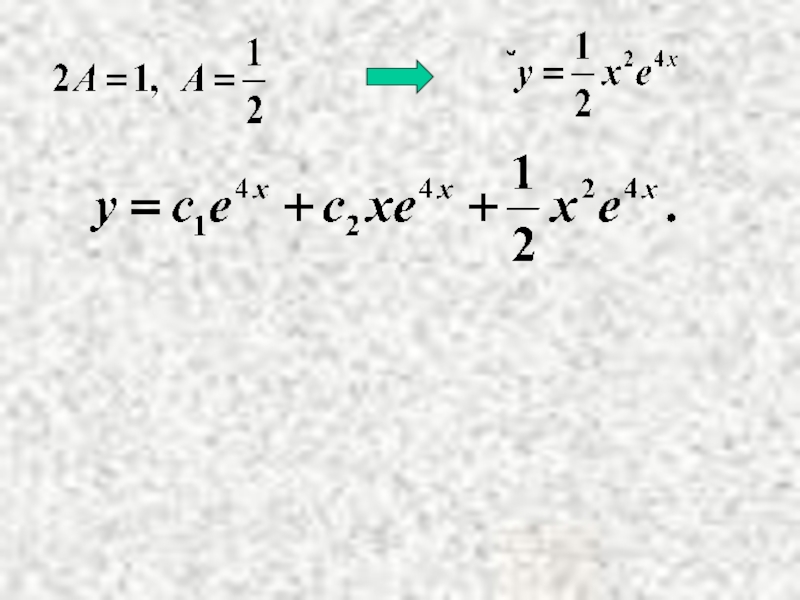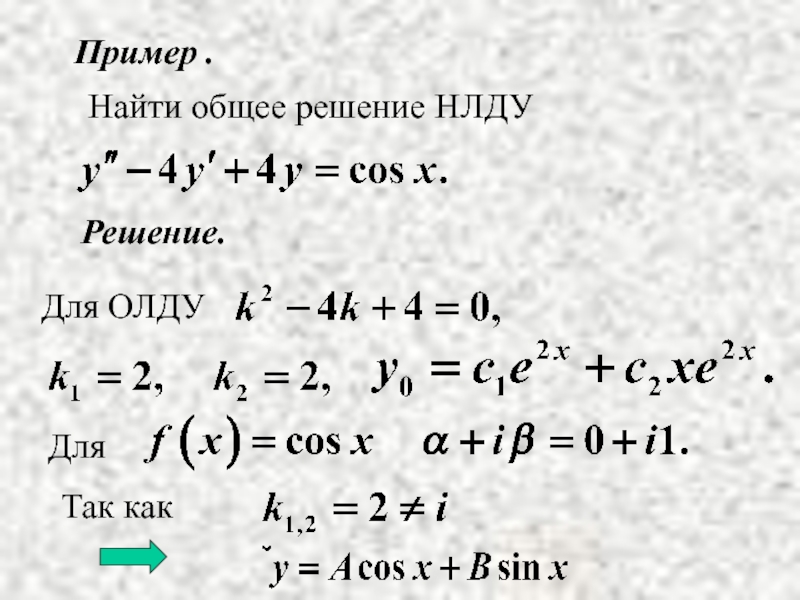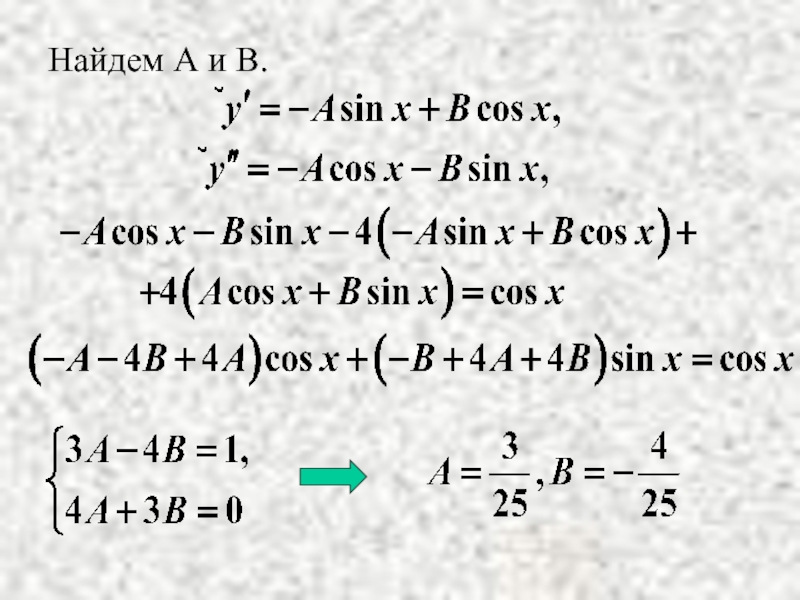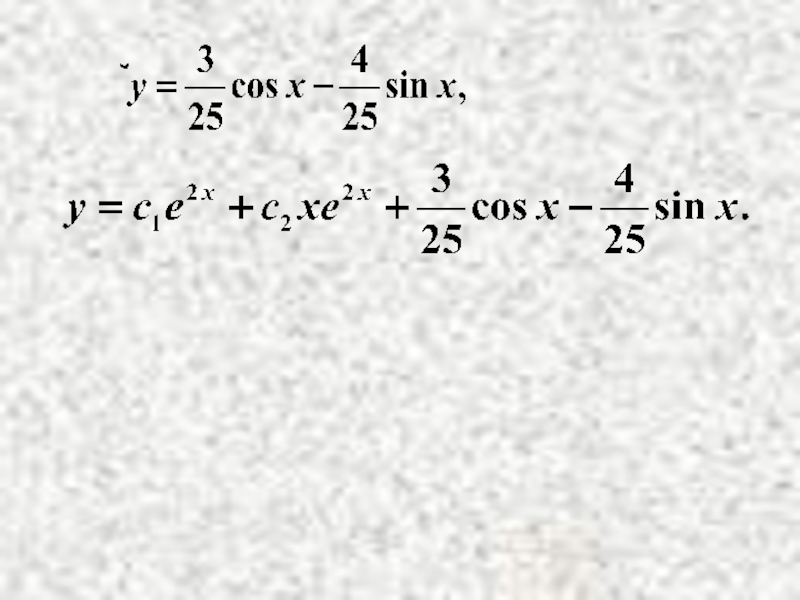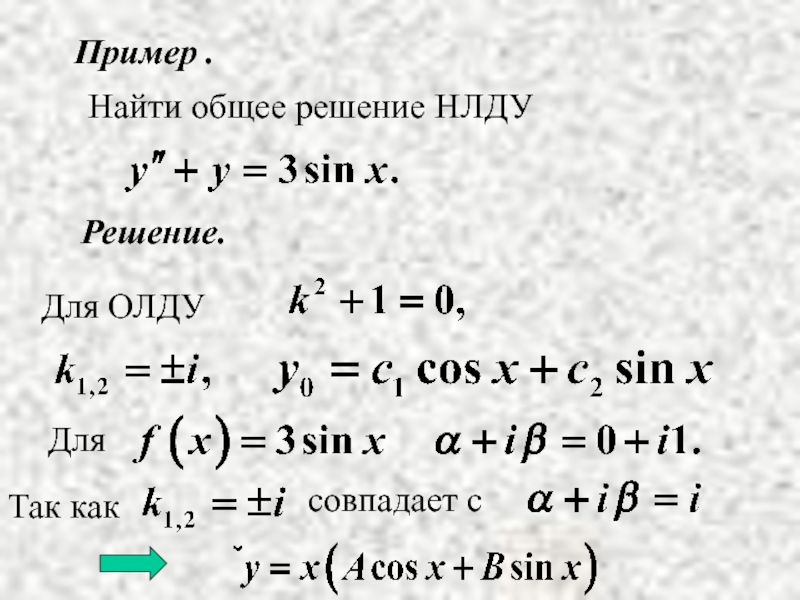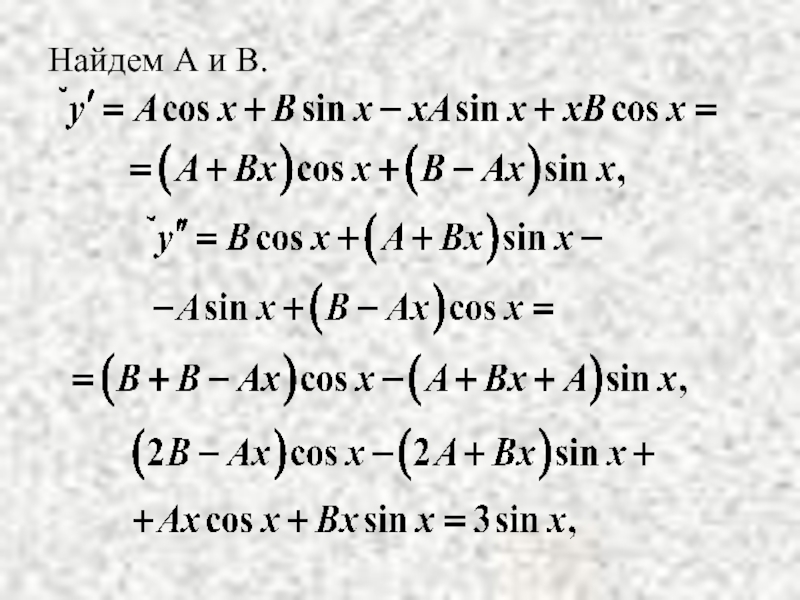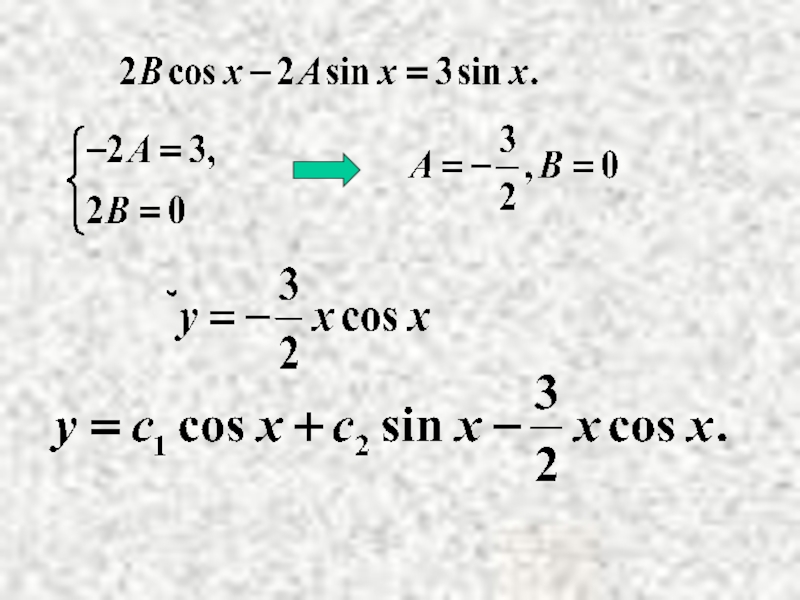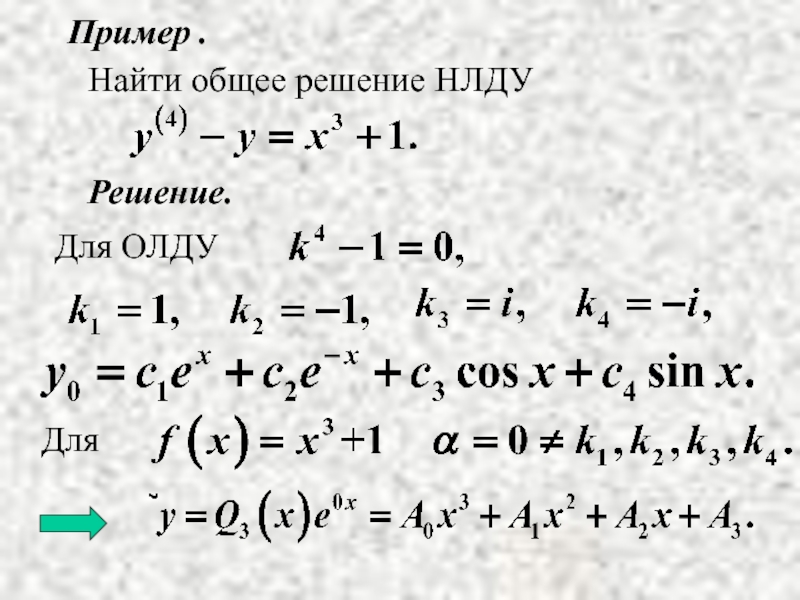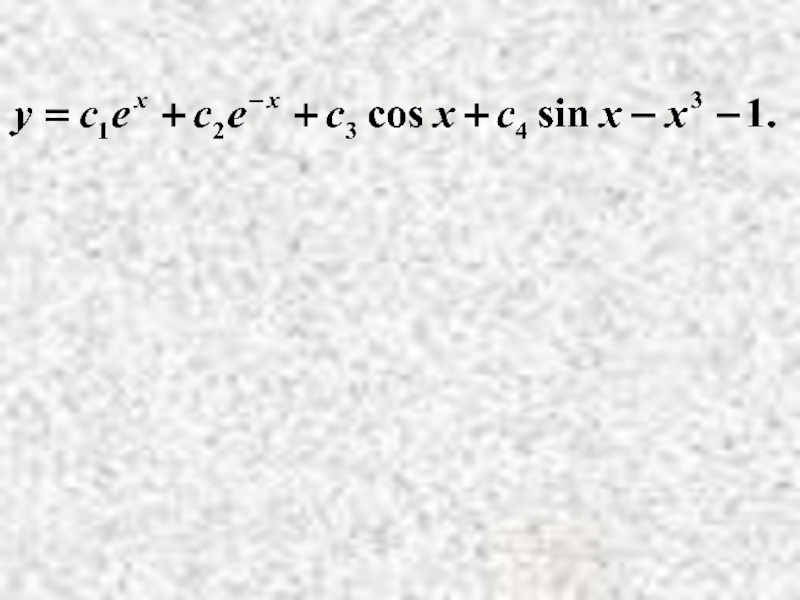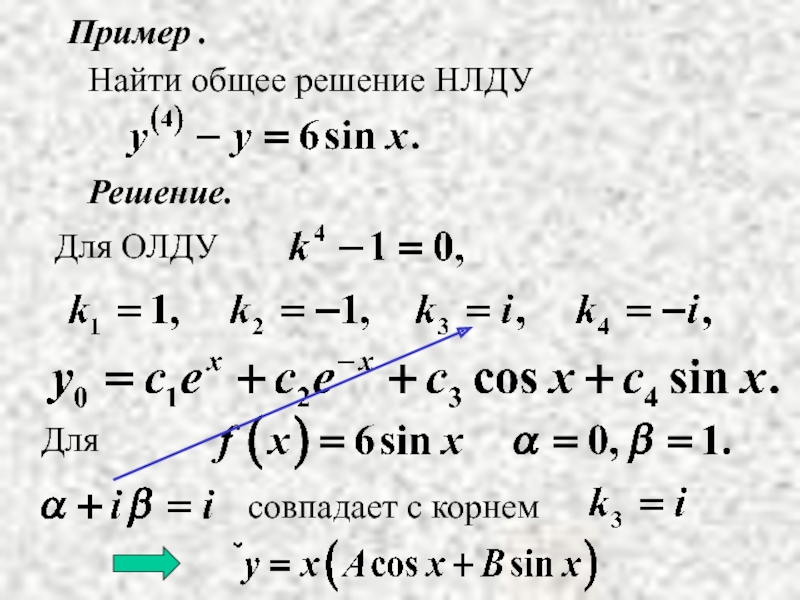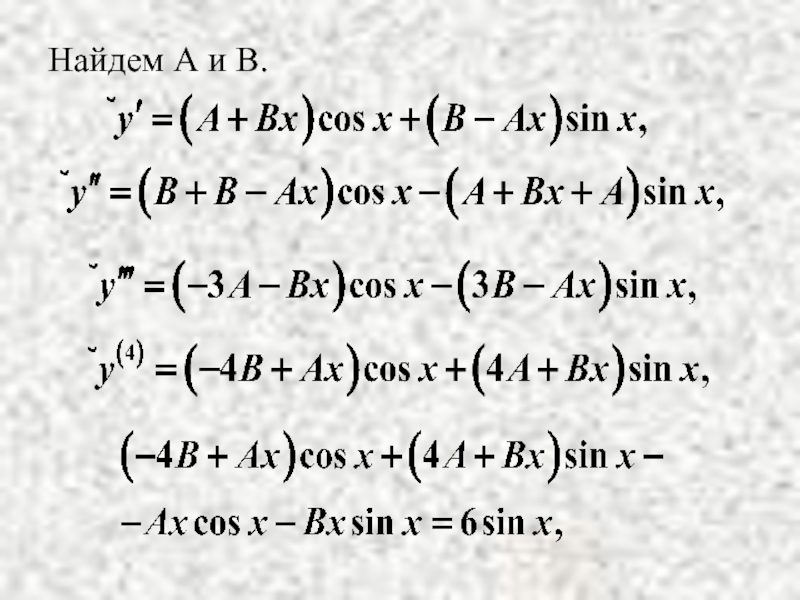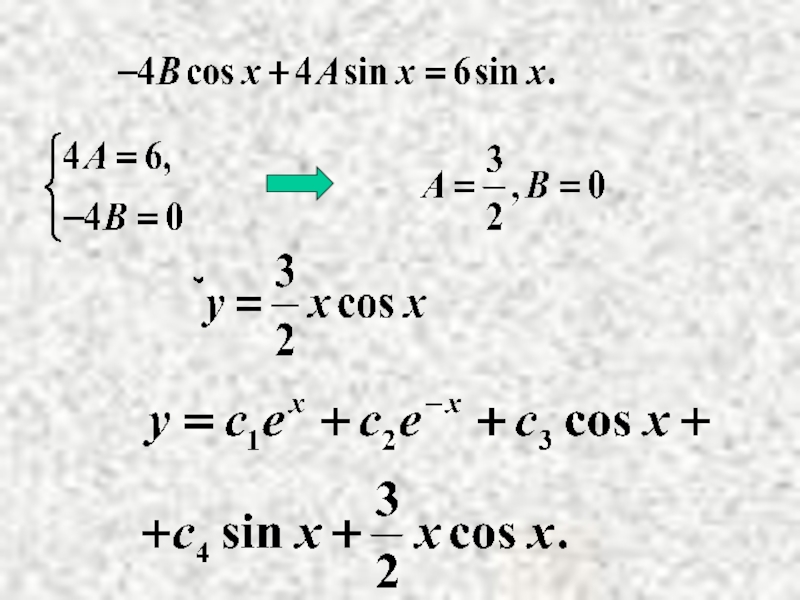- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение НЛДУ второго порядка с постоянными коэффициентами методом неопределённых коэффициентов презентация
Содержание
- 1. Решение НЛДУ второго порядка с постоянными коэффициентами методом неопределённых коэффициентов
- 3. Возможны следующие случаи:
- 5. Пример . Решение. Найти общее решение НЛДУ
- 6. Найдем А. Подставим в уравнение: Общее решение НЛДУ:
- 8. Чтобы получить тождество многочленов,
- 9. Пример . Решение. Найти общее решение НЛДУ
- 10. Найдем А.
- 12. Возможны следующие случаи:
- 13. Замечание.
- 14. Пример . Решение. Найти общее решение НЛДУ
- 15. Найдем А и В.
- 17. Пример . Решение. Найти общее решение НЛДУ
- 18. Найдем А и В.
- 20. тогда частное решение НЛДУ равно сумме этих двух решений
- 21. непрерывные функции или постоянные. Пусть общее решение соответствующего однородного уравнения
- 22. Частное решение НЛДУ ищется в виде: функции, определяемые из системы уравнений
- 23. возможны следующие случаи: Метод неопределенных коэффициентов
- 25. Пример . Решение. Найти общее решение НЛДУ
- 28. Возможны следующие случаи:
- 30. Пример . Решение. Найти общее решение НЛДУ
- 31. Найдем А и В.
- 34. Определение. Если p1 =
- 35. Решением системы (2) на (a,b) называется совокупность
- 36. ДУ n-го порядка всегда можно свести
- 37. Пример.
- 38. Задача Коши для нормальной системы
- 39. Пример решения системы ДУ методом исключения неизвестных.
Слайд 21непрерывные функции или постоянные.
Пусть общее решение соответствующего однородного уравнения
Слайд 34Определение.
Если p1 = p2 = … = pn =
1, то система (1)
называется нормальной. Она имеет следующий вид
(2)
называется нормальной. Она имеет следующий вид
(2)
Слайд 35 Решением системы (2) на (a,b) называется совокупность функций
y1 = у1(х),
у2 = у2(х), … , уn = уn(х),
непрерывно дифференцируемых на (a,b) и обращающих каждое уравнение системы (2) в верное равенство.
Общее решение системы (2) – совокупность функций y(x, c1, c2, … cn), зависящих от n произвольных постоянных интегрирования и обращающих систему (2) в систему верных равенств.
непрерывно дифференцируемых на (a,b) и обращающих каждое уравнение системы (2) в верное равенство.
Общее решение системы (2) – совокупность функций y(x, c1, c2, … cn), зависящих от n произвольных постоянных интегрирования и обращающих систему (2) в систему верных равенств.
Слайд 36 ДУ n-го порядка всегда можно свести к нормальной системе.
Систему ДУ, записанную в каноническом виде всегда можно свести к нормальному виду.
Обратно: система ДУ, как правило, но не всегда, сводится к ДУ n-го порядка, решая которое можно найти решение системы.
Обратно: система ДУ, как правило, но не всегда, сводится к ДУ n-го порядка, решая которое можно найти решение системы.
Утверждение
Слайд 37
Пример.
–
каноническая система четвертого
порядка.
Обозначим:
y1' = у3, у2' = у4.
Тогда
– нормальная система четвертого порядка.
порядка.
Обозначим:
y1' = у3, у2' = у4.
Тогда
– нормальная система четвертого порядка.
Слайд 38Задача Коши для нормальной системы
Даны система ДУ (2)
и начальные условия y1(x0) = y10,..., yn(x0) = yn0.
Найти решение системы y1(x), y2(x), … ,yn(x).
Решение.
1.
2. c1, c2, … cn из НУ
Найти решение системы y1(x), y2(x), … ,yn(x).
Решение.
1.
2. c1, c2, … cn из НУ
Слайд 39 Пример решения системы ДУ методом исключения неизвестных.
Решение.
из второго уравнения: y = z'
y' = z"
z" – z = 0
λ² – 1 = 0 ⇒ λ1,2 = ±1
Ответ. z = с1·e x + с2·e -x ,
y = с1·e x - с2·e -x
y' = z"
z" – z = 0
λ² – 1 = 0 ⇒ λ1,2 = ±1
Ответ. z = с1·e x + с2·e -x ,
y = с1·e x - с2·e -x