- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение нелинейных уравнений презентация
Содержание
- 1. Решение нелинейных уравнений
- 2. Постановка задачи Пусть требуется решить уравнение
- 3. Локализация и отделение корня Локализация корней -
- 4. Локализация и отделение корня Теорема 1. Если
- 5. Локализация и отделение корня
- 6. Локализация и отделение корня
- 7. Схема изучения метода Ограничения Алгоритм Рисунок Правило остановки Скорость сходимости Достоинства и недостатки метода
- 8. Метод половинного деления Ограничения Нет Алгоритм Строим
- 9. Метод половинного деления
- 10. Метод половинного деления Правило остановки Процесс деления
- 11. Метод половинного деления Достоинства метода Метод
- 12. Метод половинного деления
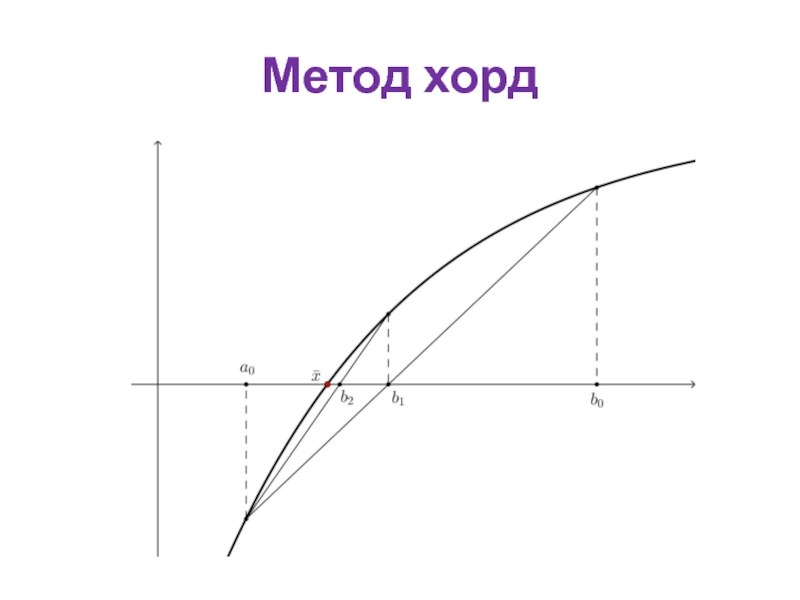
- 13. Метод хорд Ограничения. Этот метод может быть
- 14. Метод хорд
- 15. Метод хорд Алгоритм.
- 16. Метод хорд
- 17. Метод хорд При выборе нулевого приближения следует руководствоваться рисунком или следующим правилом:
- 18. Метод хорд Правило остановки Если
- 19. Метод хорд Скорость сходимости Можно рассчитывать на
- 20. Метод хорд Достоинства метода При определенных
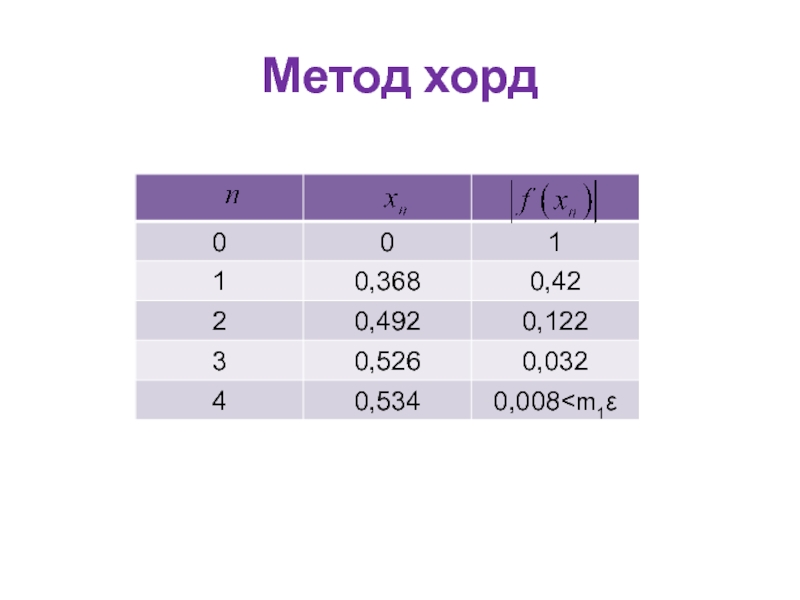
- 21. Метод хорд
- 22. Метод хорд
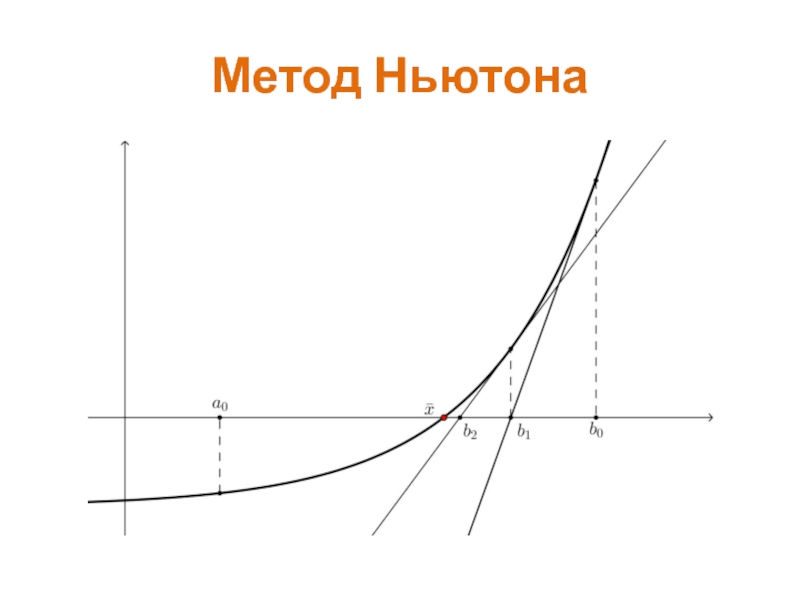
- 23. Метод Ньютона Ограничения. Те же что и
- 24. Метод Ньютона
- 25. Метод Ньютона Правило остановки То же что
- 26. Метод Ньютона Достоинства метода Высокая скорость
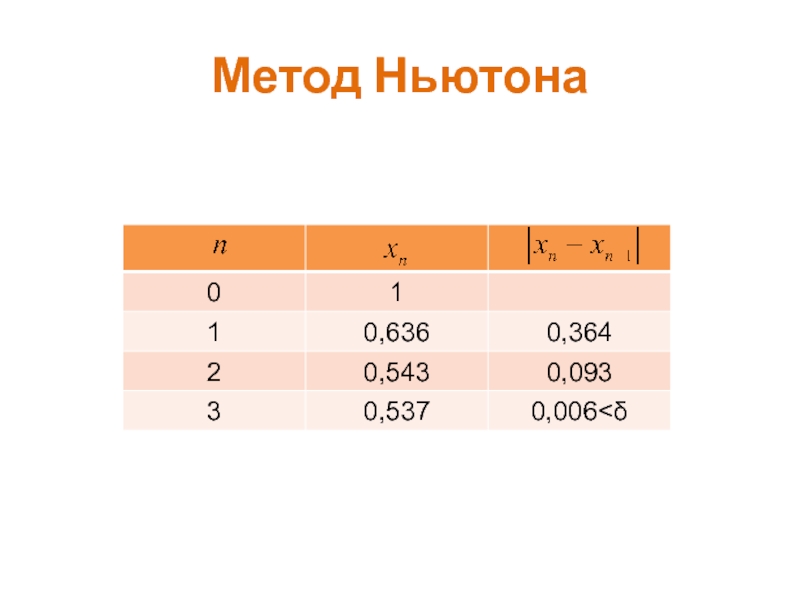
- 27. Метод Ньютона
- 28. Метод Ньютона
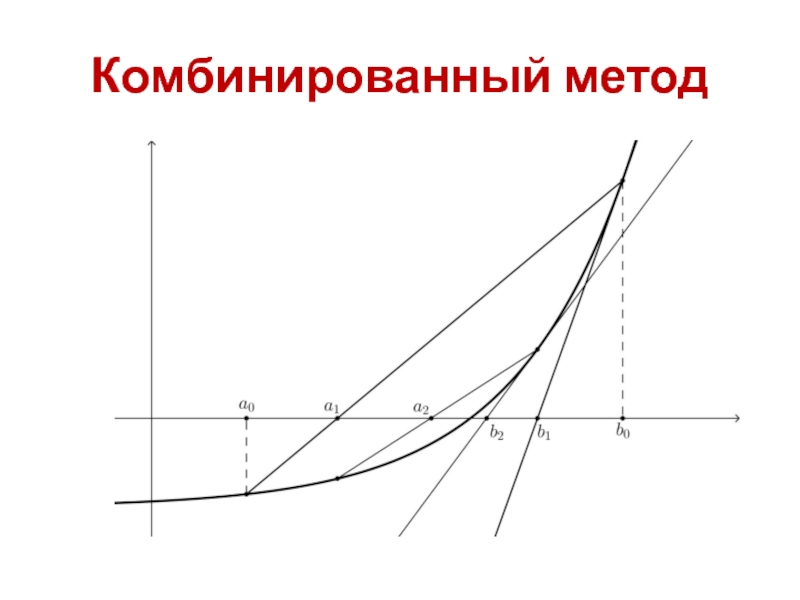
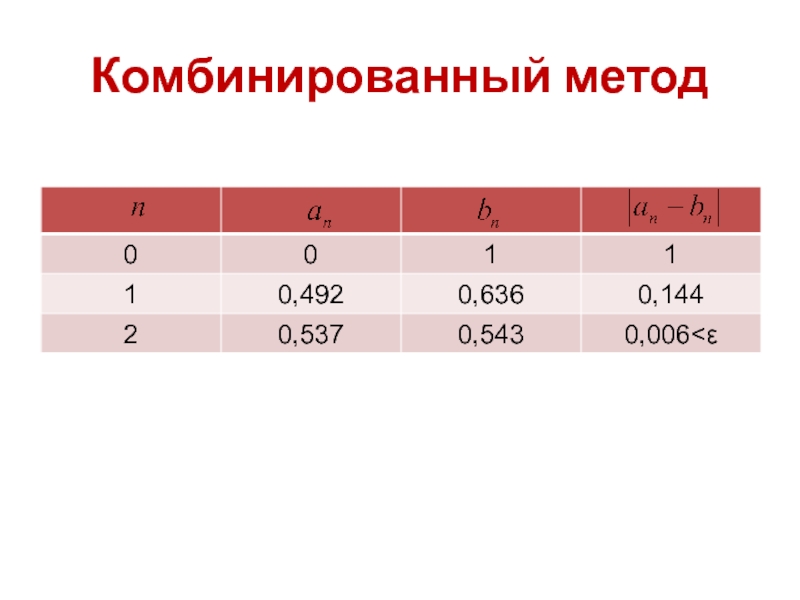
- 29. Комбинированный метод Поскольку методы касательных и хорд
- 30. Комбинированный метод В этом случае можно использовать
- 31. Комбинированный метод
- 32. Комбинированный метод
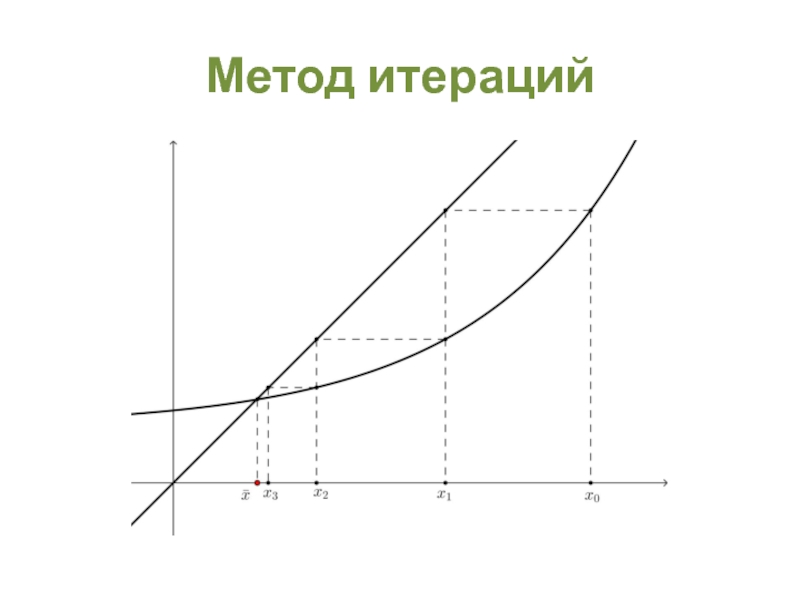
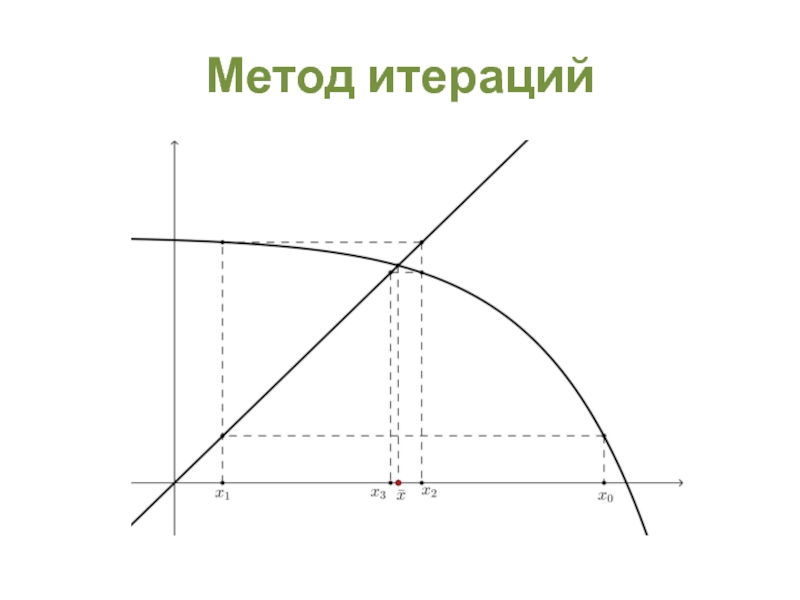
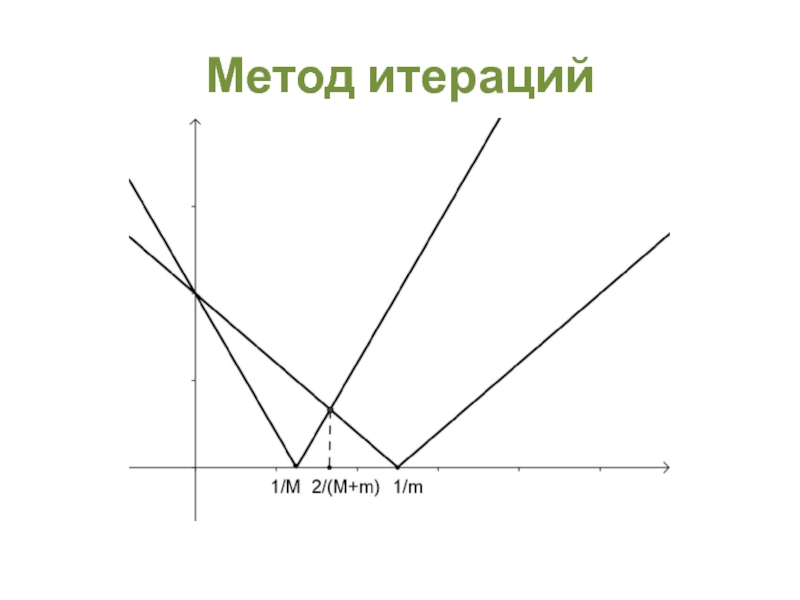
- 33. Метод итераций Ограничения. Метод итераций применяется при
- 34. Метод итераций Теорема 5. Если
- 35. Метод итераций Алгоритм Любое Далее
- 36. Метод итераций
- 37. Метод итераций
- 38. Метод итераций Правило остановки Скорость сходимости Определяется значением
- 39. Метод итераций Достоинства метода Не накапливается
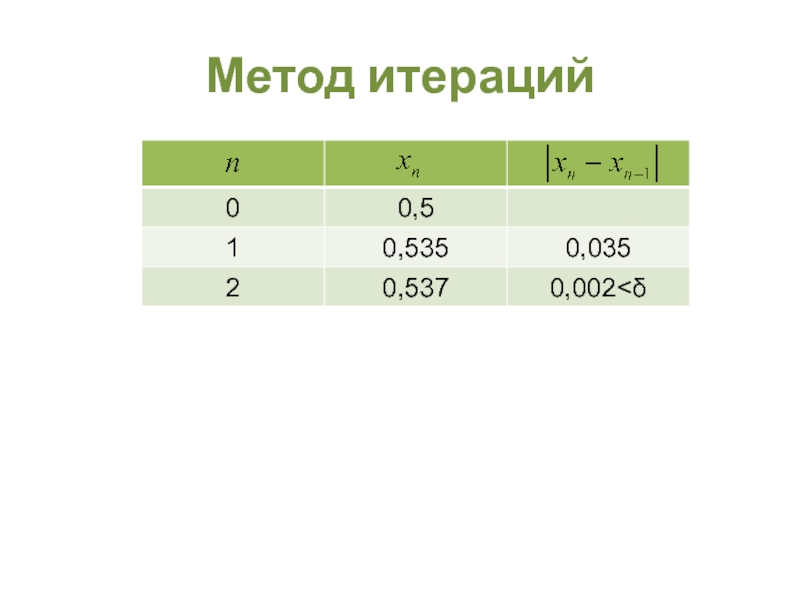
- 40. Метод итераций Теорема 7. Пусть дана непрерывно
- 41. Метод итераций
- 42. Метод итераций Воспользуемся предложенным приемом
- 43. Метод итераций
Постановка задачи Пусть требуется решить уравнение Приближенно решить уравнение или вычислить корень с точностью - это значит найти число , такое что
Слайд 2Постановка задачи
Пусть требуется решить уравнение
Приближенно решить уравнение или вычислить корень
с точностью - это значит найти число , такое что
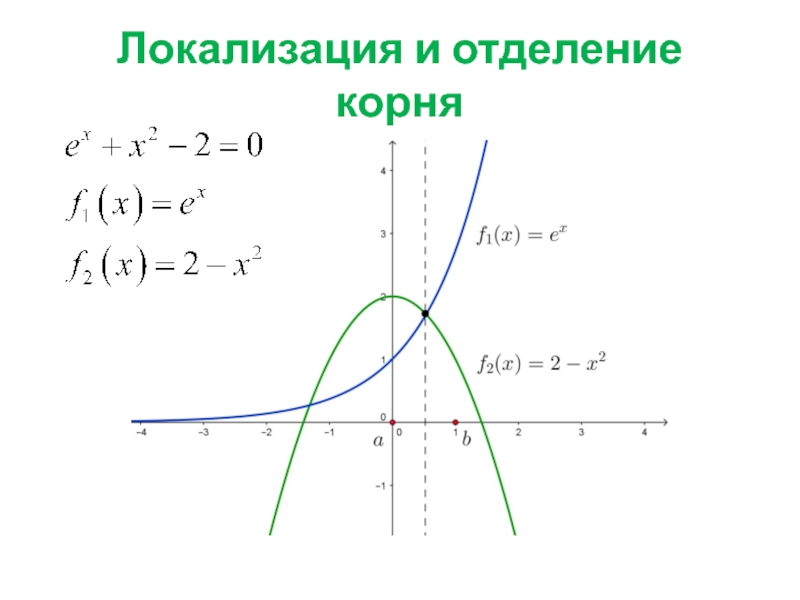
Слайд 3Локализация и отделение корня
Локализация корней - необходимо определить количество, характер и
расположение корней на числовой прямой
Отделение корня - нужно указать отрезок , внутри которого лежит один и только один корень данного уравнения
Отделение корня - нужно указать отрезок , внутри которого лежит один и только один корень данного уравнения
Слайд 4Локализация и отделение корня
Теорема 1. Если функция непрерывна на отрезке и
на его концах принимает значения разного знака, то на этом отрезке существует хотя бы одна точка, в которой функция обращается в ноль.
Теорема 2. Для того чтобы дифференцируемая на интервале функция возрастала (убывала), необходимо и достаточно, чтобы во всех его точках производная была неотрицательной (неположительной)
Теорема 2. Для того чтобы дифференцируемая на интервале функция возрастала (убывала), необходимо и достаточно, чтобы во всех его точках производная была неотрицательной (неположительной)
Слайд 6Локализация и отделение корня
непрерывная
значит корень существует
на
значит функция монотонная, это обеспечивает единственность корня
значит корень существует
на
значит функция монотонная, это обеспечивает единственность корня
Слайд 7Схема изучения метода
Ограничения
Алгоритм
Рисунок
Правило остановки
Скорость сходимости
Достоинства и недостатки метода
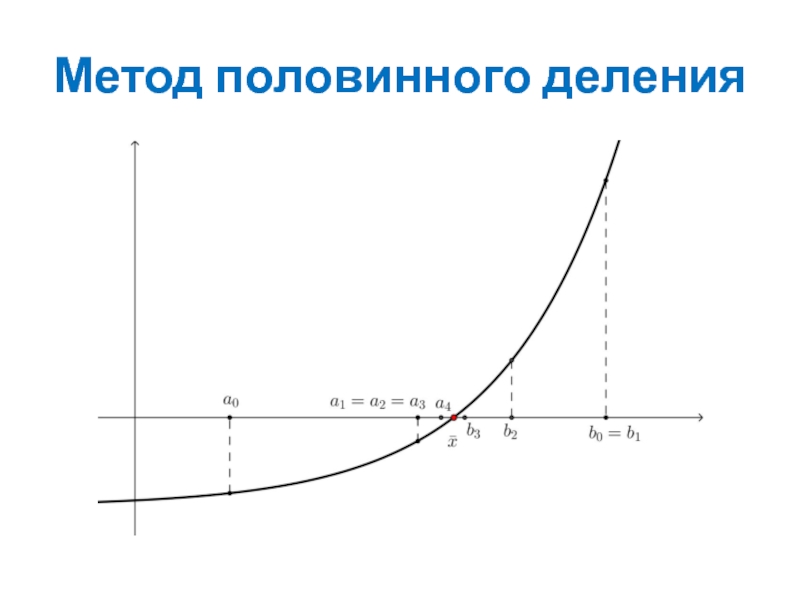
Слайд 8Метод половинного деления
Ограничения Нет
Алгоритм Строим последовательность вложенных отрезков содержащих корень
, где
Теорема 3. Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем отрезкам этой последовательности
Теорема 3. Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем отрезкам этой последовательности
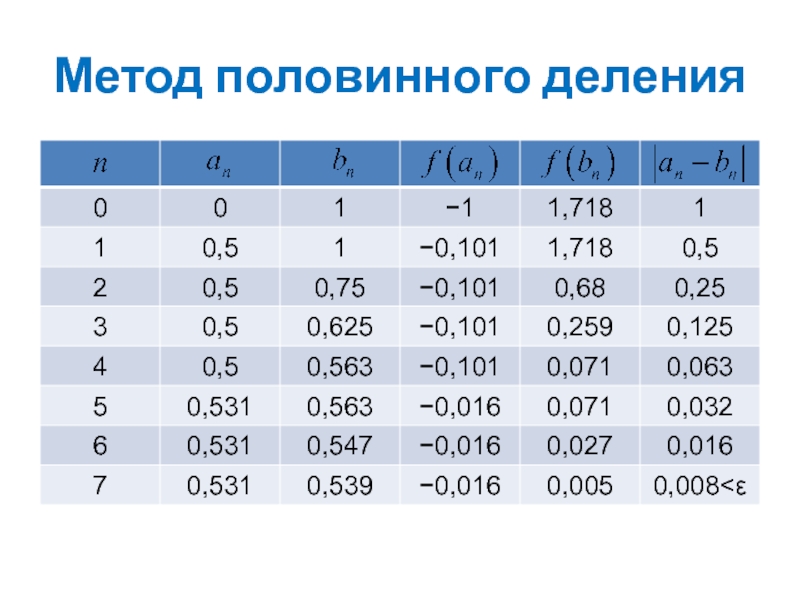
Слайд 10Метод половинного деления
Правило остановки Процесс деления продолжается до тех пор, пока
длина отрезка не станем меньше
Скорость сходимости
Метод сходится со скоростью геометрической прогрессии со знаменателем
Это довольно медленно
Скорость сходимости
Метод сходится со скоростью геометрической прогрессии со знаменателем
Это довольно медленно
Слайд 11Метод половинного деления
Достоинства метода
Метод очень прост
Не имеет ограничений
Легко программируется
Недостатки
метода
Если есть проблемы с отделением корня и в отрезке их несколько, то не понятно к какому сходимся последовательность
Метод не применим к корням четной кратности
Не обобщается на системы уравнений
Если есть проблемы с отделением корня и в отрезке их несколько, то не понятно к какому сходимся последовательность
Метод не применим к корням четной кратности
Не обобщается на системы уравнений
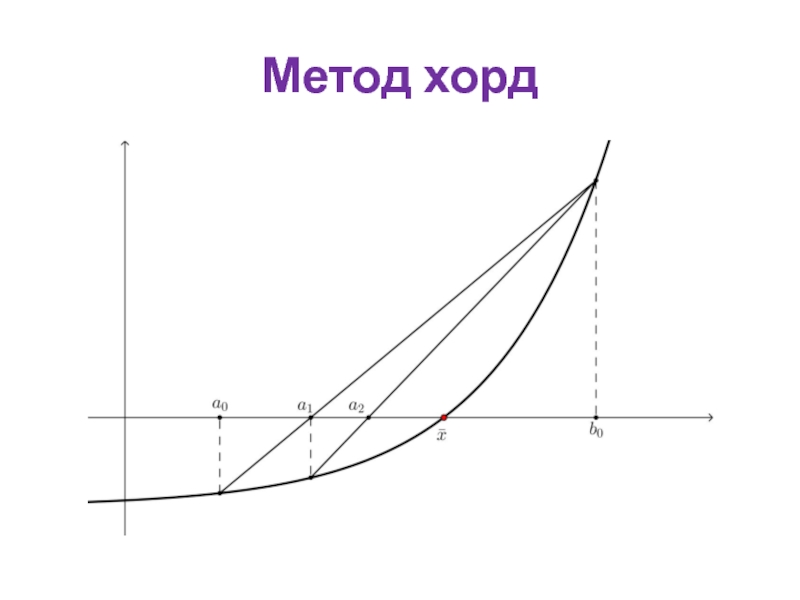
Слайд 13Метод хорд
Ограничения. Этот метод может быть использован только в том случае,
если функция на отрезке не имеет точек перегиба, т.е. постоянна по знаку вторая производная
Алгоритм.
,
если
Алгоритм.
,
если
Слайд 15Метод хорд
Алгоритм.
,
если
Теорема 4. Если функция непрерывна и выпукла на отрезке, то уравнение имеет на отрезке единственный корень, и последовательность монотонно сходится к нему.
если
Теорема 4. Если функция непрерывна и выпукла на отрезке, то уравнение имеет на отрезке единственный корень, и последовательность монотонно сходится к нему.
Слайд 17Метод хорд
При выборе нулевого приближения следует руководствоваться рисунком или следующим правилом:
Слайд 18Метод хорд
Правило остановки
Если
,
то вычисления можно прекратить, когда выполнено условие
В силу выпуклости функции можно утверждать, что
то вычисления можно прекратить, когда выполнено условие
В силу выпуклости функции можно утверждать, что
Слайд 19Метод хорд
Скорость сходимости
Можно рассчитывать на его быструю сходимости только если функция
близка к линейной
Если на функцию не накладывать ограничений, то метод может проигрывать даже методу половинного деления
Если на функцию не накладывать ограничений, то метод может проигрывать даже методу половинного деления
Слайд 20Метод хорд
Достоинства метода
При определенных ограничениях имеет неплохую скорость сходимости
Недостатки метода
Ограничения
на свойства функции
Сходимость к корню с одной стороны
Усложненное правило остановки
Сходимость к корню с одной стороны
Усложненное правило остановки
Слайд 25Метод Ньютона
Правило остановки То же что и для метода хорд
Скорость сходимости.
При выборе начального приближения из достаточно малой окрестности корня метод сходится квадратично, т.е. скорость сходимости велика. Для кратного корня скорость геометрической прогрессии
Слайд 26Метод Ньютона
Достоинства метода
Высокая скорость сходимости
Недостатки метода
Ограничения на свойства функции
Сходимость к
корню с одной стороны
Усложненное правило остановки
Усложненное правило остановки
Слайд 29Комбинированный метод
Поскольку методы касательных и хорд дают приближения один с избытком,
а другой с недостатком их часто используют совместно - комбинированный метод. В этом случае получаем систему вложенных отрезков
содержащих корень уравнения.
содержащих корень уравнения.
Слайд 30Комбинированный метод
В этом случае можно использовать правило остановки, как в методе
половинного деления
При этом использование метода Ньютона позволяет повысить скорость сходимости метода хорд
При этом использование метода Ньютона позволяет повысить скорость сходимости метода хорд
Слайд 33Метод итераций
Ограничения. Метод итераций применяется при решении уравнений вида:
Функция
определенная на отрезке
называется сжимающей, если существует такая положительная постоянная , что для любых выполняется неравенство
называется сжимающей, если существует такая положительная постоянная , что для любых выполняется неравенство
Слайд 34Метод итераций
Теорема 5. Если дифференцируема на
отрезке,
причем , то она является сжимающей на этом отрезке, и можно взять
Теорема 6. Пусть функция является сжимающей на отрезке и переводит этот отрезок в себя, при всех
. Тогда уравнение на этом отрезке имеет, и притом, единственное решение.
причем , то она является сжимающей на этом отрезке, и можно взять
Теорема 6. Пусть функция является сжимающей на отрезке и переводит этот отрезок в себя, при всех
. Тогда уравнение на этом отрезке имеет, и притом, единственное решение.
Слайд 39Метод итераций
Достоинства метода
Не накапливается ошибка вычислений. Ухудшение очередного приближения отразится
лишь на числе итераций
При небольшом значении высокая скорость сходимости
Недостатки метода
Подбор сжимающей функции с небольшим значением
Усложненное правило остановки
При небольшом значении высокая скорость сходимости
Недостатки метода
Подбор сжимающей функции с небольшим значением
Усложненное правило остановки
Слайд 40Метод итераций
Теорема 7. Пусть дана непрерывно дифференцируема на отрезке функция, причем
,
тогда для любого , функция
является сжимающей на отрезке,
причем при коэффициент сжатия
принимает минимально возможное значение
тогда для любого , функция
является сжимающей на отрезке,
причем при коэффициент сжатия
принимает минимально возможное значение
