- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реляционная алгебра презентация
Содержание
- 1. Реляционная алгебра
- 2. Содержание Необходимые определения Операции реляционной алгебры Объединение
- 3. Необходимые определения Отношение – это двумерная
- 4. Операции реляционной алгебры Классические операции теории множеств
- 5. Объединение Объединением двух отношений R1 и R2,
- 6. Пересечение Пересечением двух отношений R1 и R2,
- 7. Разность Разностью двух отношений R1 и R2,
- 8. Произведение Сцеплением двух кортежей называется кортеж, полученный
- 9. Селекция Селекцией (выборкой) отношения по некоторому условию
- 10. Проекция Проекцией отношения на подмножество его атрибутов
- 11. Деление Делением отношения R1 на отношение R2
- 12. Соединение Соединением двух отношений по некоторому условию
- 13. Примеры 4. Выдать ФИО студентов с указанием
- 14. Примеры 5. Получить список студентов, которые в
- 15. Задание Получить названия животных, средняя продолжительность жизни
- 16. Контрольные вопросы Что такое «Отношение»? Перечислите операции
- 17. Список литературы Дьяков, И.А. Базы данных. Язык
Слайд 2Содержание
Необходимые определения
Операции реляционной алгебры
Объединение
Задание
Примеры
Пересечение
Разность
Произведение
Селекция
Проекция
Контрольные вопросы
Список литературы
Деление
Соединение
Слайд 3Необходимые определения
Отношение – это двумерная таблица, содержащая некоторые данные, для которой
В таблице не может быть одинаковых строк.
Имена столбцов должны быть различны.
Порядок строк в таблице может быть произвольным.
Все строки в таблице должны иметь одинаковую структуру.
Схема отношения – список атрибутов этого отношения.
Совместимые по объединению отношения – это отношения, имеющие одно и то же множество имен атрибутов.
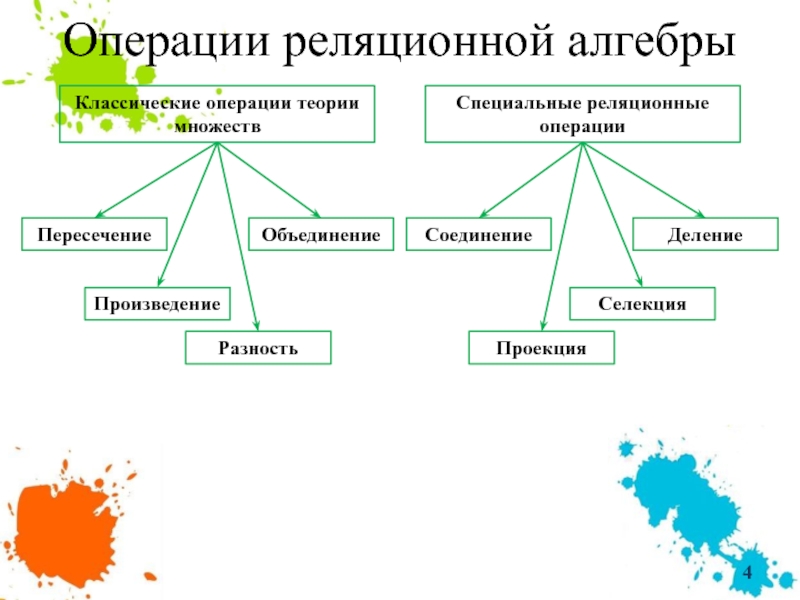
Слайд 4Операции реляционной алгебры
Классические операции теории множеств
Специальные реляционные операции
Объединение
Разность
Пересечение
Произведение
Проекция
Селекция
Деление
Соединение
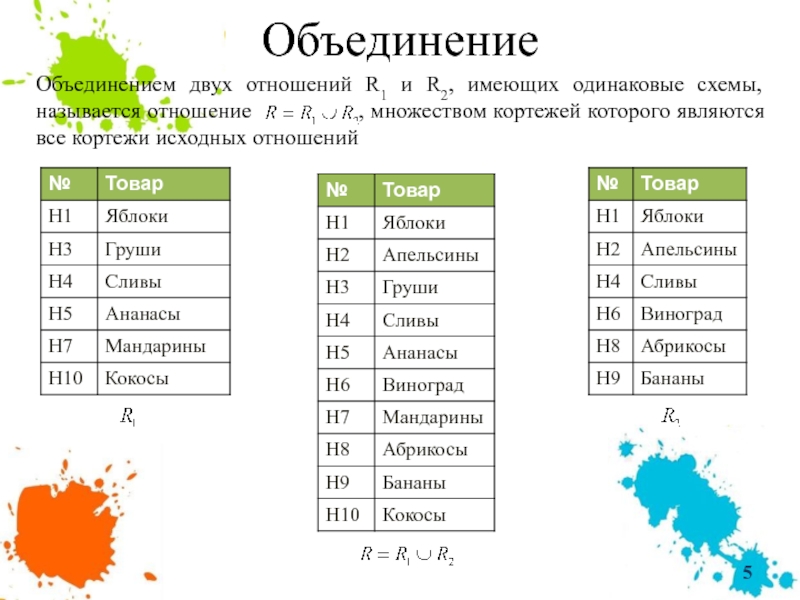
Слайд 5Объединение
Объединением двух отношений R1 и R2, имеющих одинаковые схемы, называется отношение
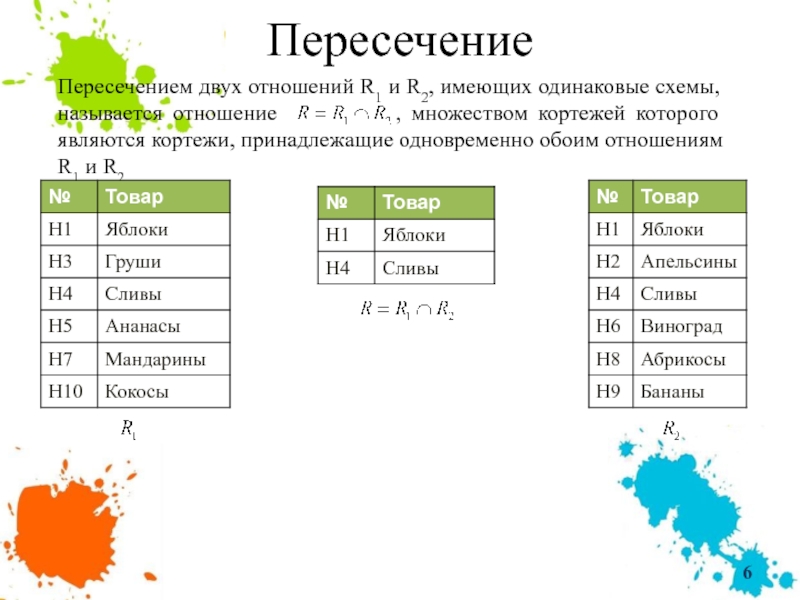
Слайд 6Пересечение
Пересечением двух отношений R1 и R2, имеющих одинаковые схемы, называется отношение
Слайд 7Разность
Разностью двух отношений R1 и R2, имеющих одинаковые схемы, называется отношение
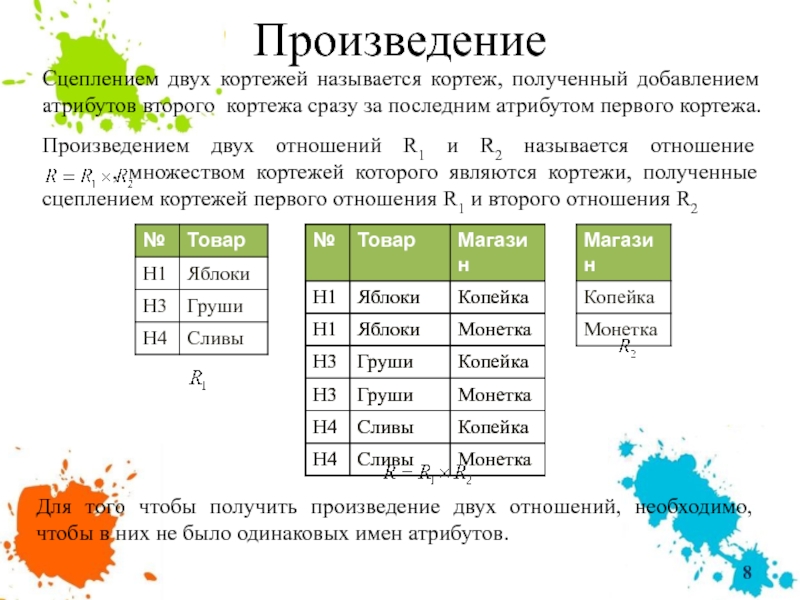
Слайд 8Произведение
Сцеплением двух кортежей называется кортеж, полученный добавлением атрибутов второго кортежа сразу
Произведением двух отношений R1 и R2 называется отношение , множеством кортежей которого являются кортежи, полученные сцеплением кортежей первого отношения R1 и второго отношения R2
Для того чтобы получить произведение двух отношений, необходимо, чтобы в них не было одинаковых имен атрибутов.
Слайд 9Селекция
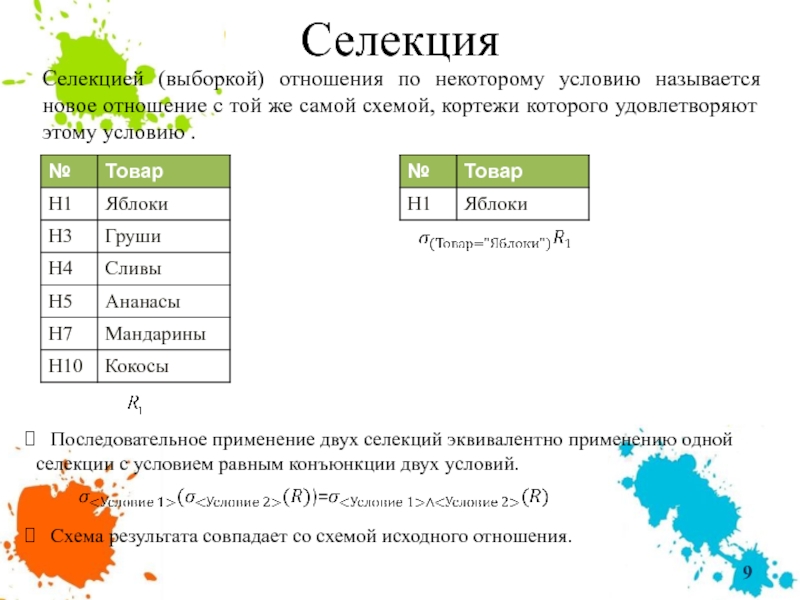
Селекцией (выборкой) отношения по некоторому условию называется новое отношение с той
Последовательное применение двух селекций эквивалентно применению одной селекции с условием равным конъюнкции двух условий.
Схема результата совпадает со схемой исходного отношения.
Слайд 10Проекция
Проекцией отношения на подмножество его атрибутов называется отношение, содержащее эти атрибуты
Слайд 11Деление
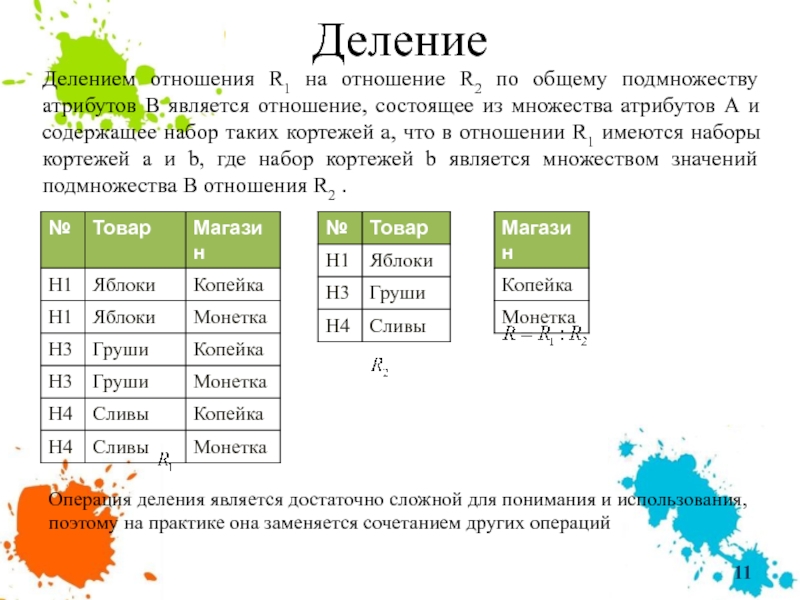
Делением отношения R1 на отношение R2 по общему подмножеству атрибутов В
Операция деления является достаточно сложной для понимания и использования, поэтому на практике она заменяется сочетанием других операций
Слайд 12Соединение
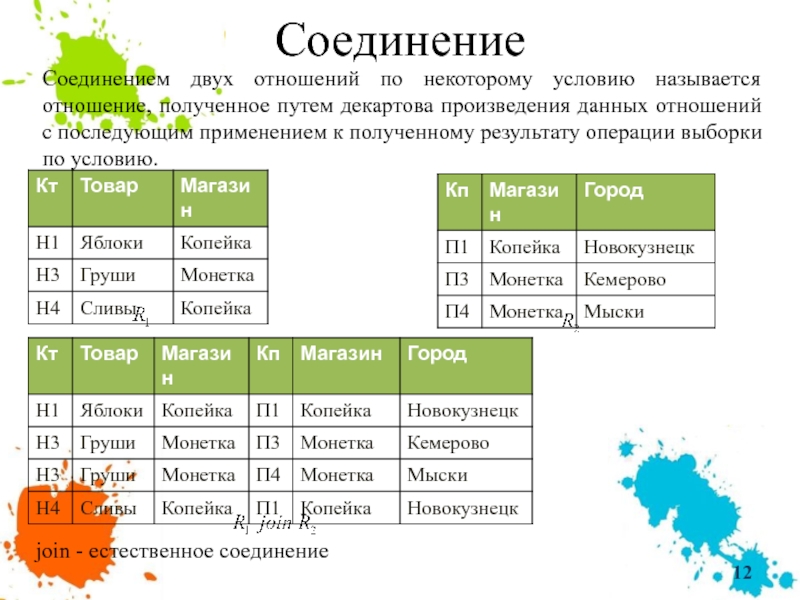
Соединением двух отношений по некоторому условию называется отношение, полученное путем декартова
join - естественное соединение
Слайд 13Примеры
4. Выдать ФИО студентов с указанием их групп.
1. Выдать ФИО студентов,
2. Выдать ФИО студентов, не получающих стипендию.
3. Сформировать список студентов – мужчин, получающих стипендию.
Слайд 14Примеры
5. Получить список студентов, которые в январе сдали на оценку «отлично»
6. Получить список студентов, которые сдали математику и физику на оценку «отлично»
7. Получить список кафедр, преподаватели которых поставили как минимум одну оценку «неудовлетворительно»
Слайд 15Задание
Получить названия животных, средняя продолжительность жизни которых меньше 15 лет.
Получить названия
Получить список животных, которые либо кенгуру, либо живут в среднем меньше 5 лет.
Получить список животных с указанием классов.
Получить список животных, обитающих в Московском зоопарке, с указанием количества экземпляров.
Получить список животных, питающихся фруктами или злаками.
Получить список продуктов, которыми кормят дельфинов в Московском зоопарке.
Получить список зоопарков, где альбатросов кормят мелкими беспозвоночными.
Слайд 16Контрольные вопросы
Что такое «Отношение»?
Перечислите операции реляционной алгебры.
Что получится в результате выполнения
Что получится в результате выполнения операции произведения? Приведите пример. Сформулируйте условие, предъявляемое к отношениям, для возможности выполнения данной операции.
Слайд 17Список литературы
Дьяков, И.А. Базы данных. Язык SQL [Электронный ресурс]: учебн. пособие
http://biblioclub.ru/index.php?page=book_view_red&book_id=277628
(5. Реляционная алгебра)
Шнырев, С.Л. Базы данных [Электронный ресурс]: учебн. пособие / С.Л. Шнырев. – Электрон. текстовые дан. – Москва: Изд-во НИЯУ МИФИ, 2011. – Режим доступа:
http://biblioclub.ru/index.php?page=book_view_red&book_id=231519
(2.2 Реляционная алгебра, реляционное исчисление)









![Список литературыДьяков, И.А. Базы данных. Язык SQL [Электронный ресурс]: учебн. пособие / И.А. Дьяков. –](/img/tmb/5/469594/04a65159ffe5d8277242d7791a89ef84-800x.jpg)





