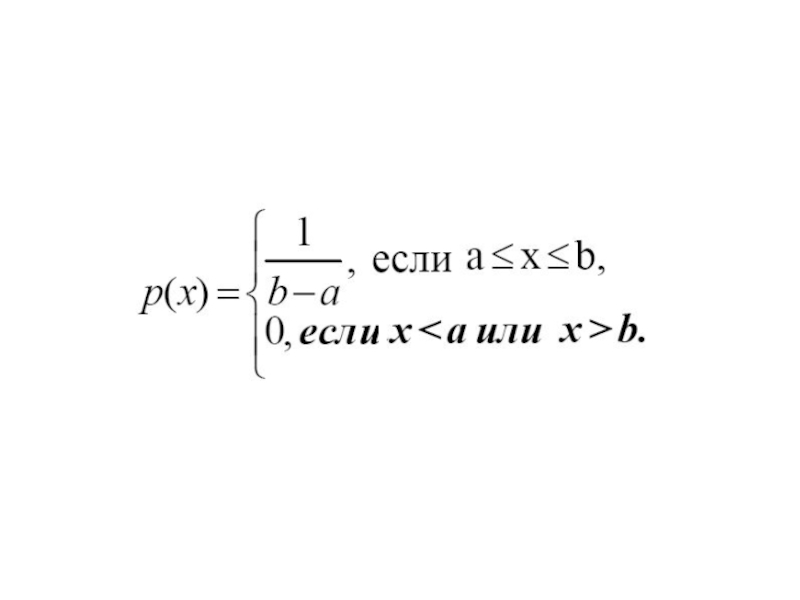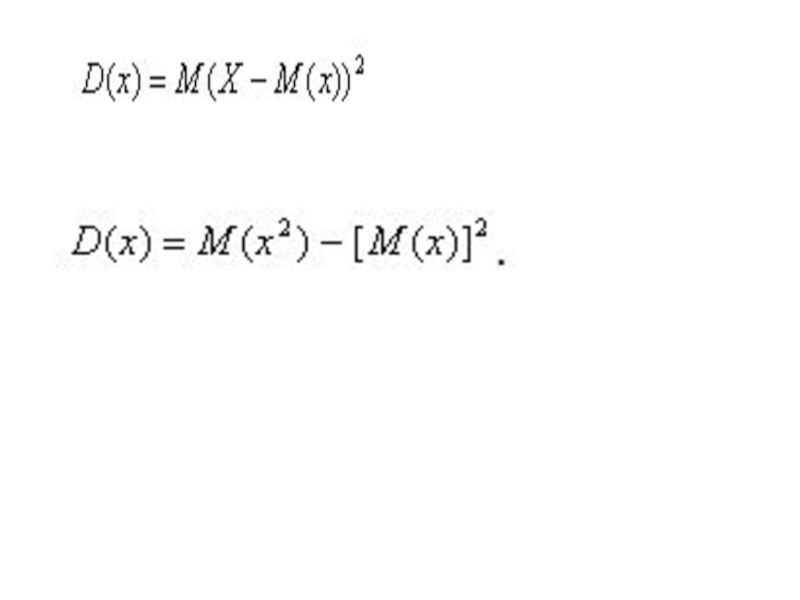- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Распределения непрерывных случайных величин презентация
Содержание
- 1. Распределения непрерывных случайных величин
- 2. Случайную величину назовем непрерывной, если ее функция
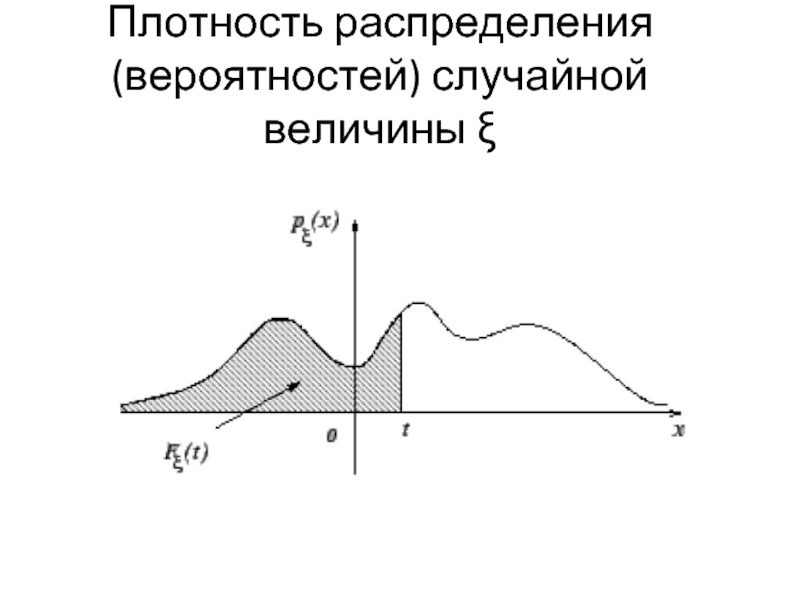
- 3. Плотность распределения (вероятностей) случайной величины ξ
- 4. Равномерное распределение Равномерно распределенная на отрезке [a,b] случайная величина имеет функцию распределения
- 5. Функция равномерного распределения имеет вид:
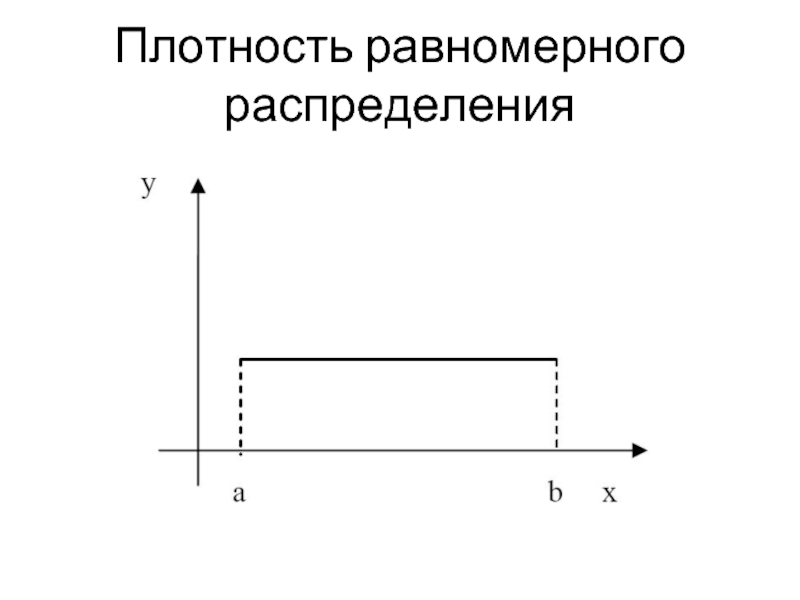
- 6. Плотность равномерного распределения
- 8. Нормальное распределение Случайная величина распределена по нормальному
- 10. Параметр m определяет положение центра нормальной
- 11. Генеральная совокупность (популяция) W – полный
- 12. Различные значения признака, наблюдающиеся у членов
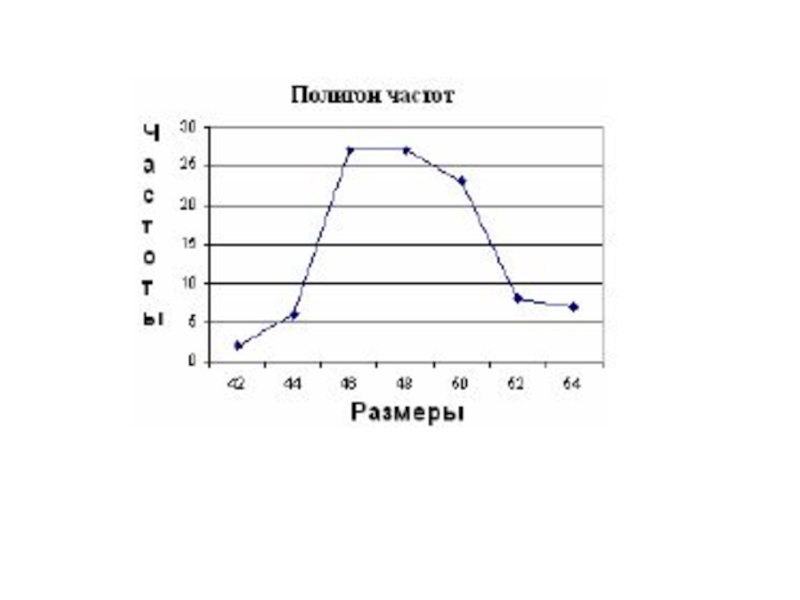
- 13. Пример 1. При регистрации размеров продаваемой магазином
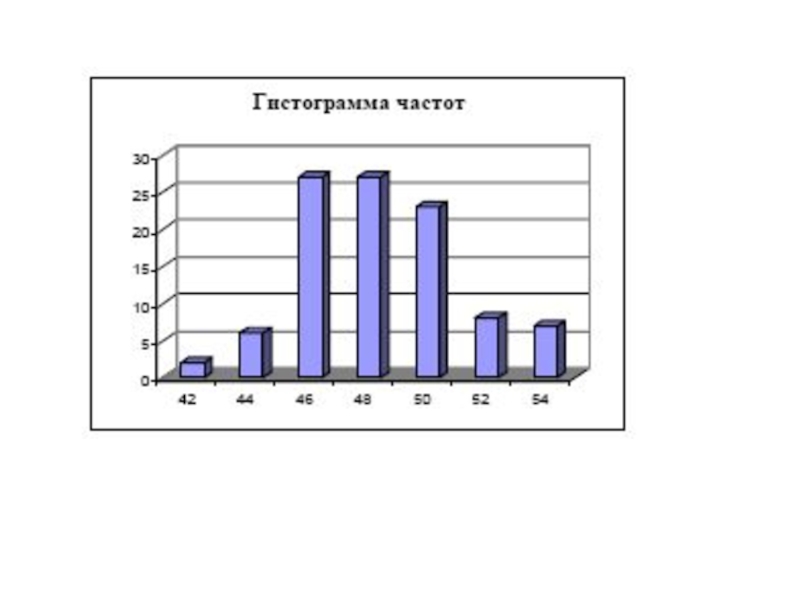
- 15. Построение признаков и частот по выборке
- 18. Формы распределения Симметричные Несимметричные Умеренно ассиметричные Крайне ассиметричные U-образные
- 19. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
- 20. Математическое ожидание и его свойства Математическим ожиданием
- 21. Для непрерывной сл. величины, заданной функцией
- 22. Свойства мат.ожидания 1. Если случайная величина ξ
- 23. Свойства мат.ожидания 2. Пусть η = аξ
- 24. Свойства мат.ожидания 3. Пусть η – случайная
- 25. Свойства мат.ожидания 4. Если ξ 1 и
- 26. Средние величины Среднее арифметическое определяется по формуле
- 27. Мода – (наиболее вероятное значение) является наиболее
- 28. Дисперсия и среднее квадратическое отклонение дают представление
- 29. Дисперсия Dξ дискретной случайной величины ξ определяется формулой
- 30. Дисперсией непрерывной случайной величины называют математическое
- 32. Свойства дисперсии
- 33. Свойства дисперсии
Случайную величину назовем непрерывной, если ее функция распределения не имеет скачков и разрывов. Непрерывной называется случайная величина ξ, функцию распределения которой F(x) можно представить в виде: Функция p(x)
Слайд 2Случайную величину назовем непрерывной, если ее функция распределения не имеет скачков
и разрывов.
Непрерывной называется случайная величина ξ, функцию распределения которой F(x) можно представить в виде:
Функция p(x) называется плотностью распределения (вероятностей) случайной величины ξ
Непрерывной называется случайная величина ξ, функцию распределения которой F(x) можно представить в виде:
Функция p(x) называется плотностью распределения (вероятностей) случайной величины ξ
Слайд 4Равномерное распределение
Равномерно распределенная на отрезке [a,b] случайная величина имеет функцию распределения
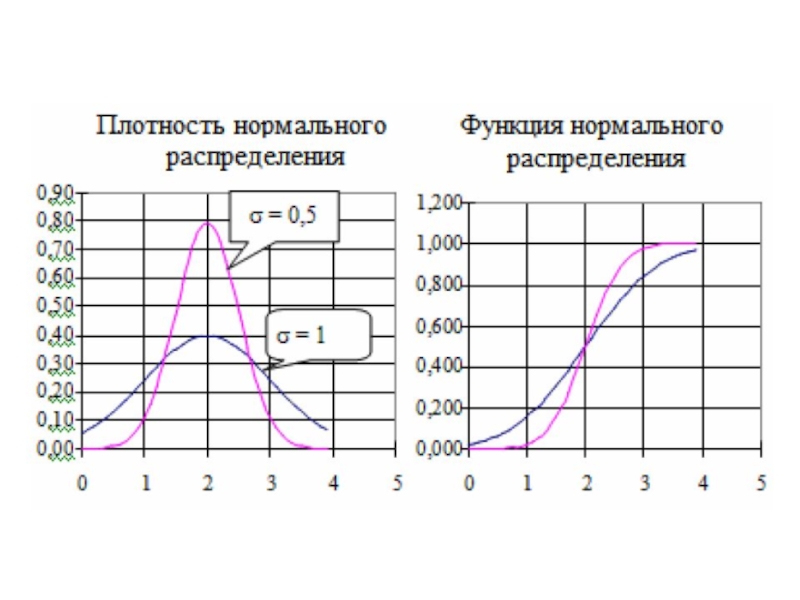
Слайд 8Нормальное распределение
Случайная величина распределена по нормальному или гауссову закону, если она
имеет плотность распределения
где m – математическое ожидание или среднее значение нормального закона;
σ- среднее квадратичное отклонение
где m – математическое ожидание или среднее значение нормального закона;
σ- среднее квадратичное отклонение
Слайд 10
Параметр m определяет положение центра нормальной плотности, а σ – разброс
относительно центра.
Если m=0, σ = 1, то такой нормальный закон называется стандартным и его функция распределения обозначается через Ф(х).
Если m=0, σ = 1, то такой нормальный закон называется стандартным и его функция распределения обозначается через Ф(х).
Слайд 11Генеральная совокупность (популяция) W
– полный набор объектов w, с которыми
связана данная проблема. С каждым объектом связана величина (или величины), называемая исследуемым признаком (xi).
Слайд 12
Различные значения признака, наблюдающиеся у членов генеральной совокупности (или выборки), называются
вариантами, а числа, показывающие сколько раз встречается каждый вариант – их частотами.
Слайд 13Пример 1.
При регистрации размеров продаваемой магазином женской верхней одежды были получены
данные о 100 покупках
Слайд 18Формы распределения
Симметричные
Несимметричные
Умеренно ассиметричные
Крайне ассиметричные
U-образные
Слайд 20Математическое ожидание и его свойства
Математическим ожиданием (или средним значением) дискретной случайной
величины называется сумма произведений всех её возможных значение на соответствующие им вероятности.
Слайд 21
Для непрерывной сл. величины, заданной функцией плотности вероятности f(x), математическое ожидание
определяется в виде интеграла
Слайд 22Свойства мат.ожидания
1. Если случайная величина ξ принимает всего одно значение С
с вероятностью единица. Математическое ожидание постоянной величины равно этой постоянной:
МС = С * 1 = С
МС = С * 1 = С
Слайд 23Свойства мат.ожидания
2. Пусть η = аξ + b – случайная величина,
выраженная линейной функцией, тогда математическое ожидание этой случайной величины равно:
М(аξ + b ) = аМξ + b
М(аξ + b ) = аМξ + b
Слайд 24Свойства мат.ожидания
3. Пусть η – случайная величина, которая является суммой двух
других величин:
η = ξ 1+ ξ 2.
Тогда математическое ожидание суммы двух случайных величин равно сумме математических ожиданий каждой из этих величин:
М(ξ 1+ ξ 2) = Мξ 1+ Мξ 2
η = ξ 1+ ξ 2.
Тогда математическое ожидание суммы двух случайных величин равно сумме математических ожиданий каждой из этих величин:
М(ξ 1+ ξ 2) = Мξ 1+ Мξ 2
Слайд 25Свойства мат.ожидания
4. Если ξ 1 и ξ 2 независимы, то математическое
ожидание их произведений η = ξ 1 ξ 2 равно произведению их математических ожиданий
М(ξ 1ξ 2) = Мξ 1*Мξ 2
М(ξ 1ξ 2) = Мξ 1*Мξ 2
Слайд 27Мода – (наиболее вероятное значение) является наиболее часто встречающейся в выборке
величиной.
Медиана – срединное значение для ряда измерений n. Для ее вычисления необходимо все наблюдения расположить в порядке возрастания или убывания результатов. Если n – нечетное число, то медиана просто является числом, находящимся в середине упорядоченной последовательности. При четном равна среднему арифметическому двух расположенных в середине значений упорядоченной последовательности.
Медиана – срединное значение для ряда измерений n. Для ее вычисления необходимо все наблюдения расположить в порядке возрастания или убывания результатов. Если n – нечетное число, то медиана просто является числом, находящимся в середине упорядоченной последовательности. При четном равна среднему арифметическому двух расположенных в середине значений упорядоченной последовательности.
Слайд 28Дисперсия и среднее квадратическое отклонение
дают представление о разбросе случайных величин относительно
их среднего значения
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
Слайд 30
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения. Если
возможные значения Х принадлежат отрезку [a,b], то
