- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Распределение параметров сложных систем презентация
Содержание
- 1. Распределение параметров сложных систем
- 2. Принцип 80/20 20% ассортимента продукции - 80%
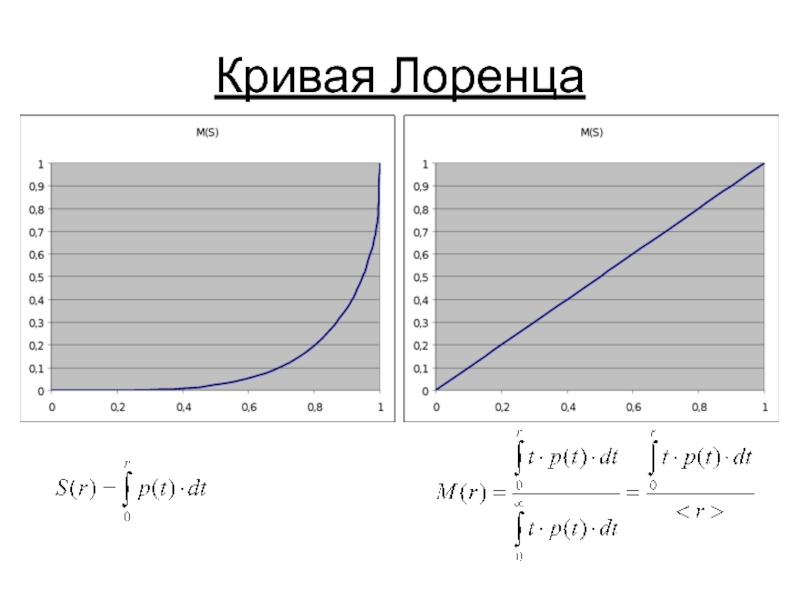
- 3. Кривая Лоренца
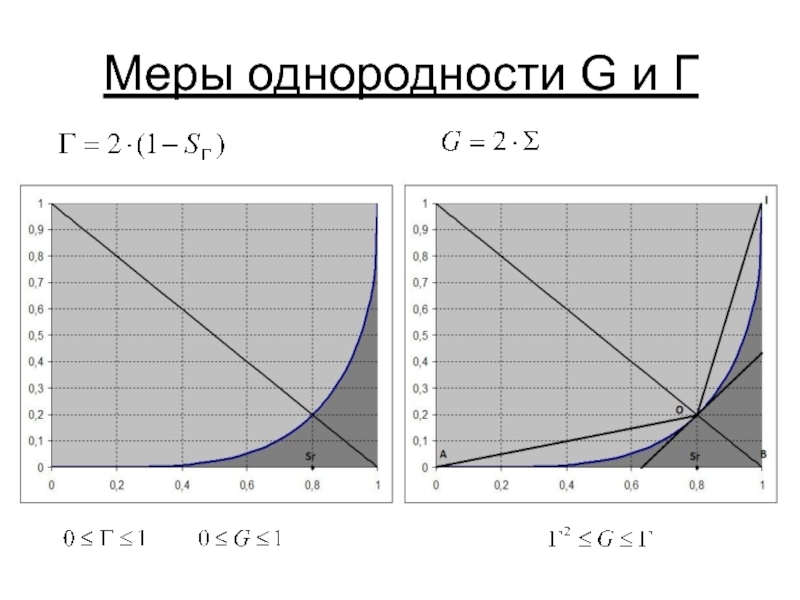
- 4. Меры однородности G и Г
- 5. Три меры неоднородности Меры Г и G
- 6. Свойства меры однородности G
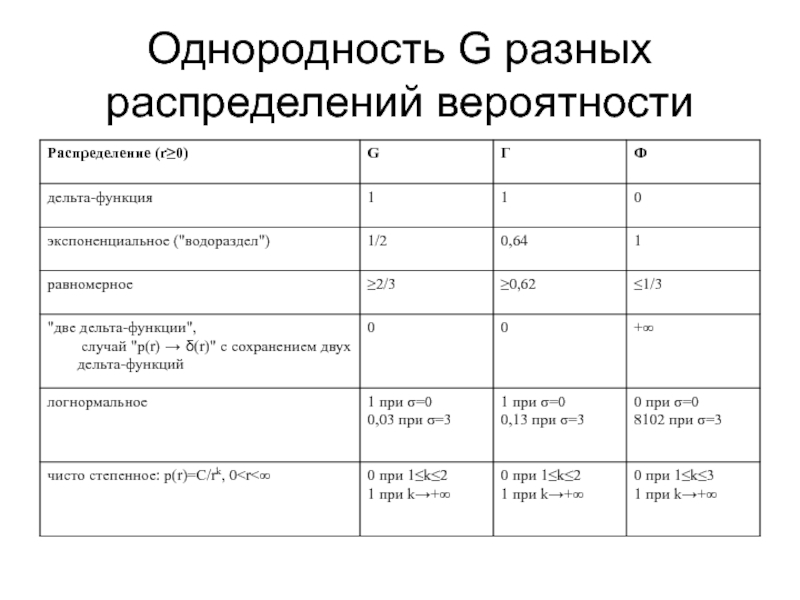
- 7. Однородность G разных распределений вероятности
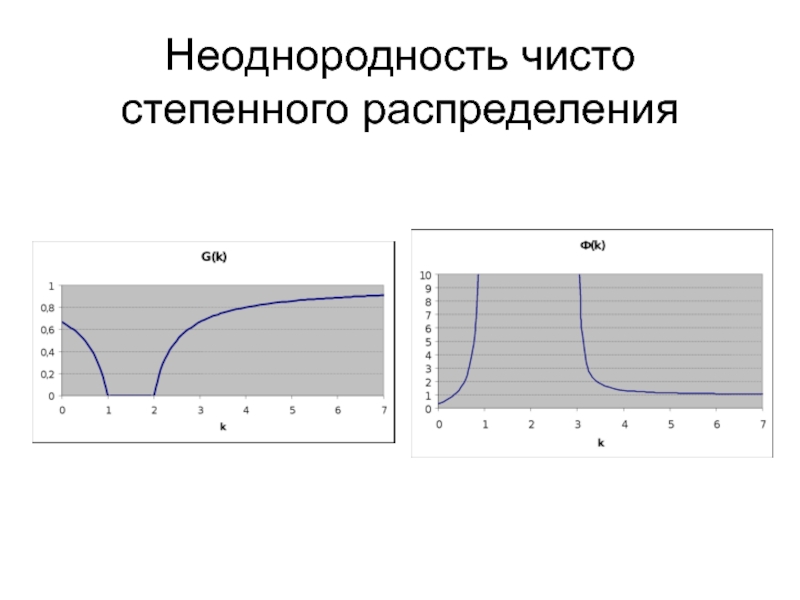
- 8. Неоднородность чисто степенного распределения
- 9. Модель эффекта случайных смещений результата Можно условно
- 10. 2-й случай: r=x+y, где -∞≤r≤+∞ – неоднородность
- 11. Эффект естественного отбора "Побеждают сильнейшие": G
- 12. ЭЕО: Большая неоднородность Скалярное произведение порождает сепарабельное гильбертово пространство:
- 13. Поведение меры однородности G при суммировании гармоник
- 14. ЭЕО: Появление "степенных хвостов" распределений Эффективный
- 15. Дрейф показателя суммы гармоник вниз вплоть до
- 16. Отклонение эфф-го показателя степени от минимального
- 17. Эффективный показатель степени для конечных результатов
- 18. "Чистые" законы распределения не объясняются эффектом естественного
- 19. Условие сокрытия параметров для марковских процессов - произвольная функция
- 20. Чисто степенные распределения для марковских процессов
- 21. Цикл статей "Доказательный менеджмент" 1. Общий подход к
Слайд 1Тема доклада
Почему распределения параметров сложных систем:
часто имеют высокую неоднородность (Принцип
часто имеют степенные хвосты с низкими показателями степени (обычно от 1 до 3)
Причины:
эффект случайного смещения результата (1)
эффект естественного отбора (1+2)
"чистые распределения" (1+2)
Слайд 2Принцип 80/20
20% ассортимента продукции - 80% от общего объема продаж
20%
20% ассортимента продукции или 20% покупателей - 80% прибыли
20% преступников - 80% преступлений
20% водителей - 80% дорожно-транспортных происшествий
20% вступивших в брак - 80% разводов
20% детей - 80% возможностей, предоставляемых системой образования в данной стране
20% площади ковров - 80% воздействий, ведущих к их износу
80% всего времени - 20% имеющейся у вас одежды
80% всех ложных тревог при срабатывании противоугонной сигнализации - 20% возможных причин
Слайд 5Три меры неоднородности
Меры Г и G "работают" только для неотрицательных "r"
Свойства меры Ф проще анализировать
- коэффициент Джини
Слайд 9Модель эффекта случайных смещений результата
Можно условно считать, что:
добавление нового параметра "у"
среднее значение результата не меняется
1-й случай: r=x+y, где r≥0
1) если у "у" корреляция с "х" не отрицательная, то рост всегда будет:
2) возможен случай p(r) → δ(r), G →1,
иначе G≥2/3
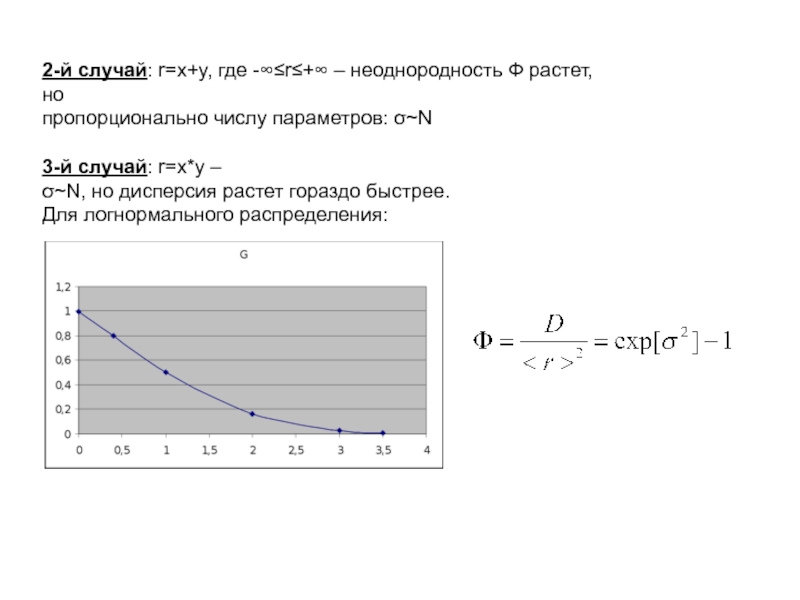
Слайд 102-й случай: r=x+y, где -∞≤r≤+∞ – неоднородность Ф растет, но
пропорционально
3-й случай: r=x*y –
σ~N, но дисперсия растет гораздо быстрее.
Для логнормального распределения:
Слайд 11Эффект естественного отбора
"Побеждают сильнейшие":
G = результат усреднения однородности Gi "гармоник"
Если среди суммируемых "гармоник", т.е. распределений с фиксированным значением параметров , существуют распределения со степенными "хвостами", то итоговое распределение тоже будет иметь степенной хвост, потому что он убывает медленнее.
Слайд 12ЭЕО: Большая неоднородность
Скалярное произведение порождает сепарабельное гильбертово пространство:
Слайд 13Поведение меры однородности G при суммировании гармоник
Сумма гармоник:
- "длина
То есть побеждают наибольшие
Слайд 14ЭЕО: Появление "степенных хвостов" распределений
Эффективный показатель степени:
"Степенное усреднение":
В дискретном
Слайд 15Дрейф показателя суммы гармоник вниз вплоть до наименьшего из показателей
"Степенная
Слайд 18"Чистые" законы распределения
не объясняются эффектом естественного отбора
объясняются эффектом случайных смещений параметра
Слайд 20Чисто степенные распределения для марковских процессов
Разумно предположить, что
Оператор "А" является масштабно-инвариантным:
глобальная масштабная инвариантность может существовать только если объекты не взаимодействуют или эволюционирует один объект
локальная масштабная инвариантность может возникнуть, только если на объекты влияют параметры всей совокупности других объектов как целое: "температура", число, "давление"
Оператор "В" в общем случае не является масштабно-инвариантным и, соответственно, не будет масштабно-инвариантным и итоговый оператор "ВА".
Слайд 21Цикл статей "Доказательный менеджмент"
1. Общий подход к расчету проектов
2. Критика книги "От хорошего
3. Расчет эффективностей и их использование
4. Тестирование в бизнесе
5. Инновация как враг прибыльного бизнеса
6. Как объяснить Принцип 80/20 с помощью эффектов "естественного отбора" и случайных смещений результата
7. Оценка вероятностей человеком – дважды неожиданные эффекты
8. Система Тойоты и реинжиниринг – чем могут помочь численные модели?