- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Распознавание изображений. Выделение признаков презентация
Содержание
- 1. Распознавание изображений. Выделение признаков
- 2. ~ 90% информации человек получает через зрение
- 3. Распознавание изображений В XXI веке появились большие
- 4. За последние 10 лет произошел огромный толчок
- 5. Сужаем класс задач Наши условия: Есть изображение
- 6. Общий алгоритм
- 7. Фильтрация от шума На всех реальных изображениях
- 8. Фильтр низких частот Свертка с прямоугольным окном
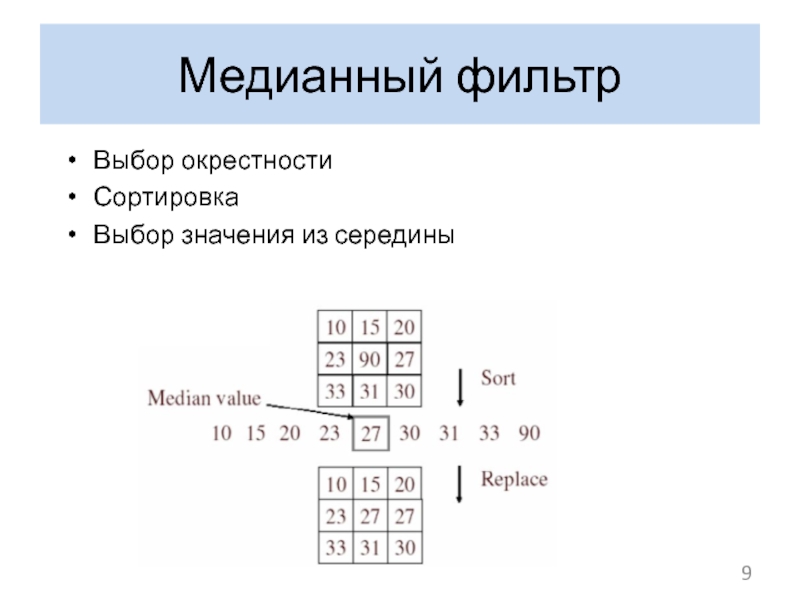
- 9. Выбор окрестности Сортировка Выбор значения из середины Медианный фильтр
- 10. Фильтрация от шума
- 11. Метод наращивания и соединения областей Исходное изображение
- 12. Результат сегментации
- 13. Есть картинка, и что? Компьютер понимает только
- 14. Очень много информации На обычном hd снимке
- 15. Проблемы освещенности
- 16. Искажения перспективы
- 17. Аберрации линзы (рыбий глаз)
- 18. Вариация формы
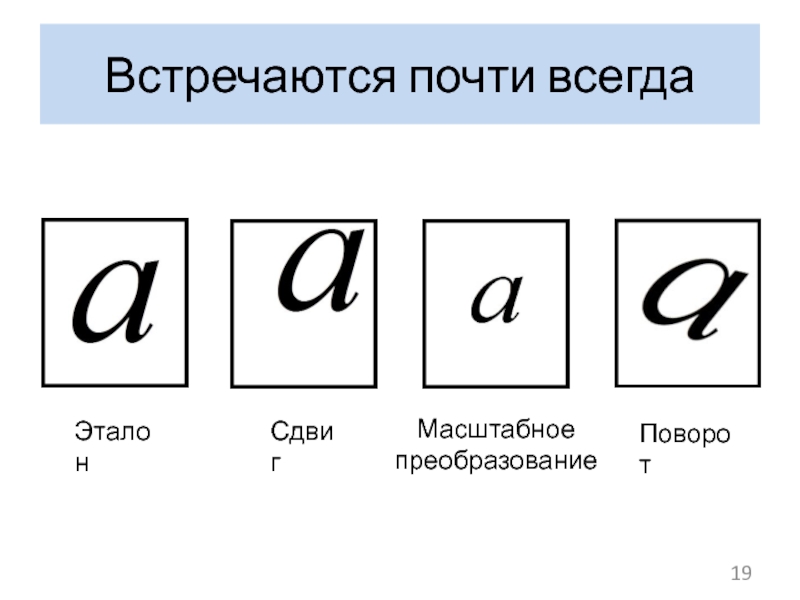
- 19. Встречаются почти всегда Эталон Сдвиг Масштабное преобразование Поворот
- 20. Выделение признаков для изображений символов Предположения: Изображение
- 21. Математическое представление изображения Это функция двух переменных (непрерывный случай) Это матрица (дискретный случай)
- 22. Математическое представление изображения Справедливы: Сложение Вычитание Умножение Деление Возведение в степень И т.д.
- 23. Физическое представление изображения Это плоская фигура (непрерывный
- 24. Инвариантность относительно сдвига Буква – это твердое
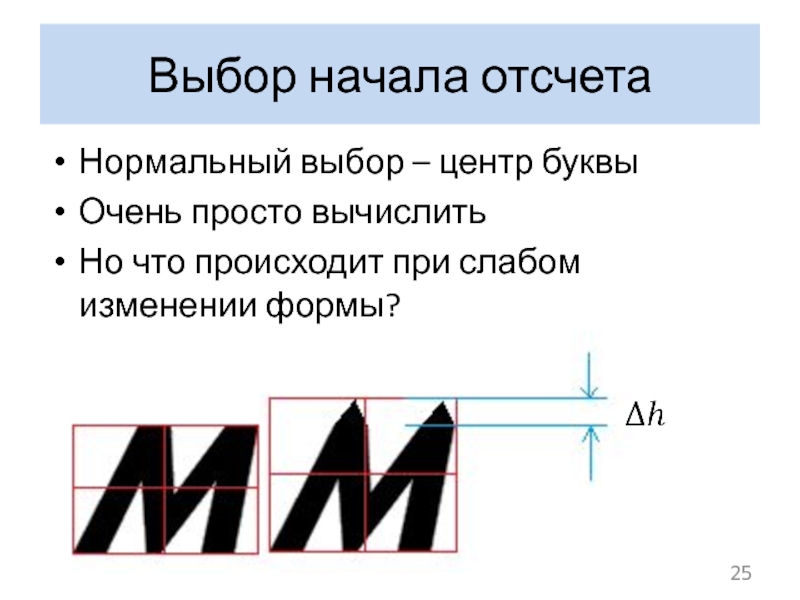
- 25. Выбор начала отсчета Нормальный выбор – центр
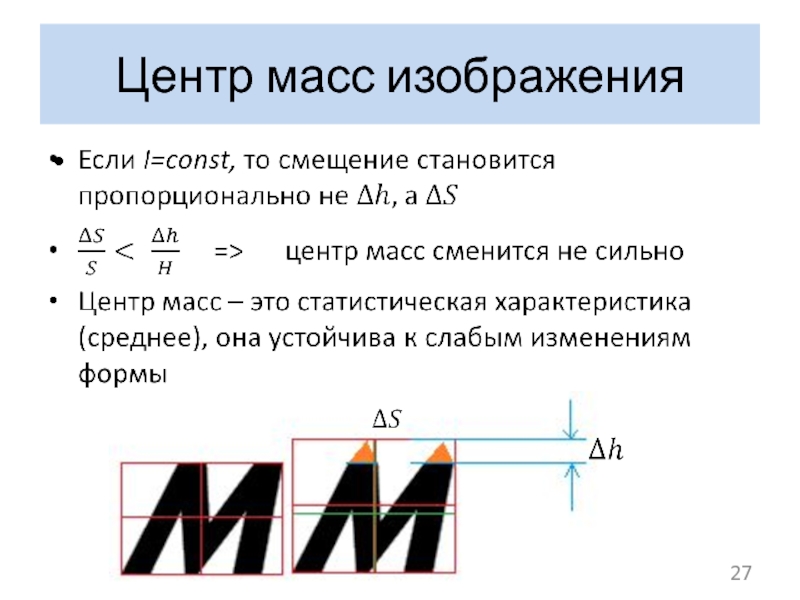
- 26. Центр масс изображения
- 27. Центр масс изображения
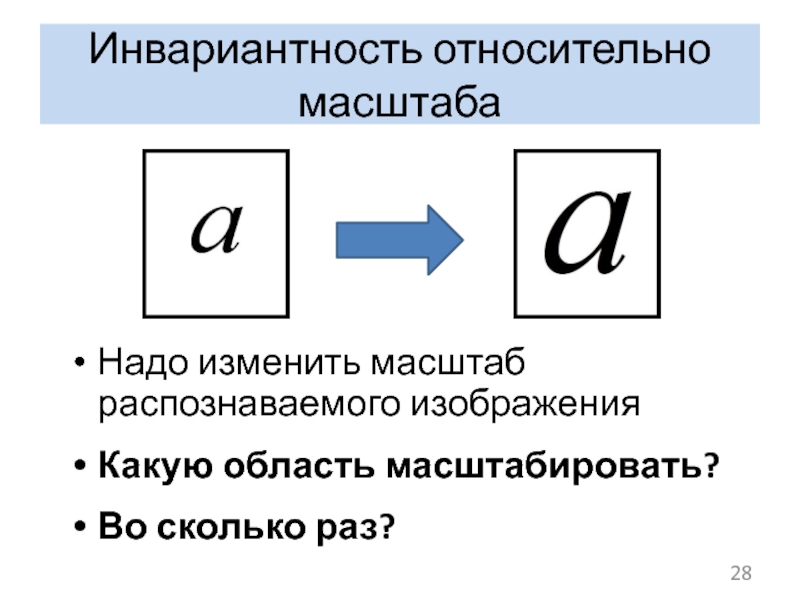
- 28. Инвариантность относительно масштаба Надо изменить масштаб распознаваемого
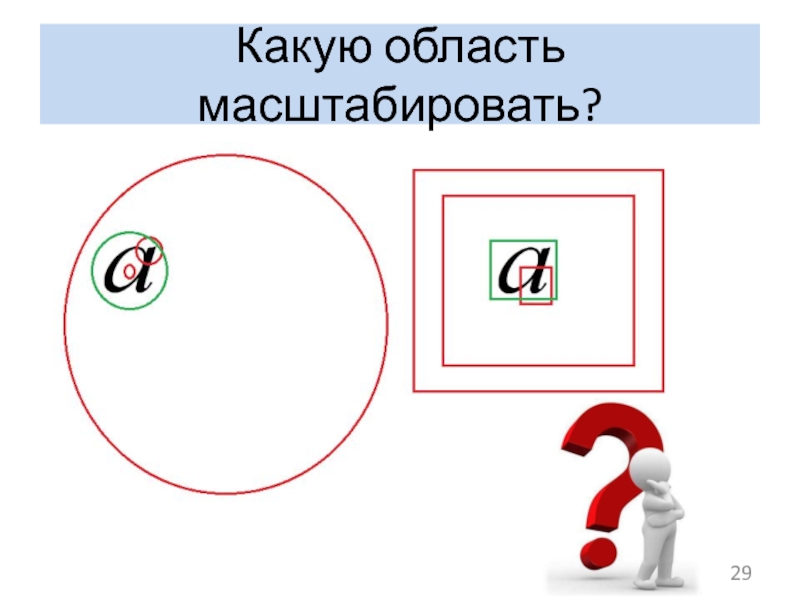
- 29. Какую область масштабировать?
- 30. Какую область масштабировать? Она должна быть связана
- 31. Статистические характеристики Удобно рассмотреть распределение пикселей по
- 32. Статистические характеристики Область точно не надо брать
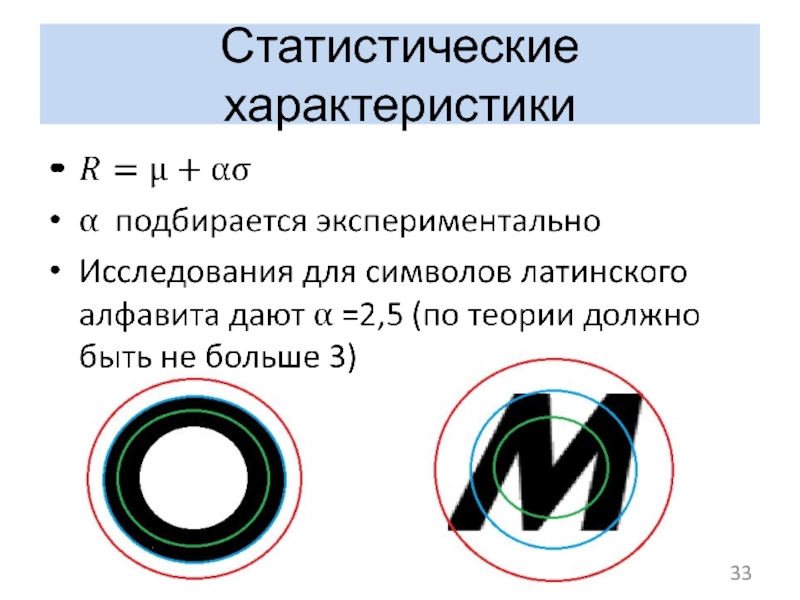
- 33. Статистические характеристики
- 34. Во сколько раз масштабировать? Под размер шаблона
- 35. Не случится ли беды? Делаем масштабирование в
- 36. Не случится ли беды? Появление высоких частот
- 37. Этапы масштабной нормализации Исходный символ Свертка с Гауссовым фильтром Отмасштабированный символ
- 38. Линейная алгебра Функция это элемент гильбертова пространства.
- 39. Разложение векторов Если размерность базиса (кол-во векторов
- 40. Моменты В функциональном пространстве скалярное произведение f(x)
- 41. Базисы Не ортогональный: Регулярный базис Регулярные моменты
- 42. Полиномы Цернике Ортогональность Легко восстановить изображение Коэффициенты
- 43. Восстановление изображения Чтобы восстановить изображение надо найти
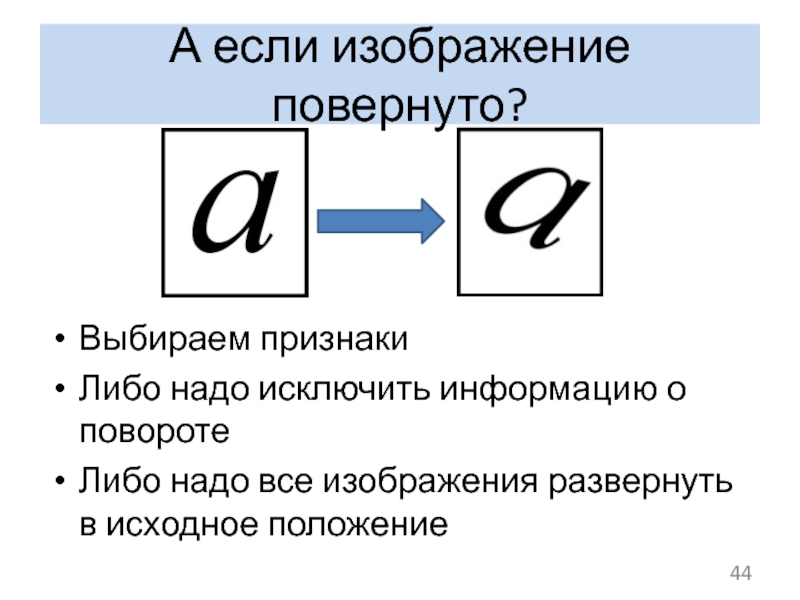
- 44. А если изображение повернуто? Выбираем признаки Либо
- 45. Поворот в исходное положение Вспомним физическую интерпретацию
- 46. Определение поворота по собственной системе координат Рассчитывается
- 47. Модуль моментов Возьмем модуль от моментов Цернике
- 48. Выбор признаков Коэффициент с n=0 вносит большую
Слайд 1 Распознавание изображений:
Выделение признаков
подготовил: аспирант 1 года
Чуманкин Юрий Евгеньевич
Нижегородский государственный университет им.
Кафедра информационных технологий в физических исследованиях
Слайд 2~ 90% информации человек получает через зрение
Это очень информативный источник
Множество рутинной
Гаишник высматривает нарушителей
Работник завода ищет бракованные детали
Охранник сверяет фото на пропуске с лицом человека
Было бы здорово автоматизировать эту работу
Распознавание изображений
Слайд 3Распознавание изображений
В XXI веке появились большие вычислительные мощности
Получать цифровые изображения стало
Слайд 4За последние 10 лет произошел огромный толчок
КЗ нашло свое применение:
Распознавание людей
(отпечаток
Контроль подлинности (банкнот, документов)
Распознавание текста (ABBY)
Интеллектуальное видеонаблюдение (системы безопасности, письма счастья)
Контроль качества (подсчет длины очереди, поиск течи в трубе)
Распознавание изображений
Слайд 5Сужаем класс задач
Наши условия:
Есть изображение
На нем есть объект
Необходимо отнести его к
Пример:
Распознать букву
Распознать чей отпечаток
Задача распознавания
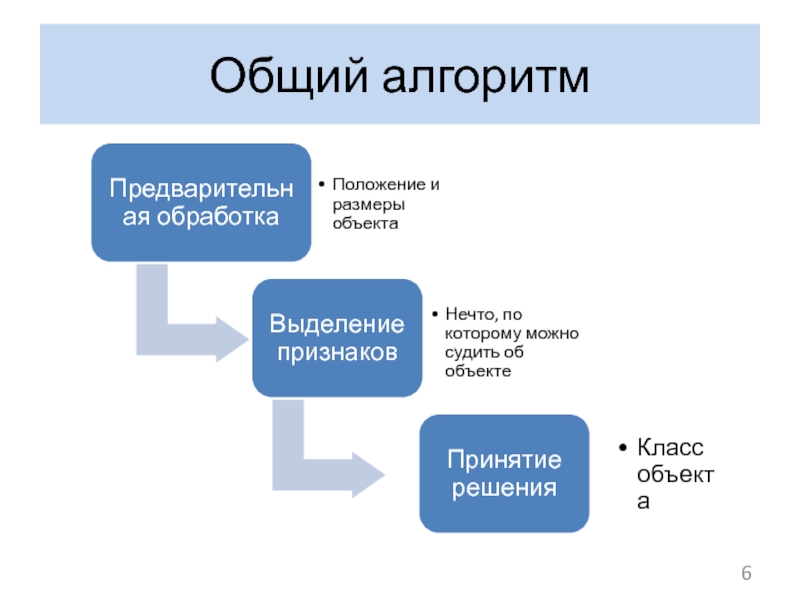
Слайд 7Фильтрация от шума
На всех реальных изображениях присутствует шум
Шум распределен
в широкой
Не понятно как отделить его от изображения
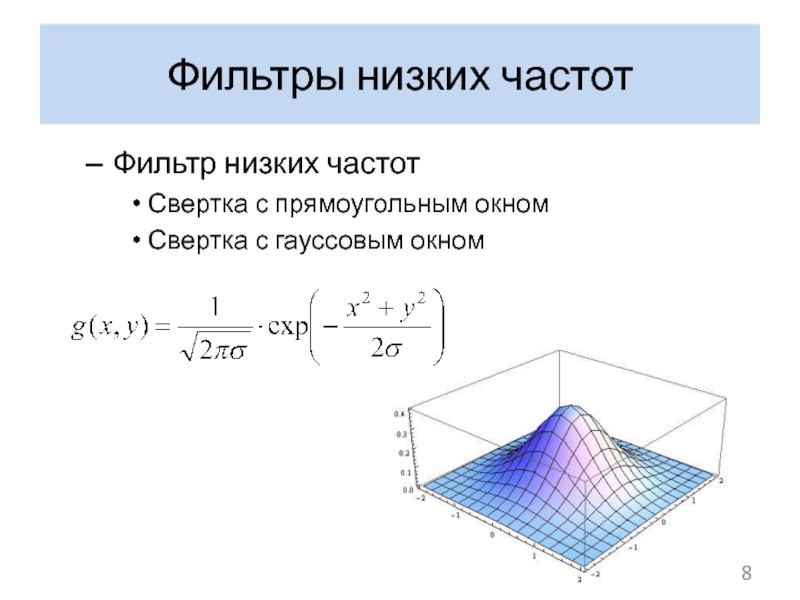
Слайд 8Фильтр низких частот
Свертка с прямоугольным окном
Свертка с гауссовым окном
Фильтры низких частот
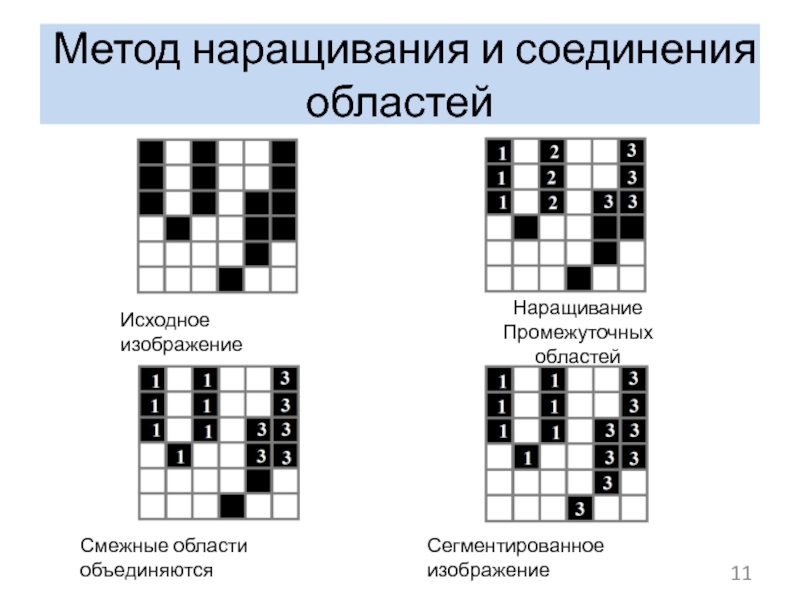
Слайд 11Метод наращивания и соединения областей
Исходное изображение
Наращивание
Промежуточных областей
Смежные области объединяются
Сегментированное изображение
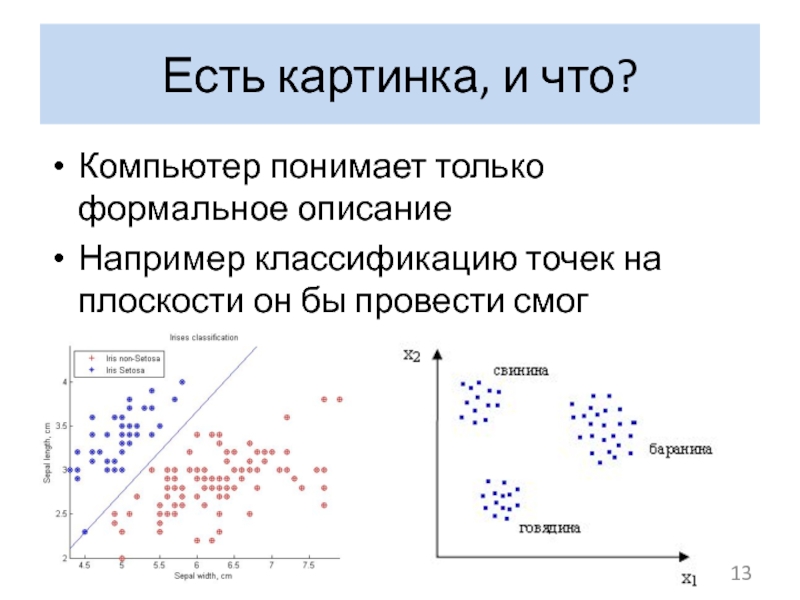
Слайд 13Есть картинка, и что?
Компьютер понимает только
формальное описание
Например классификацию точек на плоскости
Слайд 14Очень много информации
На обычном hd снимке 1280 * 720 ~ 1
Сложно обрабатывать такие большие массивы данных
Не вся информация является полезной для распознавания
Есть информация которая сбивает с толку
Что отличает изображение от точки в пространстве?
Слайд 20Выделение признаков для изображений символов
Предположения:
Изображение полутоновое
Символ на картинке один
Задача:
Сопоставить изображению набор
Учесть смещение символа
Учесть символы разных масштабов
Учесть символы повернутые на разный угол
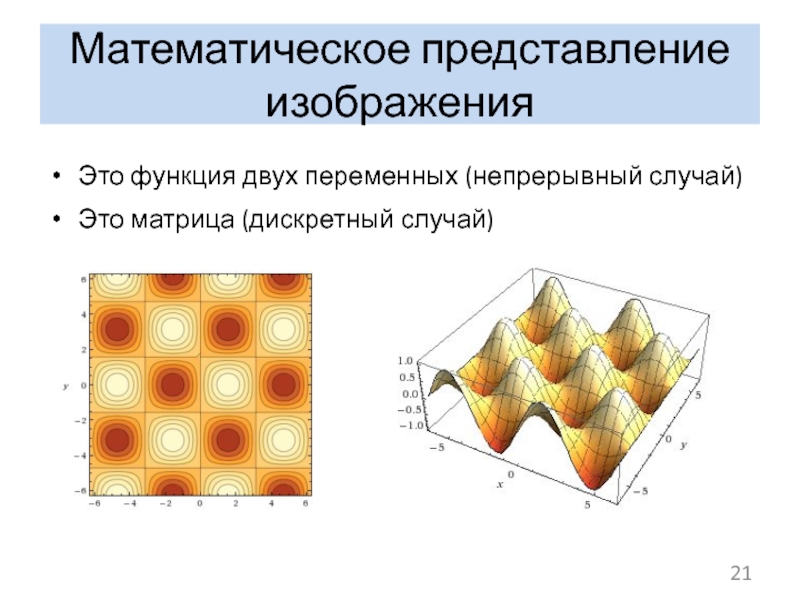
Слайд 21Математическое представление изображения
Это функция двух переменных (непрерывный случай)
Это матрица (дискретный случай)
Слайд 22Математическое представление изображения
Справедливы:
Сложение
Вычитание
Умножение
Деление
Возведение в степень
И т.д.
Слайд 23Физическое представление изображения
Это плоская фигура (непрерывный случай)
Это система материальных точек (дискретный
Чем светлее фрагмент, тем больше он весит
Интенсивность (I) выступает в роли плотности
Здесь и далее рассматриваем буквы
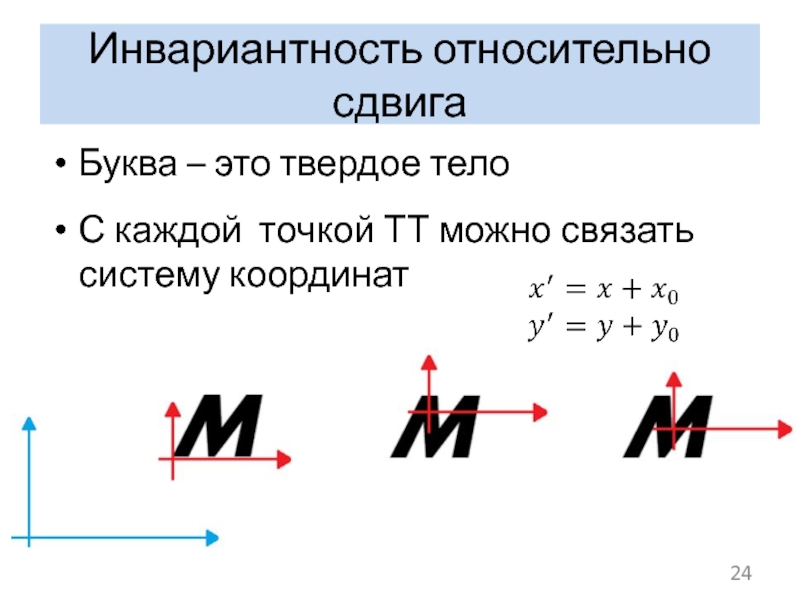
Слайд 24Инвариантность относительно сдвига
Буква – это твердое тело
С каждой точкой ТТ можно
Слайд 25Выбор начала отсчета
Нормальный выбор – центр буквы
Очень просто вычислить
Но что происходит
Слайд 28Инвариантность относительно масштаба
Надо изменить масштаб распознаваемого изображения
Какую область масштабировать?
Во сколько раз?
Слайд 30Какую область масштабировать?
Она должна быть связана с размерами символа
Можно выбрать описанный
Недостатки все те же, что и раньше
Выгоднее опираться на статистические характеристики
Слайд 31Статистические характеристики
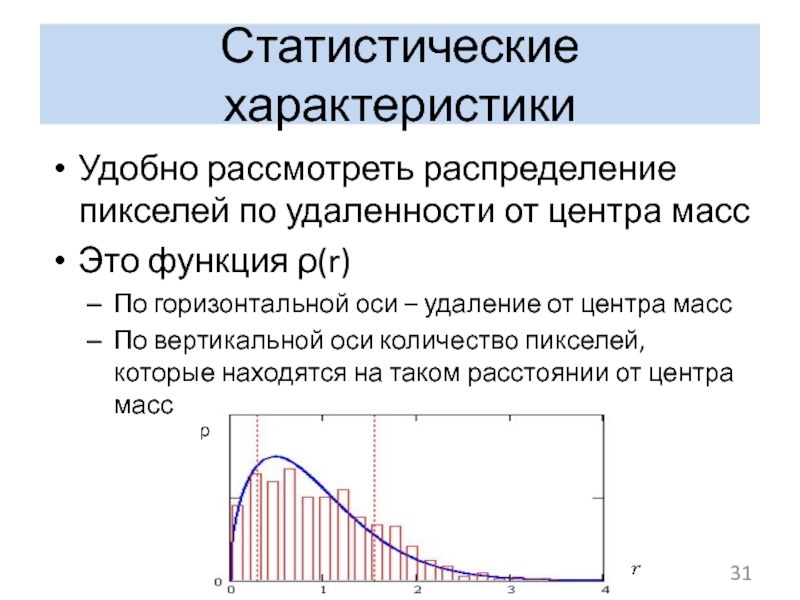
Удобно рассмотреть распределение пикселей по удаленности от центра масс
Это функция
По горизонтальной оси – удаление от центра масс
По вертикальной оси количество пикселей, которые находятся на таком расстоянии от центра масс
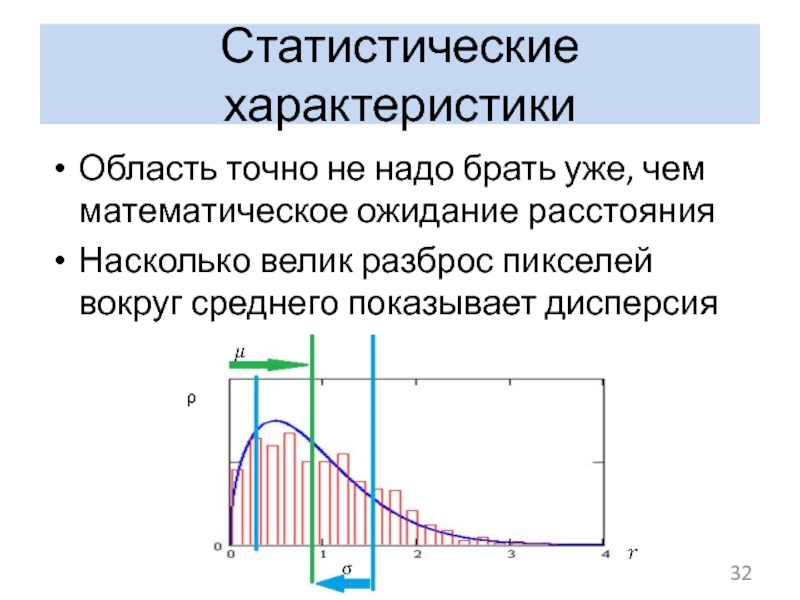
Слайд 32Статистические характеристики
Область точно не надо брать уже, чем математическое ожидание расстояния
Насколько
Слайд 34Во сколько раз масштабировать?
Под размер шаблона с которым будет делаться сравнение
Шаблон
не слишком маленьким
Теряются детали
Не слишком большим
Долго обрабатывать
Исследования показали что оптимальный размер 30 пикселей
Слайд 35Не случится ли беды?
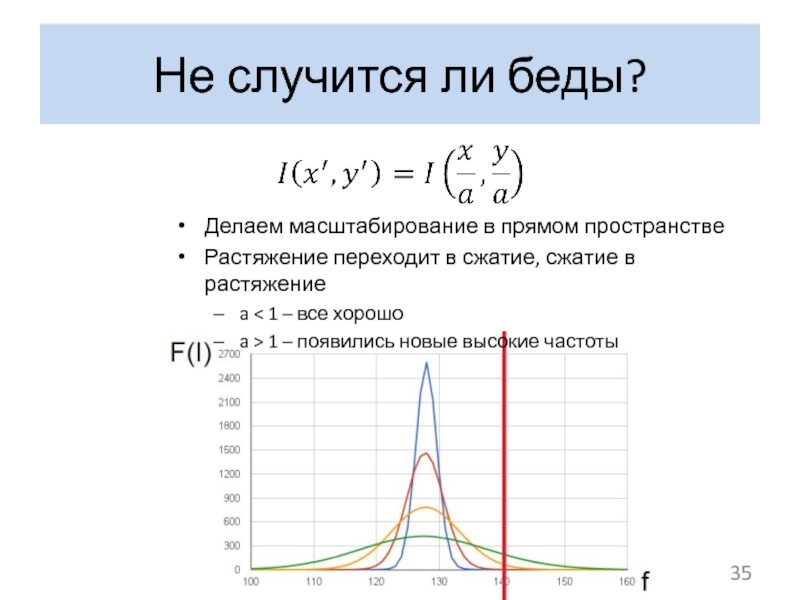
Делаем масштабирование в прямом пространстве
Растяжение переходит в сжатие,
a < 1 – все хорошо
a > 1 – появились новые высокие частоты
Слайд 36Не случится ли беды?
Появление высоких частот при фиксированной частоте дискретизации может
Это означает потерю информации
Чтобы этого не произошло надо убрать высокие частоты из исходной картинки
Слайд 37Этапы масштабной нормализации
Исходный символ
Свертка с
Гауссовым фильтром
Отмасштабированный
символ
Слайд 38Линейная алгебра
Функция это элемент гильбертова пространства. Как вектор.
Скалярное произведение:
Ортонормированный базис:
Слайд 39Разложение векторов
Если размерность базиса (кол-во векторов в нем) совпадает с размерностью
В общем случае:
Для ортонормированного базиса
Слайд 40Моменты
В функциональном пространстве скалярное произведение f(x) на g(x) назвали:
Момент f(x) относительно
Базисы есть разные, еще момент называют по имени базиса
Какие базисы используются?
Слайд 41Базисы
Не ортогональный:
Регулярный базис
Регулярные моменты
Ортогональные
Базис Цернике
Моменты Цернике
Базис Уолша
Моменты Уолша
Слайд 42Полиномы Цернике
Ортогональность
Легко восстановить изображение
Коэффициенты слабо коррелированы
Модуль коэффициентов
инвариантен к
Слайд 43Восстановление изображения
Чтобы восстановить изображение надо найти коэффициенты
Формула для восстановления
Слайд 44А если изображение повернуто?
Выбираем признаки
Либо надо исключить информацию о повороте
Либо надо
Слайд 45Поворот в исходное положение
Вспомним физическую интерпретацию изображения
Как у любого твердого тела,
у
Слайд 46Определение поворота по собственной системе координат
Рассчитывается тензор инерции
Определяются собственные направления
Сравниваются направления
Слайд 48Выбор признаков
Коэффициент с n=0 вносит большую ошибку
Коэффициент с n=1 пропорционален rc
nmax
Всего 48 признаков
Они будут инвариантны к повороту