- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проверка гипотез. Основы ДА презентация
Содержание
- 1. Проверка гипотез. Основы ДА
- 2. Цели Что делать, если независимая переменная
- 3. Независимая переменная имеет больше двух уровней Действительно
- 4. Независимая переменная имеет больше двух уровней Нашей
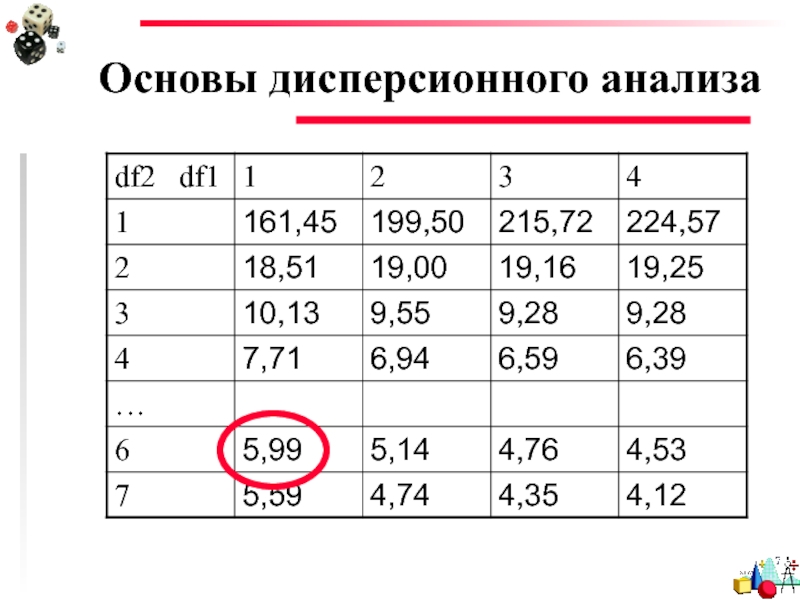
- 5. Независимая переменная имеет больше двух уровней 6
- 6. Независимая переменная имеет больше двух уровней Вероятность
- 7. Независимая переменная имеет больше двух уровней Для
- 8. Независимая переменная имеет больше двух уровней Что делать? Применять специальные критерии!
- 9. Основы дисперсионного анализа В качестве такого критерия для параметрических данных используется ДИСПЕРСИОННЫЙ АНАЛИЗ
- 10. Основы дисперсионного анализа Дисперсионный анализ – это
- 11. Основы дисперсионного анализа Дисперсионный анализ иногда в
- 12. Основы дисперсионного анализа Рассмотрим идеи однофакторного дисперсионного
- 13. Понятие о сумме квадратов Предположим, что мы
- 14. Понятие о сумме квадратов
- 15. Понятие о сумме квадратов Теперь, если мы
- 16. Понятие о сумме квадратов Внутригрупповая сумма квадратов
- 17. Понятие о сумме квадратов ЛЕВШИ
- 18. Понятие о сумме квадратов Внутригрупповая сумма квадратов
- 19. Понятие о сумме квадратов Межгрупповая сумма квадратов
- 20. Понятие о сумме квадратов Общая сумма квадратов
- 21. Получение оценок дисперсий Значимость разницы между этими
- 22. Получение оценок дисперсий Если межгрупповая дисперсия (т.е.
- 23. Получение оценок дисперсий Таким образом, проверка нуль-гипотезы
- 24. Получение оценок дисперсий Степени свободы для межгрупповой
- 25. Получение оценок дисперсий Степени свободы для внутригрупповой
- 26. Основы дисперсионного анализа
- 27. Основы дисперсионного анализа
- 28. Основы дисперсионного анализа Fэмп
- 29. Основы дисперсионного анализа
- 30. Основы дисперсионного анализа Ограничения
- 31. Основы дисперсионного анализа Действительно ли холерики и сангвиники более агрессивны, чем флегматики и меланхолики? F(3,342)=12,87; p
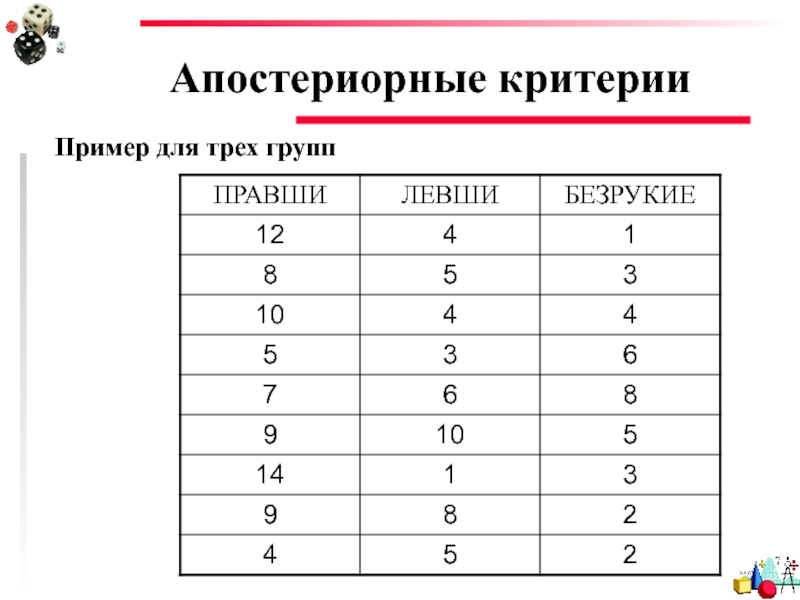
- 32. Апостериорные критерии Пример для трех групп
- 33. Апостериорные критерии
- 34. Апостериорные критерии
- 35. Апостериорные критерии
- 36. Апостериорные критерии H0: μ1= μ2 H0: μ1= μ3 H0: μ3= μ2
- 37. Апостериорные критерии Критерий Тьюки (Tukey) – HSD
- 38. Апостериорные критерии Считаем таблицу разниц между средними групп
- 39. Апостериорные критерии qα для α=0,05
- 40. Апостериорные критерии Критерий Тьюки (Tukey) – HSD
- 41. Апостериорные критерии HSD=3,18
- 42. Апостериорные критерии HSD=3,18
- 43. Апостериорные критерии
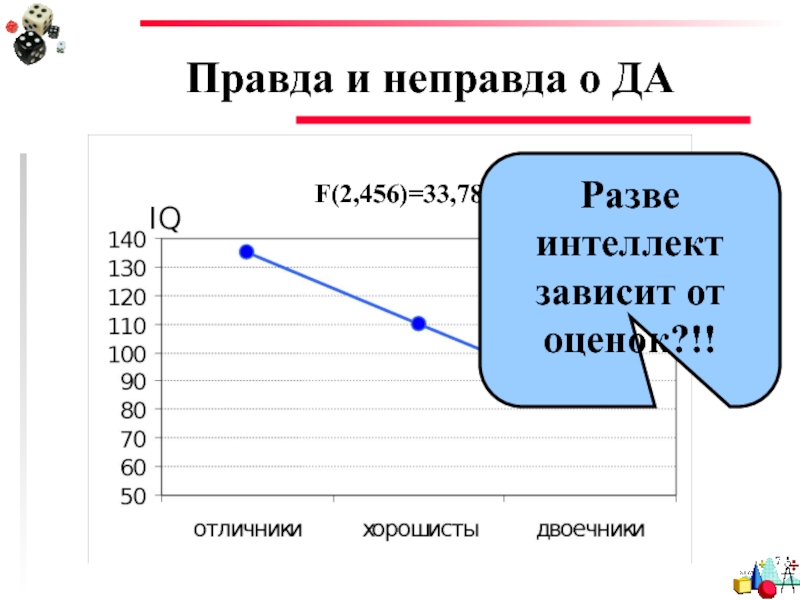
- 44. Правда и неправда о ДА Дисперсионный анализ
- 45. F(2,456)=33,78; p
- 46. Самостоятельная работа К следующему занятию прочитать: Радчикова
- 47. Исследование с несколькими НП Эффект одной независимой
- 48. Исследование с несколькими НП Взаимодействие − это
- 49. Исследование с несколькими НП Взаимодействие показывает, зависит
- 50. Исследование с несколькими НП Нельзя интерпретировать результаты исследования, не принимая во внимание взаимодействие!
- 51. Исследование с несколькими НП Пример. Психолог провел
- 52. Исследование с несколькими НП В этом исследовании
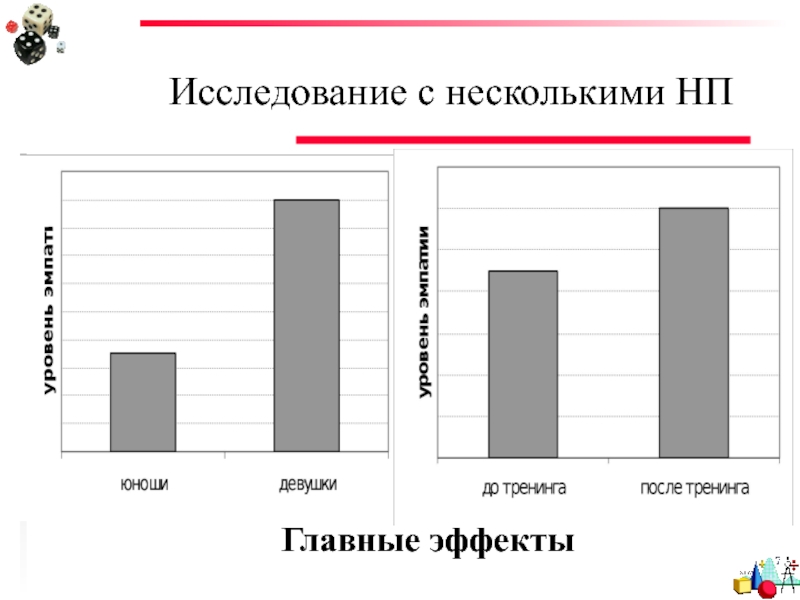
- 53. Исследование с несколькими НП Главные эффекты
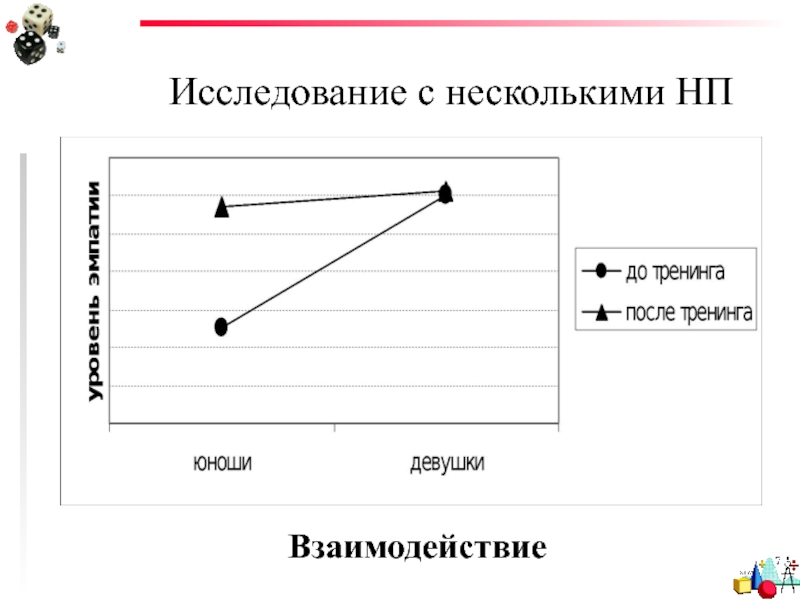
- 54. Исследование с несколькими НП Взаимодействие
- 55. Исследование с несколькими НП
- 56. Исследование с несколькими НП
- 57. Исследование с несколькими НП
- 58. Стой, Подумай, Примени
- 59. Стой, Подумай, Примени
- 60. Стой, Подумай, Примени
- 61. Стой, Подумай, Примени
- 62. Стой, Подумай, Примени
- 63. Стой, Подумай, Примени
- 64. Стой, Подумай, Примени
- 65. Стой, Подумай, Примени
- 66. Стой, Подумай, Примени
- 67. Стой, Подумай, Примени
- 68. Стой, Подумай, Примени
- 69. Самостоятельная работа К практическому занятию по ДА
- 70. СПАСИБО ЗА ВНИМАНИЕ!
- 71. Многомерный ДА Используется тогда, когда мы хотим
Слайд 2Цели
Что делать, если независимая переменная имеет больше двух уровней?
Что делать,
Что делать, если в эксперименте более одной зависимой переменной?
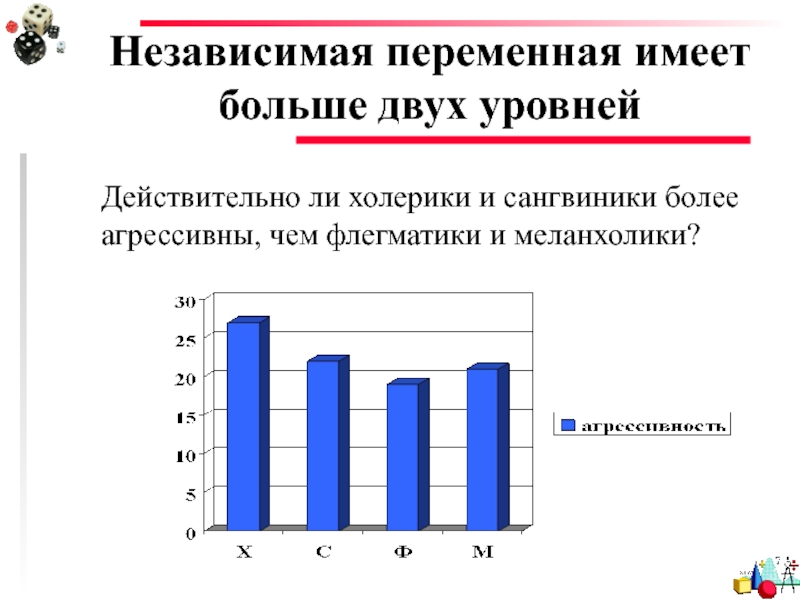
Слайд 3Независимая переменная имеет больше двух уровней
Действительно ли холерики и сангвиники более
Слайд 4Независимая переменная имеет больше двух уровней
Нашей задачей является избегание ошибки I
Если мы примем уровень статистической значимости равным 0,05, мы согласимся принять риск ошибиться в 5 случаях из 100. Когда происходит много сравнений, этот риск увеличивается.
Слайд 5Независимая переменная имеет больше двух уровней
6 сравнений:
Вероятность сделать ошибку при каждом
Тогда вероятность не сделать ошибку
1-0,05=0,95.
Слайд 6Независимая переменная имеет больше двух уровней
Вероятность не сделать ошибку во всех
(0,95)6=0,74.
А вероятность допустить ошибку хотя бы в одном сравнении равна
1-0,74=0,26 !
Слайд 7Независимая переменная имеет больше двух уровней
Для 10 сравнений вероятность сделать по
для 20 сравнений – уже 0,64!!!
Слайд 9Основы дисперсионного анализа
В качестве такого критерия для параметрических данных используется
ДИСПЕРСИОННЫЙ
Слайд 10Основы дисперсионного анализа
Дисперсионный анализ – это процедура, которая позволяет сравнивать средние
Дисперсионный анализ позволяет ответить на вопрос: «Значимо ли различаются средние значения зависимой переменной при разных уровнях независимой переменной?»
Слайд 11Основы дисперсионного анализа
Дисперсионный анализ иногда в литературе называется ANOVA (от английского
Слайд 12Основы дисперсионного анализа
Рассмотрим идеи однофакторного дисперсионного анализа на примере для несвязных
В этом случае группы, которые мы сравниваем, представляют различные уровни (значения) одной независимой переменной (или фактора).
Фактор и независимая переменная являются в данном случае синонимами.
Слайд 13Понятие о сумме квадратов
Предположим, что мы провели исследование, где две группы
Высокий набранный балл свидетельствует о большем удобстве.
Проверим гипотезу о том, что нет зависимости оценки удобства работы на компьютере от доминантной руки.
Слайд 15Понятие о сумме квадратов
Теперь, если мы вычтем общее среднее из каждого
SSобщ (SS – sum of squares)
SSОБЩ = (1-6)2+(2-6)2+(5-6)2+(8-6)2+
+(6-6)2+(7-6)2+(8-6)2+(10-6)2=72
Слайд 16Понятие о сумме квадратов
Внутригрупповая сумма квадратов – это сумма сумм квадратов,
Слайд 17Понятие о сумме квадратов
ЛЕВШИ ПРАВШИ
Источником внутригрупповой изменчивости являются
Слайд 18Понятие о сумме квадратов
Внутригрупповая сумма квадратов = сумма квадратов группы 1
SSВ/Г=SSЛЕВ+SSПРАВ
Слайд 19Понятие о сумме квадратов
Межгрупповая сумма квадратов – это сумма квадратов отклонений
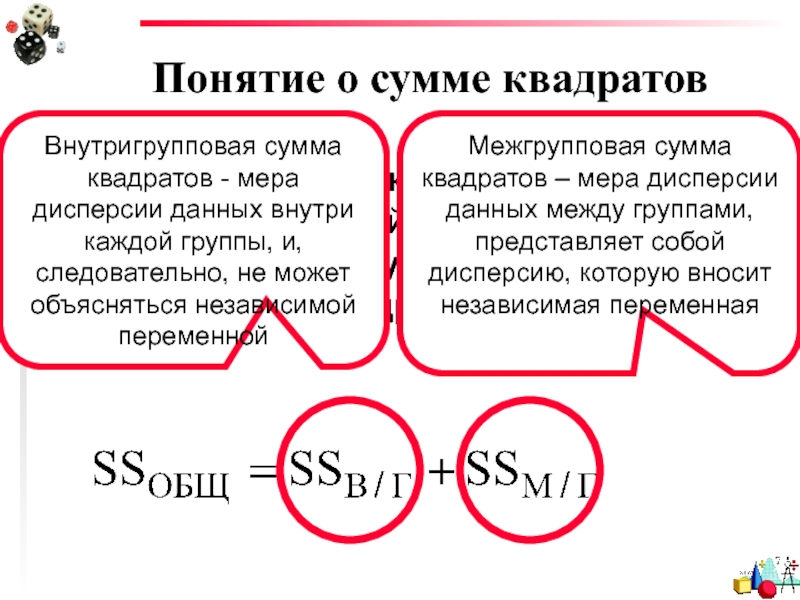
Слайд 20Понятие о сумме квадратов
Общая сумма квадратов равна внутригрупповой сумме квадратов плюс
Внутригрупповая сумма квадратов - мера дисперсии данных внутри каждой группы, и, следовательно, не может объясняться независимой переменной
Межгрупповая сумма квадратов – мера дисперсии данных между группами, представляет собой дисперсию, которую вносит независимая переменная
Слайд 21Получение оценок дисперсий
Значимость разницы между этими двумя оценками дисперсии (суммами квадратов)
Слайд 22Получение оценок дисперсий
Если межгрупповая дисперсия (т.е. разница между средними групп) велика
Если межгрупповая дисперсия мала относительно внутригрупповой дисперсии, число F достаточно мало.
Слайд 23Получение оценок дисперсий
Таким образом, проверка нуль-гипотезы требует вычисления отношения межгрупповой и
Но! Оба значения растут с ростом размера выборки. Поэтому следует делить обе суммы квадратов на соответствующие степени свободы.
Слайд 24Получение оценок дисперсий
Степени свободы для межгрупповой суммы квадратов – что число
dfМ/Г=k-1
В нашем случае k=2, dfМ/Г =2-1=1
Следовательно, средняя сумма квадратов MSМ/Г (mean square):
Слайд 25Получение оценок дисперсий
Степени свободы для внутригрупповой суммы квадратов – это общее
DfВ/Г=N-k=8-2=6
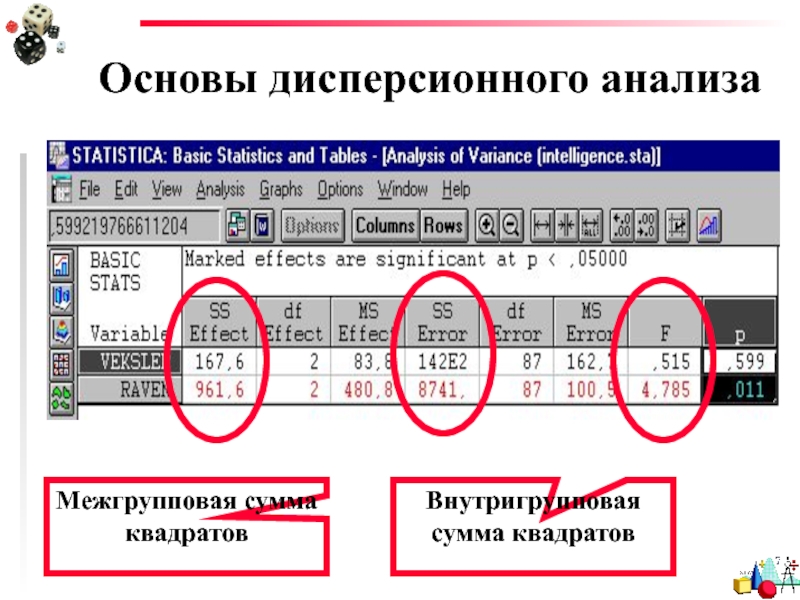
Слайд 28Основы дисперсионного анализа
Fэмп
Слайд 30Основы дисперсионного анализа
Ограничения и предположения ДА
дисперсии в сравниваемых группах должны быть
выборки должны быть случайны и независимы
зависимая переменная должна быть, по крайней мере, интервальной, и нормально распределена в каждой группе.
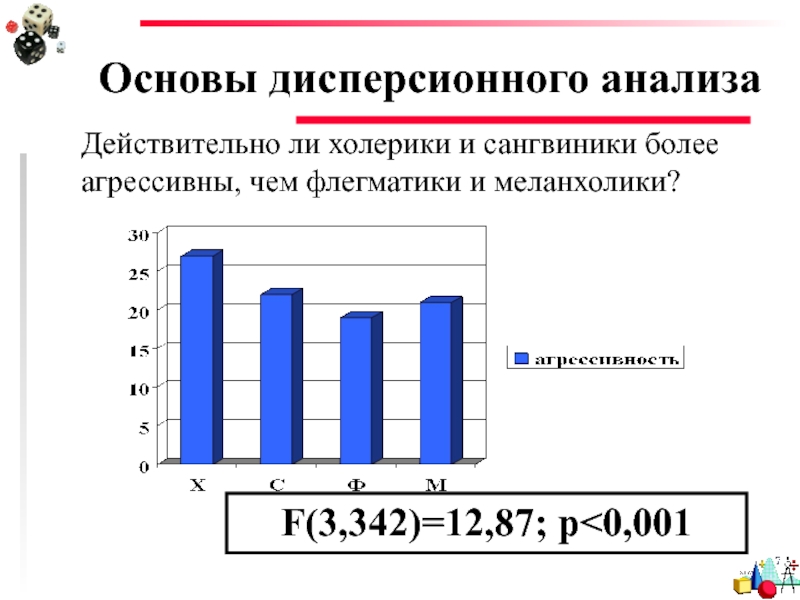
Слайд 31Основы дисперсионного анализа
Действительно ли холерики и сангвиники более агрессивны, чем флегматики
F(3,342)=12,87; p<0,001
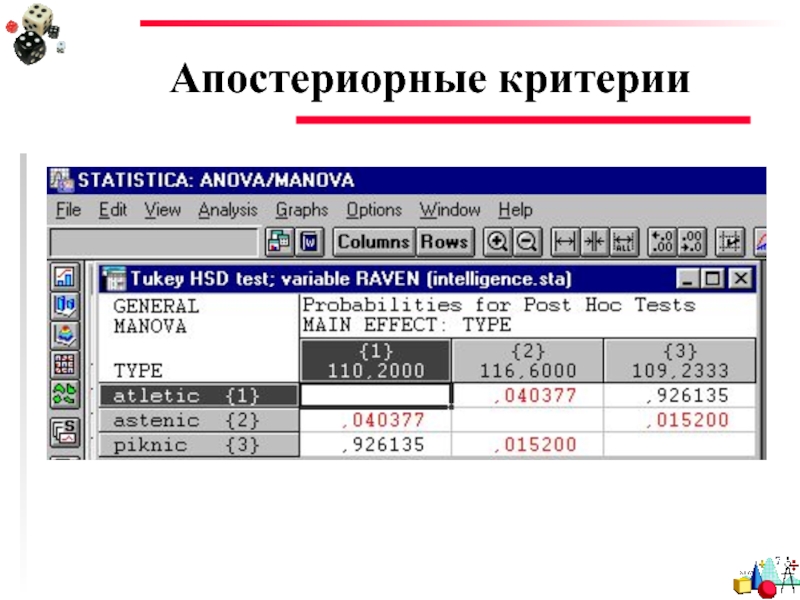
Слайд 37Апостериорные критерии
Критерий Тьюки (Tukey) – HSD (honestly significant difference)
N – число
qα - значение из специальной таблицы для уровня значимости α, числа сравнений k и dfв/г
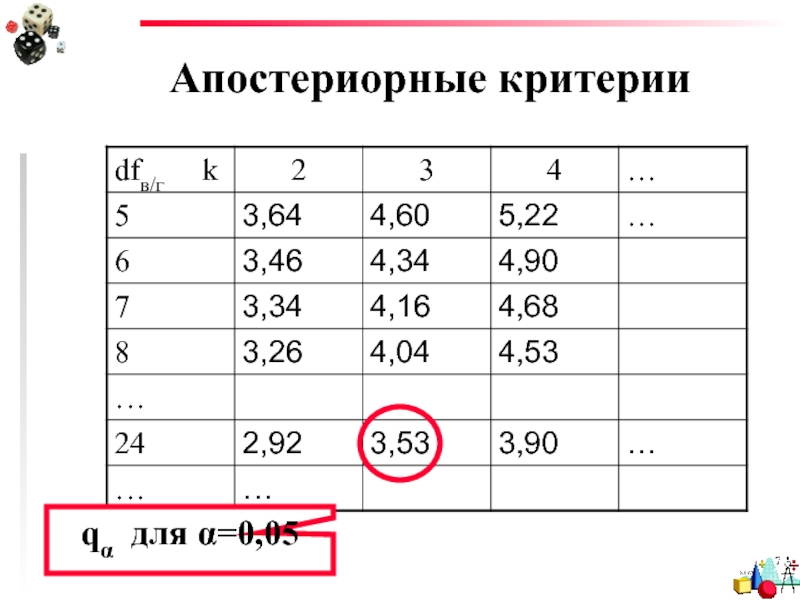
Слайд 40Апостериорные критерии
Критерий Тьюки (Tukey) – HSD (honestly significant difference)
N =9
qα =3,53
Слайд 44Правда и неправда о ДА
Дисперсионный анализ
НЕ
показывает причину!
И никаким образом
Слайд 46Самостоятельная работа
К следующему занятию прочитать:
Радчикова Н.П. Объем памяти и размер алфавита…//
(есть в электронном виде)
Слайд 47Исследование с несколькими НП
Эффект одной независимой переменной в сложном (факторном) эксперименте
Он показывает, имеется ли эффект от воздействия данного отдельно взятого фактора.
Слайд 48Исследование с несколькими НП
Взаимодействие − это количественный результат, обусловленный соотношением между
Слайд 49Исследование с несколькими НП
Взаимодействие показывает, зависит ли величина воздействия фактора от
Слайд 50Исследование с несколькими НП
Нельзя интерпретировать результаты исследования, не принимая во внимание
Слайд 51Исследование с несколькими НП
Пример.
Психолог провел тренинг развития эмпатии для группы студентов,
Слайд 52Исследование с несколькими НП
В этом исследовании были выбраны две независимые переменные:
пол испытуемых (имеет два уровня − юноши и девушки) и
условия измерения эмпатии (имеет два уровня − до тренинга и после тренинга).
Зависимой переменной являлся уровень эмпатии (чем больше балл, набранный по некоторому тесту, тем больше уровень эмпатии).
Слайд 55Исследование с несколькими НП
Главные эффекты статистически независимы от эффектов взаимодействия, поэтому
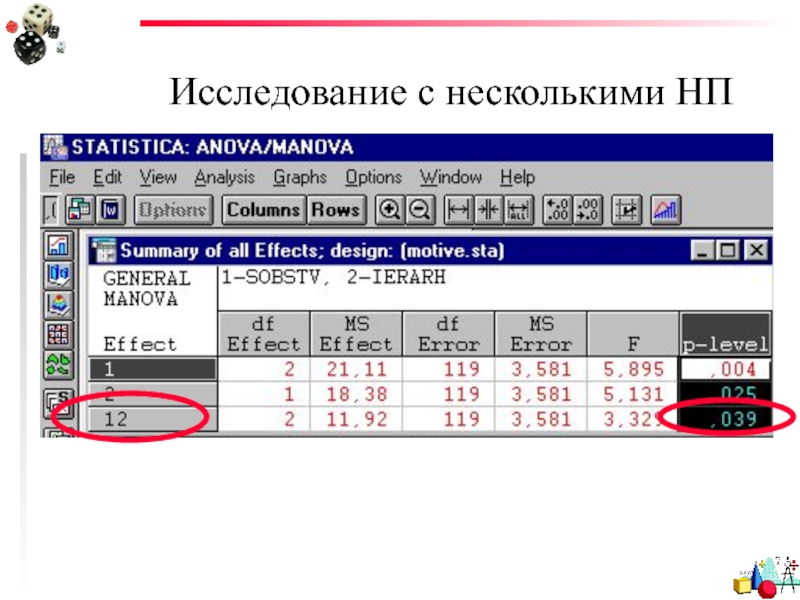
Слайд 56Исследование с несколькими НП
Для оценки значимости главных эффектор и значимости взаимодействия
Этот метод не имеет непараметрических аналогов – его нельзя заменить другими статистическими методами.
Слайд 58 Стой, Подумай, Примени
Исследователь провел эксперимент, чтобы определить
Слайд 59 Стой, Подумай, Примени
Исследователь собрал следующие данные о
Слайд 60 Стой, Подумай, Примени
Студент-психолог измерил тревожность в двух
Слайд 61 Стой, Подумай, Примени
Студент для курсового проекта проверяет,
Слайд 62 Стой, Подумай, Примени
Школьный психолог проверяет гипотезу о
Слайд 63 Стой, Подумай, Примени
Студент-дипломник решил посмотреть, как изменяется
Слайд 64 Стой, Подумай, Примени
Исследователь интересуется, зависит ли креативность
Слайд 65 Стой, Подумай, Примени
Студент Недотепкин для курсового проекта
Слайд 66 Стой, Подумай, Примени
В некотором эксперименте одной группе
Слайд 67 Стой, Подумай, Примени
Изучались способности к различным математическим
Слайд 68 Стой, Подумай, Примени
Три группы дошкольников участвуют в
Слайд 69Самостоятельная работа
К практическому занятию по ДА надо прочитать:
Высоков И.Е. Базовые
Слайд 71Многомерный ДА
Используется тогда, когда мы хотим проанализировать влияние НП сразу на
Часто называется MANOVA
Multivariate Analysis of Variance