- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пространство в современной физике презентация
Содержание
- 1. Пространство в современной физике
- 2. Пространство Одна из форм (наряду со временем)
- 3. Пространство в современной физике В современной физике используется математическая трактовка
- 4. Линейная алгебра: поле Поле – множество элементов
- 5. Линейная алгебра: поле Коммутативность: Ассоциативность:
- 6. Примеры полей Рациональные, вещественные числа Не являются
- 7. Векторное пространство Пространство над полем P
- 8. Векторное пространство Элемент пространства – вектор Вектор
- 9. Размерность пространства Рассмотрим линейную комбинацию:
- 10. Евклидово пространство Пространство, свойства которого изучаются в
- 11. Евклидово пространство: скалярное произведенье Рассмотрим:
- 12. Евклидово пространство Наше пространство – трехмерное евклидово пространство
- 13. Аксиомы Евклида 5 постулатов, на которых строится
- 14. Фазовое пространство Рассмотрим систему из N молекул.
- 15. Пространство Минковского Четырехмерное пространство. Помимо пространственных координат
- 16. Пространство Минковского Пространство Минковского можно сделать евклидовым, введя евклидову норму, но, зачастую, это неудобно
- 17. Пятый постулат Евклида Через точку, не лежащую
- 18. Геометрия Лобачевского Через точку, не лежащую на
- 19. Геометрия Лобачевского Лобачевскому удалось на основе своей
- 20. Выводы Понятие пространства в физике – это
- 21. Список литературы Ильин В. А., Позняк Э.Г.
Пространство Одна из форм (наряду со временем) существования бесконечно развивающейся материи… Литер.: Ожегов, Шведова «Толковый словарь русского языка» БСЭ статья «Пространство и время» Множество объектов, между которыми установлены
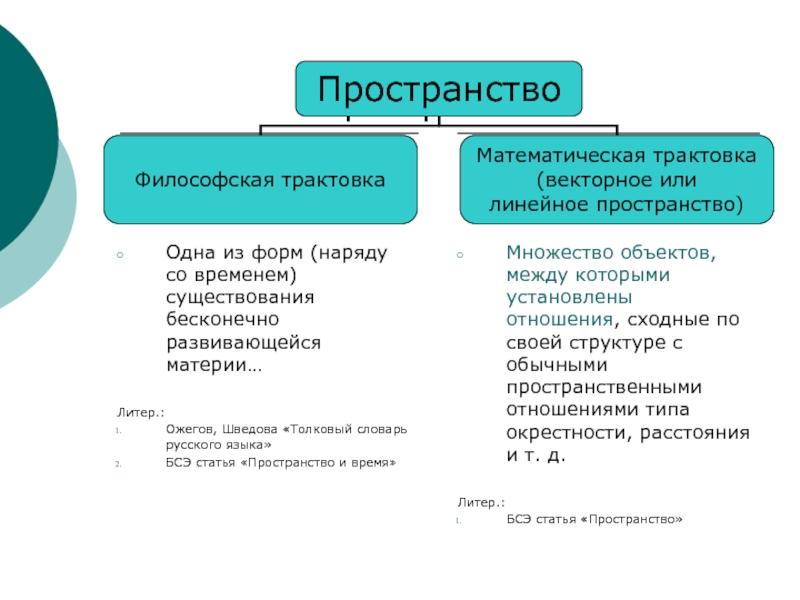
Слайд 2Пространство
Одна из форм (наряду со временем) существования бесконечно развивающейся материи…
Литер.:
Ожегов,
Шведова «Толковый словарь русского языка»
БСЭ статья «Пространство и время»
БСЭ статья «Пространство и время»
Множество объектов, между которыми установлены отношения, сходные по своей структуре с обычными пространственными отношениями типа окрестности, расстояния и т. д.
Литер.:
БСЭ статья «Пространство»
Слайд 4Линейная алгебра: поле
Поле – множество элементов с введенными на нем операциями
«+» и «*»; при этом операции «+» и «*» должны обладать определенным набором свойств
Слайд 5Линейная алгебра: поле
Коммутативность:
Ассоциативность:
Наличие нейтрального и обратного элемента:
Дистрибутивность:
Слайд 6Примеры полей
Рациональные, вещественные числа
Не являются полями: целые числа, натуральные числа
Будем говорить
о поле вещественных чисел
Слайд 7Векторное пространство
Пространство над полем P – это множество элементов, на
котором введены операции сложения и умножения на скаляр, обладающие определенными свойствами
Скаляр – элемент поля P
Скаляр – элемент поля P
Слайд 8Векторное пространство
Элемент пространства – вектор
Вектор задается координатами:
Радиус-вектор – вектор, начало которого
лежит в начале координат
Координатами точки называются координаты ее радиус-вектора
Координатами точки называются координаты ее радиус-вектора
Слайд 9Размерность пространства
Рассмотрим линейную комбинацию:
Где αn – ненулевые скаляры, а xn
– произвольные векторы.
Попытаемся подобрать скаляры так, чтобы л. к. обратилась в нуль. Размерность пространства - максимальное число векторов, для которых этого сделать не удастся. А оставшийся набор векторов называется базисом
Можно показать, что размерность пространство совпадает с числом координат векторов
Вещественное пространство размерности n обозначается Rn
Попытаемся подобрать скаляры так, чтобы л. к. обратилась в нуль. Размерность пространства - максимальное число векторов, для которых этого сделать не удастся. А оставшийся набор векторов называется базисом
Можно показать, что размерность пространство совпадает с числом координат векторов
Вещественное пространство размерности n обозначается Rn
Слайд 10Евклидово пространство
Пространство, свойства которого изучаются в евклидовой геометрии. В более широком
понимании Е. п. называют n-мерное векторное пространство, в котором определено скалярное произведенье
Литер.:
БСЭ статья «Евклидово пространство»
Литер.:
БСЭ статья «Евклидово пространство»
Слайд 11Евклидово пространство: скалярное произведенье
Рассмотрим:
Где x, y принадлежат пространству R2, а x1,
x2, y1, y2 – полю R.
Введем скалярное произведенье:
Причем λ принадлежит полю P.
Скалярное произведенье порождает норму:
Введем скалярное произведенье:
Причем λ принадлежит полю P.
Скалярное произведенье порождает норму:
Слайд 13Аксиомы Евклида
5 постулатов, на которых строится геометрия евклидового пространства
Сформулированы Евклидом для
R2
Гильберт уточнил аксиоматику и распространил ее на случай R3
Гильберт уточнил аксиоматику и распространил ее на случай R3
Слайд 14Фазовое пространство
Рассмотрим систему из N молекул. В каждый момент времени у
каждой i-той молекулы определен вектор скорости:
и радиус-вектор (вектор-положение):
В каждый момент времени состояние системы описывается точкой в 6N-мерном фазовом пространстве:
и радиус-вектор (вектор-положение):
В каждый момент времени состояние системы описывается точкой в 6N-мерном фазовом пространстве:
Слайд 15Пространство Минковского
Четырехмерное пространство. Помимо пространственных координат вводится временная ct
Не является Евклидовым,
так как определение нормы отлично от данного выше
Квадрат нормы в пространстве Минковского:
Квадрат нормы в пространстве Минковского:
Слайд 16Пространство Минковского
Пространство Минковского можно сделать евклидовым, введя евклидову норму, но, зачастую,
это неудобно
Слайд 17Пятый постулат Евклида
Через точку, не лежащую на данной прямой, проходит только
одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её
Слайд 18Геометрия Лобачевского
Через точку, не лежащую на данной прямой, проходят по крайней
мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её
Слайд 19Геометрия Лобачевского
Лобачевскому удалось на основе своей аксиоматики построить полную и непротиворечивую
геометрию
Геометрия Лобачевского находит применение в специальной и общей теории относительности
Геометрия Лобачевского находит применение в специальной и общей теории относительности
Слайд 20Выводы
Понятие пространства в физике – это абсолютно строгая математическая модель
Евклидово пространство
– частный случай этой модели
В большинстве случаев удобно полагать, что мы живем в трехмерном Евклидовом пространстве
Часто для расчета физических процессов приходится прибегать к использованию евклидовых пространств с большим числом измерений
В большинстве случаев удобно полагать, что мы живем в трехмерном Евклидовом пространстве
Часто для расчета физических процессов приходится прибегать к использованию евклидовых пространств с большим числом измерений
Слайд 21Список литературы
Ильин В. А., Позняк Э.Г. «Линейная алгебра». Изд.: Москва Наука
1999 г.
Гельфанд И. М. «Лекции по линейной алгебре». Изд.: МЦНМО 1998 г.
Апатенок Р. Ф. «Элементы линейной алгебры». Изд.: Минск «Высшая школа» 1977 г.
Н. В. Ефимов, Э. Р. Розендорн. «Линейная алгебра и многомерная геометрия». 1970 г.
Манин Ю. И., Кострикин А. И. «Линейная алгебра и геометрия». 1980 г.
Гельфанд И. М. «Лекции по линейной алгебре». Изд.: МЦНМО 1998 г.
Апатенок Р. Ф. «Элементы линейной алгебры». Изд.: Минск «Высшая школа» 1977 г.
Н. В. Ефимов, Э. Р. Розендорн. «Линейная алгебра и многомерная геометрия». 1970 г.
Манин Ю. И., Кострикин А. И. «Линейная алгебра и геометрия». 1980 г.
