- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Промежутки возрастания, убывания, знакопостоянства и нули функций презентация
Содержание
- 1. Промежутки возрастания, убывания, знакопостоянства и нули функций
- 2. В о з р а
- 3. х₁ < x₂
- 4. Значения аргумента, при которых
- 5. 1 1 0 у х у
- 6. Как найти нули функции, заданной формулой? Найти
- 7. При каких значениях х значения
- 8. Какова область определения функции? Какова
- 9. При каких х значения функции
- 10. Нет На каком из рисунков функция,
- 11. y На каком
- 12. 1 4 3 3 Функция
- 13. Функция у = f (x) определена графиком.
- 14. Функция у = f(x) определена графиком. Укажите
Слайд 3
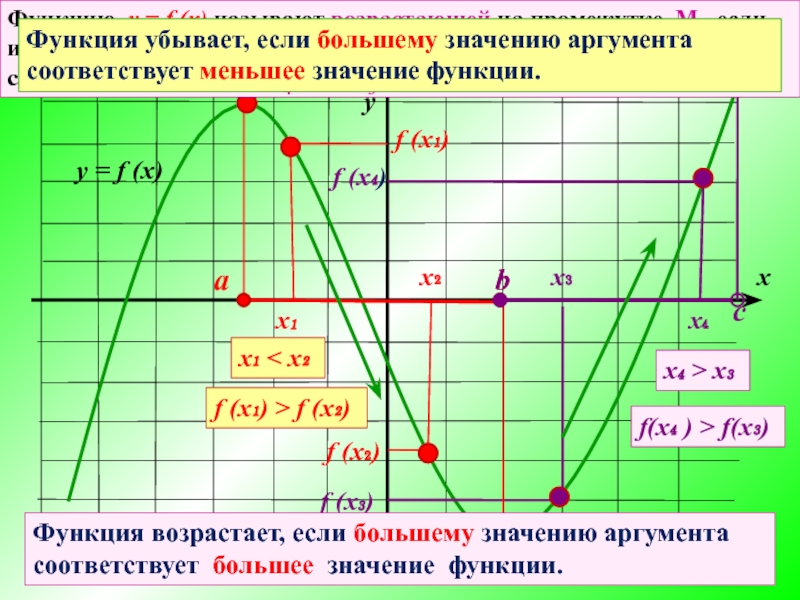
х₁ < x₂
х₂
х₁
f (x₁)
f (x₂)
f (x₁) > f (x₂)
х₃
х₄
f (x₄)
f (x₃)
х₄
f(х₄ ) > f(x₃)
a
b
c
b
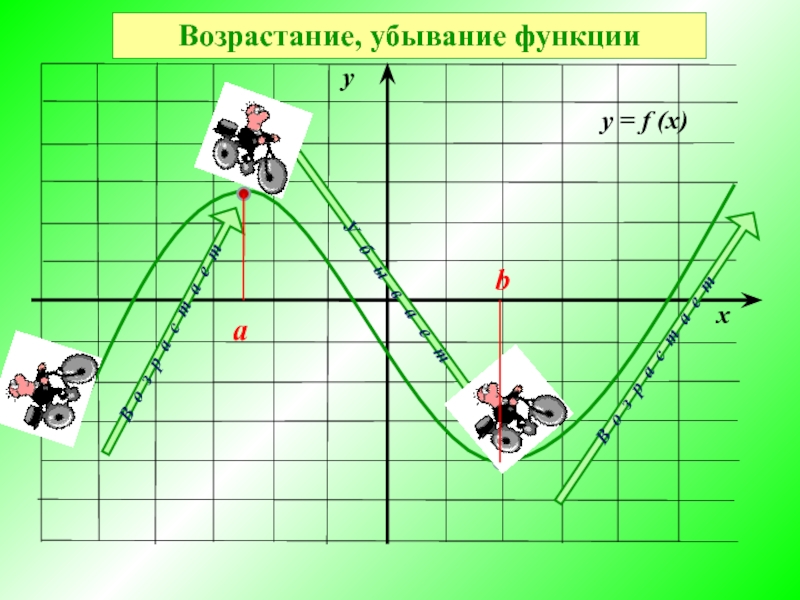
Функцию y = f (x) называют убывающей на промежутке N, если из неравенства x₁ < x₂, где x₁ и x₂ - любые точки из промежутка N, следует неравенство f (x₁) > f (x₂)
Функцию y = f (x) называют возрастающей на промежутке M, если из неравенства x 3 < x 4, где x 3 и x 4 - любые точки из промежутка M, следует неравенство f (x 4 ) > f (x 3 ).
Функция возрастает, если большему значению аргумента соответствует большее значение функции.
Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
y = f (x)
Слайд 4
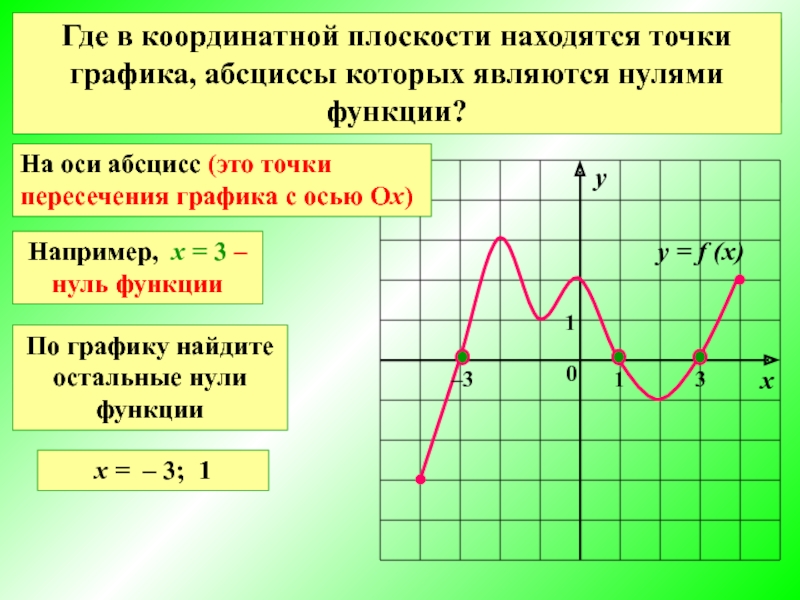
Значения аргумента, при которых значения функции равны нулю, называют нулями функции
Где
На оси абсцисс (это точки пересечения графика с осью Ох)
Например, х = 3 ‒ нуль функции
3
По графику найдите остальные нули функции
‒3
х = ‒ 3; 1
Слайд 6Как найти нули функции, заданной формулой?
Найти нули функции
По смыслу задания у
х ‒ 6 = 0 или х + 6 = 0, тогда
Найдите нули функций
х = 16
Слайд 7
При каких значениях х значения
функции отрицательны?
Ответ:
При каких значениях х значения
функции положительны?
(-1;0); (0;1)
1
○
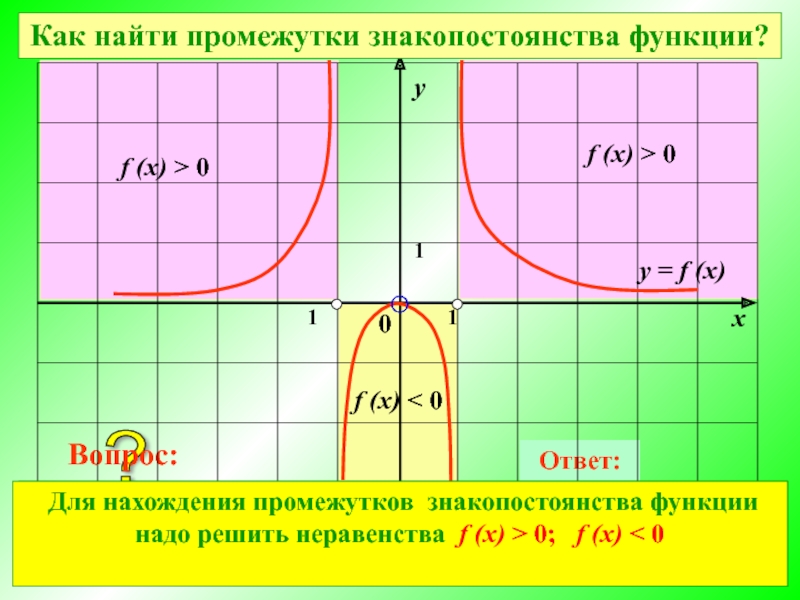
f (x) < 0
f (x) > 0
f (x) > 0
Промежутки знакопостоянства функции
Промежутки знакопостоянства функции ‒ это все значения аргумента х, при которых значения функции положительны (у > 0) или отрицательны (у < 0)
Как найти промежутки знакопостоянства функции?
Для нахождения промежутков знакопостоянства функции надо решить неравенства f (x) > 0; f (x) < 0
Слайд 8
Какова область
определения функции?
Какова область
значений функции.
[-5;5]
[-2;4]
Назовите нули
функции.
-4;-2;0;2;4
Назовите промежутки
убывания
[-3;1], [1;2]
Назовите промежутки
возрастания функции.
[-5;-3], [-1;3], [3;5]
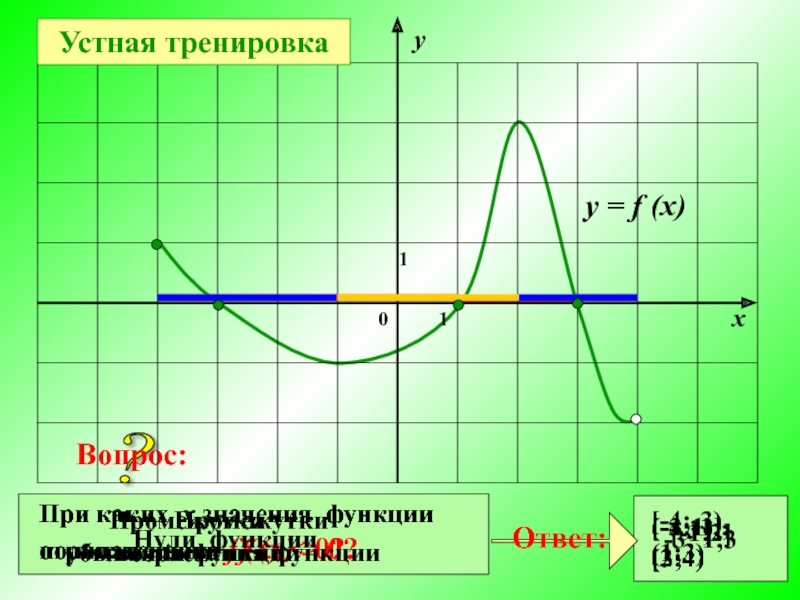
Устная тренировка
Слайд 9
При каких х значения функции
положительны f (x) > 0?
При каких
[-4;-3),
(1;3)
(-3;1),
(3;4)
Нули функции
-3; 1;3
Промежутки
убывания функции
[-4;-1],
[2;4)
Промежутки
возрастания функции
[-1;2]
Устная тренировка
Слайд 10Нет
На каком из рисунков функция, заданная графиком, убывает на промежутке
3
4
2
1
Нет
Отлично
Проверка (4)
Нет
x
y
0
1
0
1
0
1
0
1
x
x
x
y
y
y
Слайд 11y
На каком из рисунков функция, заданная графиком,
возрастает на промежутке [0; 3]?
1
4
2
3
Нет
Отлично
Проверка (4)
Нет
Нет
x
0
1
x
0
1
x
0
1
x
0
1
y
y
y
Слайд 121
4
3
3
Функция у = f (x) задана на промежутке [-7; 8].
Укажите длину промежутка возрастания этой функции.
Проверка
y = f (x)
1 2 3 4 5 6 7 8
-7 -6 -5 -4 -3 -2 -1
y
x
5
4
3
2
1
-1
-2
-3
-4
2
11
8
Нет
Нет
Нет
Отлично
5
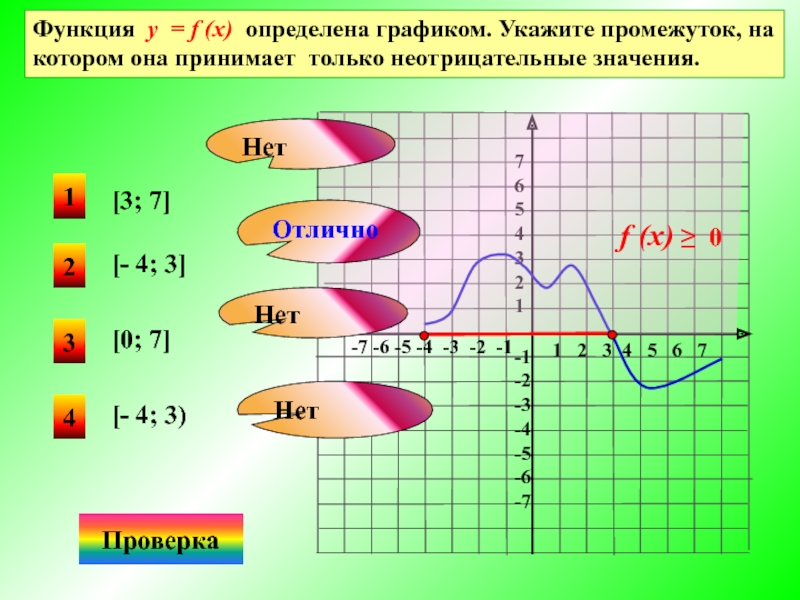
Слайд 13Функция у = f (x) определена графиком. Укажите промежуток, на котором
Проверка
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
[- 4; 3]
2
1
3
4
Нет
Нет
Отлично
Нет
[3; 7]
[0; 7]
[- 4; 3)
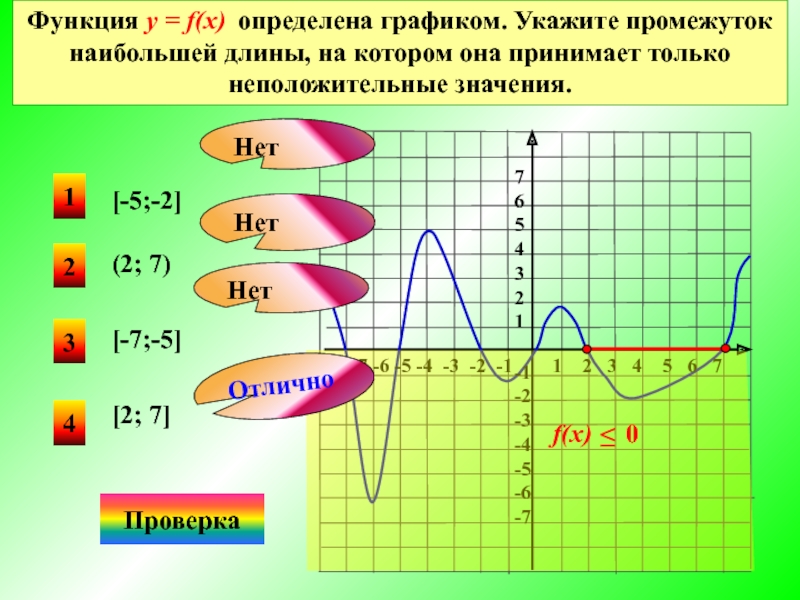
Слайд 14Функция у = f(x) определена графиком. Укажите промежуток наибольшей длины, на
Проверка
1 2 3 4 5 6 7
-7 -6 -5 -4 -3 -2 -1
7
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-7
(2; 7)
4
1
3
2
Нет
Нет
Отлично
Нет
[-5;-2]
[-7;-5]
[2; 7]



![Какова область определения функции?Какова область значений функции.[-5;5][-2;4]Назовите нули функции.-4;-2;0;2;4Назовите промежутки убывания функции[-3;1], [1;2]Назовите промежутки возрастания](/img/tmb/5/493626/e0a4516c374e6fde3eab06c4e7d521eb-800x.jpg)
![Нет На каком из рисунков функция, заданная графиком, убывает на промежутке [0; 3]?3421Нет Отлично Проверка](/img/tmb/5/493626/dd532c86d13a5d95e5785ffbbf5c77cd-800x.jpg)
![y На каком из рисунков функция, заданная графиком, возрастает на промежутке [0; 3]?](/img/tmb/5/493626/983aa9f7be4ae37aae59efb8eb78c1e8-800x.jpg)
![1433Функция у = f (x) задана на промежутке [-7; 8]. Укажите длину промежутка возрастания этой](/img/tmb/5/493626/50db21404bf09f758b4bde8484dcaa83-800x.jpg)