- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пример решения транспортной задачи (открытая модель) презентация
Содержание
- 1. Пример решения транспортной задачи (открытая модель)
- 2. Задача Выпуск продукции трех заводов A1, A2,
- 3. Решение: Так как a1+a2+a3 = 260+240+300 =
- 4. Решение задачи методом наименьшей стоимости 240 3
- 5. Опорное решение задачи Проверим опорный план X1 на оптимальность
- 6. Составим систему уравнений для заполненных ячеек: u1
- 7. Проверим второе условие теоремы для незаполненных строк
- 8. Оптимальное решение: Zmin = 110*3+150*4+240*2+190*4+50*3+60*6+ +10*0+40*0 = 2680
- 9. Используемая литература: Борзунова Т.Л., Барыкин М.П. ,
Слайд 2Задача
Выпуск продукции трех заводов A1, A2, A3 составляет 260, 240, 300
Известно:
1) продукция завода A1 не требуется пункту B4;
2) с завода A3 потребителю B2 должно быть доставлено груза не более 50 т.
Тарифы перевозок сij (в ден/ед.) из Ai в Bj приведены в матрице:
Составить оптимальный план перевозок груза.
Слайд 3Решение:
Так как a1+a2+a3 = 260+240+300 = 800,
т.е. (b1+b2+b3+b4)-(a1+a2+a3) = 50, то введем фиктивного поставщика A4 с запасами a4=50 и нулевыми тарифами.
1) В клетку A1B4 запишем число M (блокируем).
Получили закрытую модель транспортной задачи.
Учтем условия:
2) В столбце B2 запишем потребности b2=50, остальные b2*=150 заносим в дополнительный столбец B2*.
Все тарифы, как в B2, но в A3B2* ставим число M.
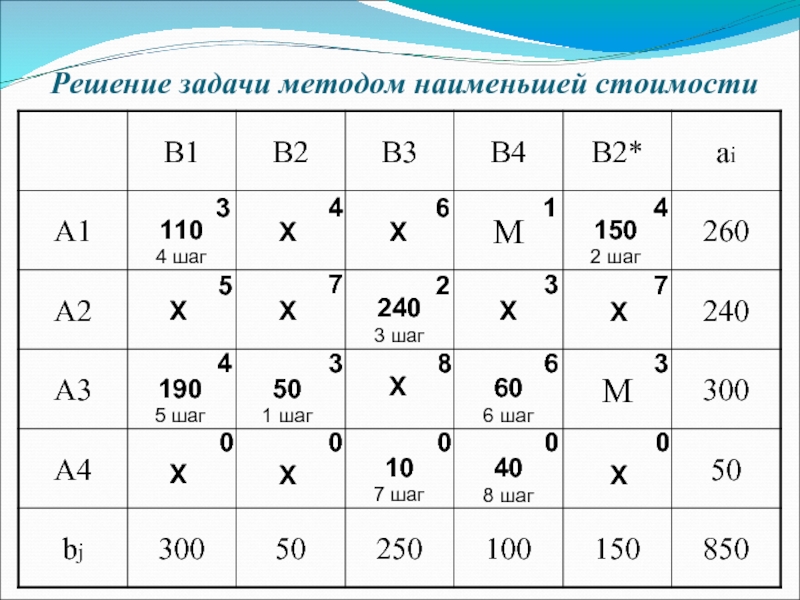
Слайд 4Решение задачи методом наименьшей стоимости
240
3 шаг
3
4
6
1
4
5
7
2
3
7
4
3
8
6
3
0
0
0
0
0
Х
Х
Х
Х
50
1 шаг
40
8 шаг
Х
Х
150
2 шаг
Х
110
4 шаг
Х
190
5 шаг
Х
60
6
Х
10
7 шаг
Слайд 6Составим систему уравнений
для заполненных ячеек:
u1 + v1 = 3
u1 + v2*
u2 + v3 = 2
u3 + v1 = 4
u3 + v2 = 3
u3 + v4 = 6
u4 + v3 = 0
u4 + v4 = 0
Пусть u1 = 0, тогда:
Так как v1 = 3, то
v1 = 3
v2*= 4
u3 = 1
Так как u3 = 1, то
v2 = 2
Так как u3 = 1, то
v4 = 5
Так как v4 = 5, то
u4 = −5
Итак, u1 = 0, u2 = −3, u3 = 1, u4 = −5,
v1 = 3, v2 = 2, v2*= 4, v3 = 5, v4 = 5
Так как u4 = −5, то
v3 = 5
Так как v3 = 5, то
u2 = −3
Слайд 7Проверим второе условие теоремы
для незаполненных строк
u1 + v2* = 4 ≤
Но ячейка A1B4 заблокирована, следовательно, план X1 оптимальный
u1 + v3 = 5 ≤ C13 = 6 +
u1 + v4 = 5 > C14 = 1 (−4)
u2 + v1 = 0 ≤ C21 = 5 +
u2 + v2 = −1 ≤ C22 = 7 +
u2 + v4 = 2 ≤ C24 = 3 +
u1 = 0, u2 = −3, u3 = 1, u4 = −5,
v1 = 3, v2 = 2, v2*= 4, v3 = 5, v4 = 5
u3 + v3 = 6 ≤ C33 = 8 +
u4 + v1 = −2 ≤ C41 = 0 +
u4 + v2 = −3 ≤ C42 = 0 +
Слайд 9Используемая литература:
Борзунова Т.Л., Барыкин М.П. , Данилов Е.А. Соловьева О.Ю. -
Конюховский П.В. Математические методы исследования операций в экономике – СПб: Питер, 2000.