- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение производной к исследованию функций презентация
Содержание
- 1. Применение производной к исследованию функций
- 2. Великий французский математик Пьер Ферма в 1629
- 3. Как родилась производная Тем не менее,
- 4. Как родилась производная Очень многие великие ученые
- 5. Исследование функции: D(f) E(f) Пересечение с координатными
- 6. Четность, нечетность функций Периодичность Нули функции Промежутки знакопостоянства Монотонность функции Повторение далее
- 7. Четность функций Определение: Функция y = f(x)
- 8. f(-x0) O y
- 9. Определение: Функция y = f(x) называется периодической,
- 10. х1, х2, х3 – нули функции
- 11. Промежутки знакопостоянства Определение: Числовые промежутки,
- 12. Монотонность функции Определение: Функцию называют монотонно возрастающей,
- 13. Если производная функции в каждой точке некоторого
- 14. f’(x)>0 f’(x)
- 15. Внутренние точки области определения, в которых производная
- 16. критические точки Достаточный признак возрастания
- 17. ЭКСТРЕМУМ ФУНКЦИИ Точка х0 называется точкой
- 18. Точка х1 называется точкой
- 19. max min max Точки экстремумов хі
- 20. Обратите внимание!!! Что происходит с производной при
Слайд 2Великий французский математик Пьер Ферма в 1629 году научился находить касательные
Как родилась производная
Ферма далеко продвинулся в применении дифференциальных методов, он использовал их не только для проведения касательных, но, к примеру, для нахождения максимумов, вычисления площадей. Однако ни Ферма, ни Декарт не сумели свести полученные научные выводы и результаты в единую систему.
В 1638 году Ферма поделился этим открытием со своим земляком Рене Декартом, который также занимался этой проблемой и нашел свой метод построения касательных к алгебраическим кривым.
Слайд 3Как родилась производная
Тем не менее, выдвинутые идеи не пропали впустую.
Многие
Исаак
Ньютон
(1642-1727)
Вильгельм
Лейбниц
(1646-1716)
Слайд 4Как родилась производная
Очень многие великие ученые внесли свой вклад в зарождение
Якоб
Бернулли
(1654-1705)
Джеймс
Грегори
(1638-1675)
Гийом
Франсуа
Лопиталь
(1661-1704)
Жозеф
Луи Лагранж
(1736-1813)
Леонард
Эйлер
(1707-1783)
Карл
Фридрих
Гаусс
(1777-1855)
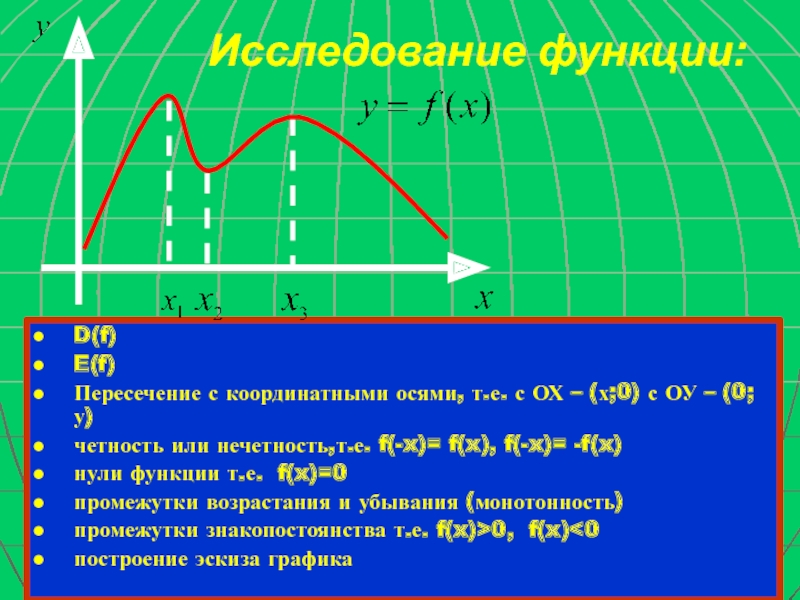
Слайд 5Исследование функции:
D(f)
E(f)
Пересечение с координатными осями, т.е. с ОХ – (х;0) с
четность или нечетность,т.е. f(-x)= f(x), f(-x)= -f(x)
нули функции т.е. f(x)=0
промежутки возрастания и убывания (монотонность)
промежутки знакопостоянства т.е. f(x)>0, f(x)<0
построение эскиза графика
Слайд 6Четность, нечетность функций
Периодичность
Нули функции
Промежутки знакопостоянства
Монотонность функции
Повторение
далее
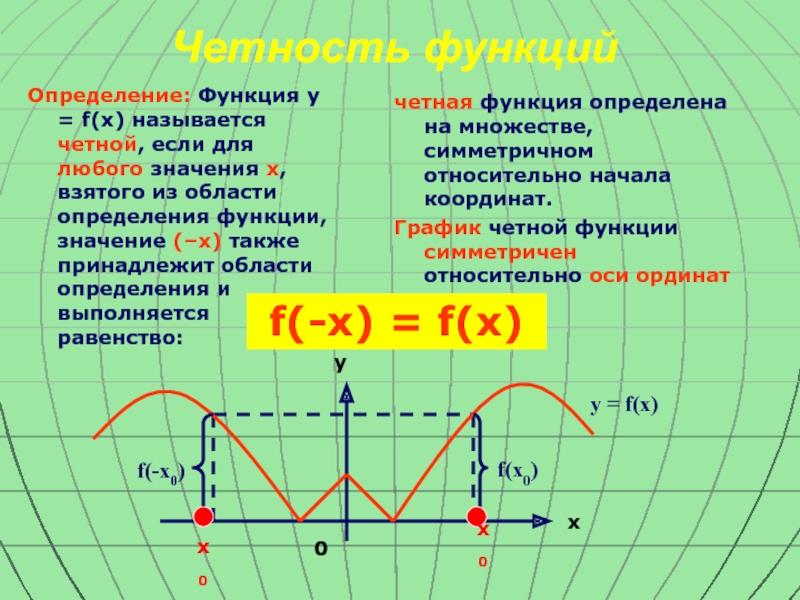
Слайд 7Четность функций
Определение: Функция y = f(x) называется четной, если для любого
четная функция определена на множестве, симметричном относительно начала координат.
График четной функции симметричен относительно оси ординат
у
х
0
f(-x) = f(x)
х0
- х0
Слайд 8
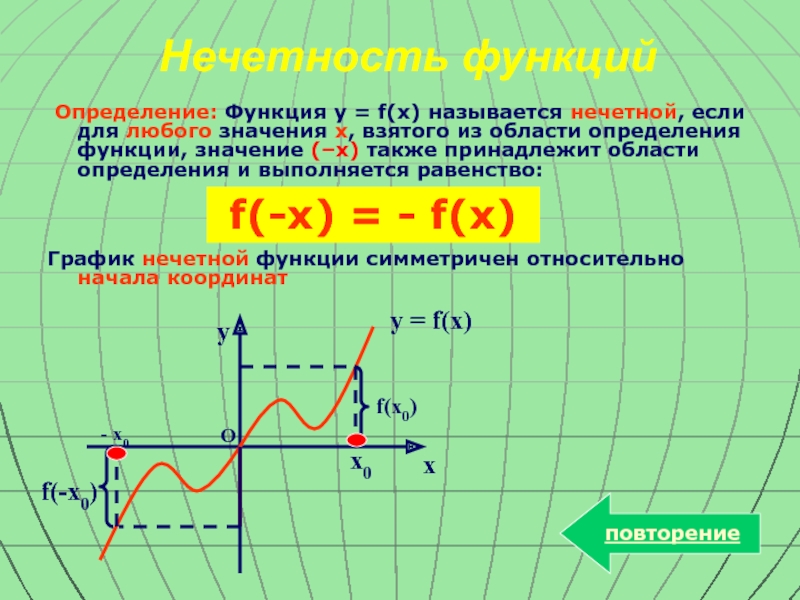
f(-x0)
O
y = f(x)
Нечетность функций
Определение: Функция y = f(x) называется
График нечетной функции симметричен относительно начала координат
повторение
f(-x) = - f(x)
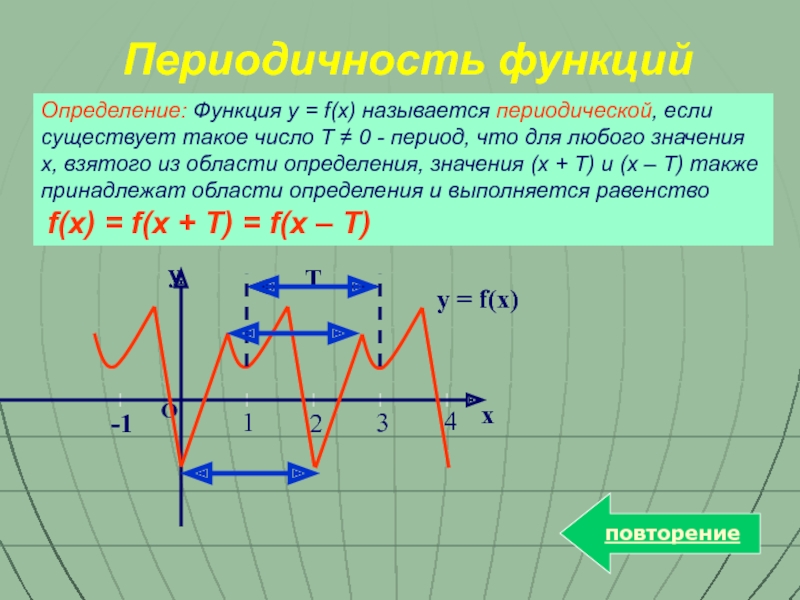
Слайд 9Определение: Функция y = f(x) называется периодической, если существует такое число
f(x) = f(x + T) = f(x – T)
y
1
2
4
3
-1
T
y = f(x)
Периодичность функций
повторение
Слайд 10
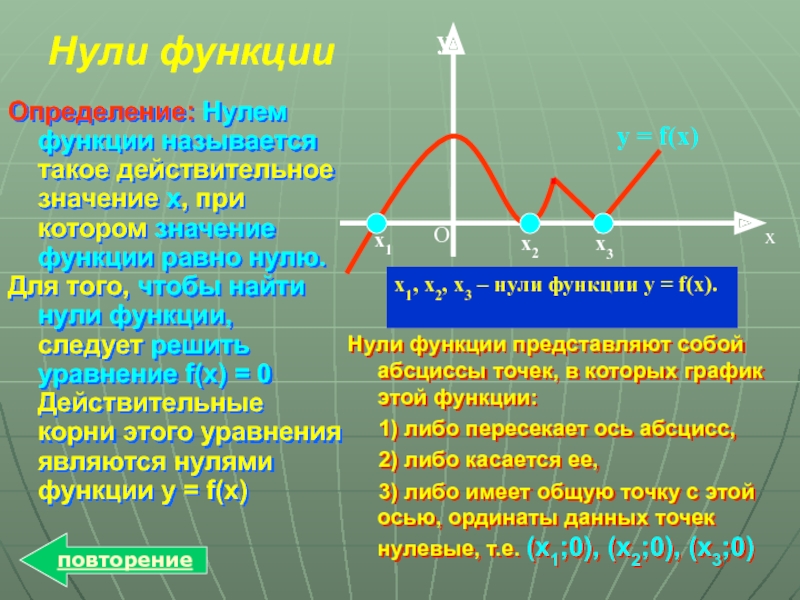
х1, х2, х3 – нули функции у = f(x).
Нули функции
Определение:
Для того, чтобы найти нули функции, следует решить уравнение f(x) = 0 Действительные корни этого уравнения являются нулями функции y = f(x)
Нули функции представляют собой абсциссы точек, в которых график этой функции:
1) либо пересекает ось абсцисс,
2) либо касается ее,
3) либо имеет общую точку с этой осью, ординаты данных точек нулевые, т.е. (х1;0), (х2;0), (х3;0)
повторение
Слайд 11
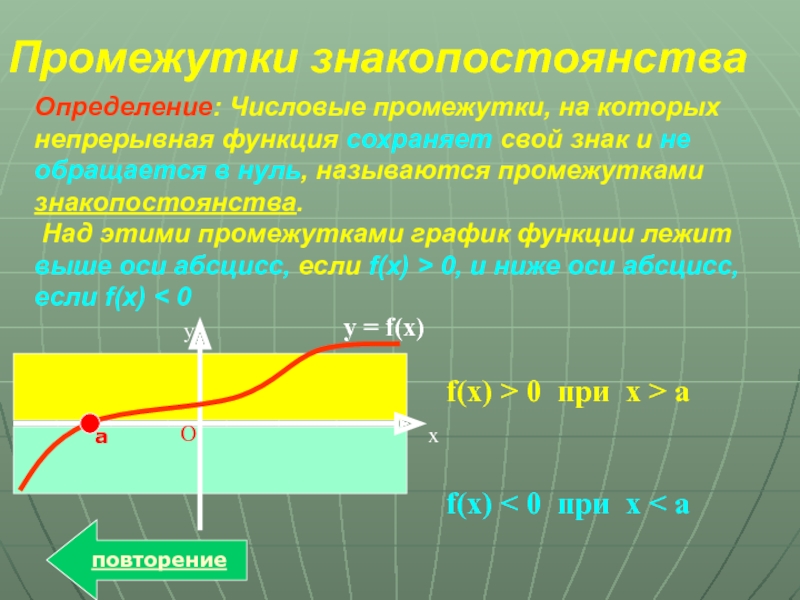
Промежутки знакопостоянства
Определение: Числовые промежутки, на которых непрерывная функция сохраняет свой знак
Над этими промежутками график функции лежит выше оси абсцисс, если f(x) > 0, и ниже оси абсцисс, если f(x) < 0
повторение
a
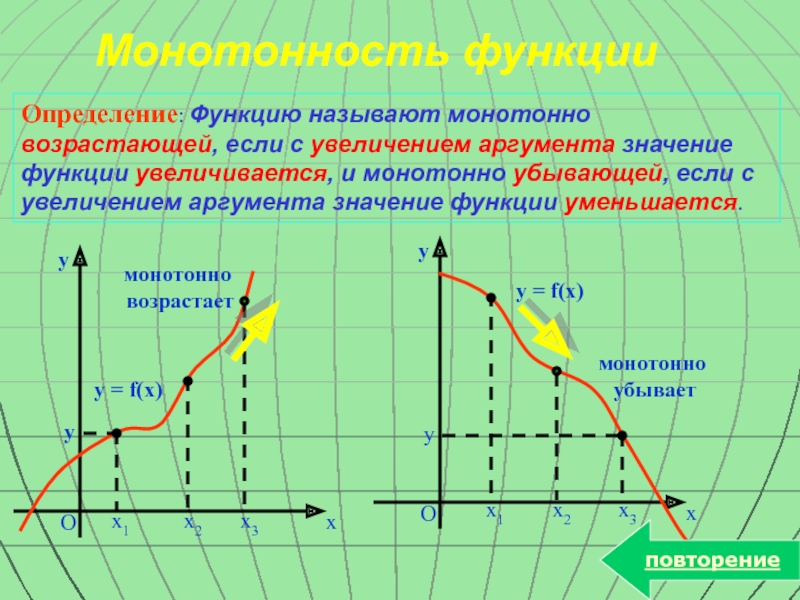
Слайд 12Монотонность функции
Определение: Функцию называют монотонно возрастающей, если с увеличением аргумента значение
y = f(x)
y = f(x)
монотонно
убывает
y
x3
x2
x1
повторение
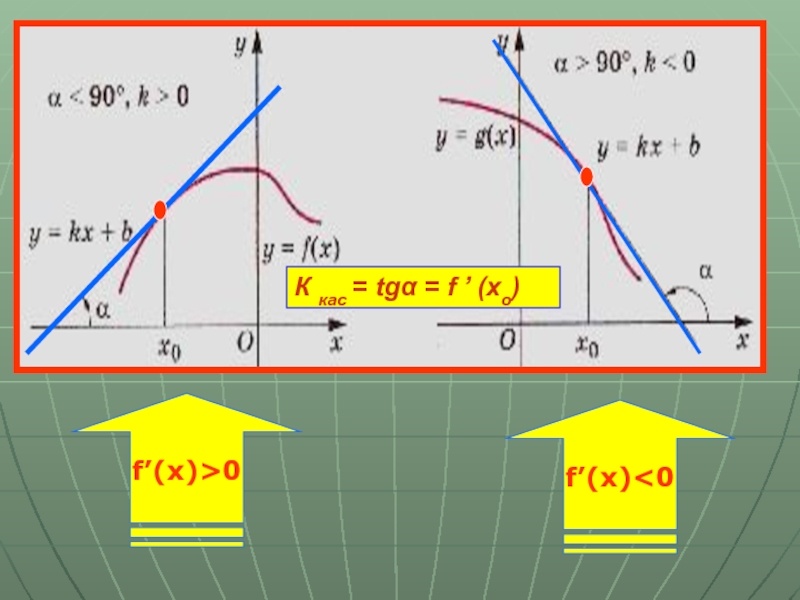
Слайд 13Если производная функции в каждой точке некоторого промежутка положительна, то функция
Если производная функции в каждой точке некоторого промежутка отрицательна, то функция на этом промежутке убывает, т.е.f’(x)<0, f(x)⭨
Если производная функции в каждой точке некоторого промежутка равна 0, то функция на этом промежутке постоянна
Связь производной с монотонностью функции
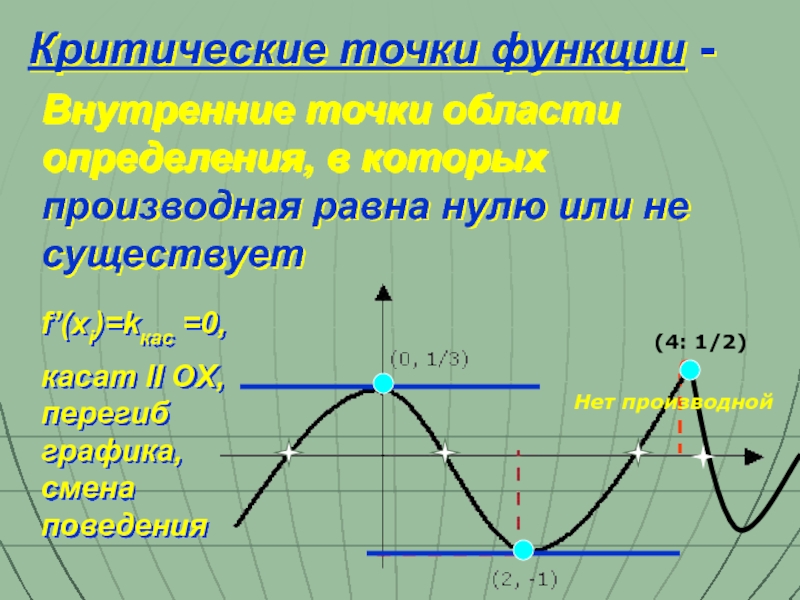
Слайд 15Внутренние точки области определения, в которых производная равна нулю или не
Критические точки функции -
(4: 1/2)
f’(xi)=kкас =0,
касат II OX, перегиб графика, смена поведения
Нет производной
Слайд 16
критические
точки
Достаточный признак возрастания или убывания функции
Пример: Найти промежутки возрастания и
Решение:
1) f ’(x)=(x3-3x2+2)’=3х2-6х=3х(х-2)
2)Находим критичекие точки: f’(x)=0, т.е. 3х(х-2)=0 при х=0 х=2
3) Исследуем знак производной методом интервалов
Ответ: f (x)⭧ на (-∞; 0)∪ (2;∞)
f (x)⭨ на (0;2)
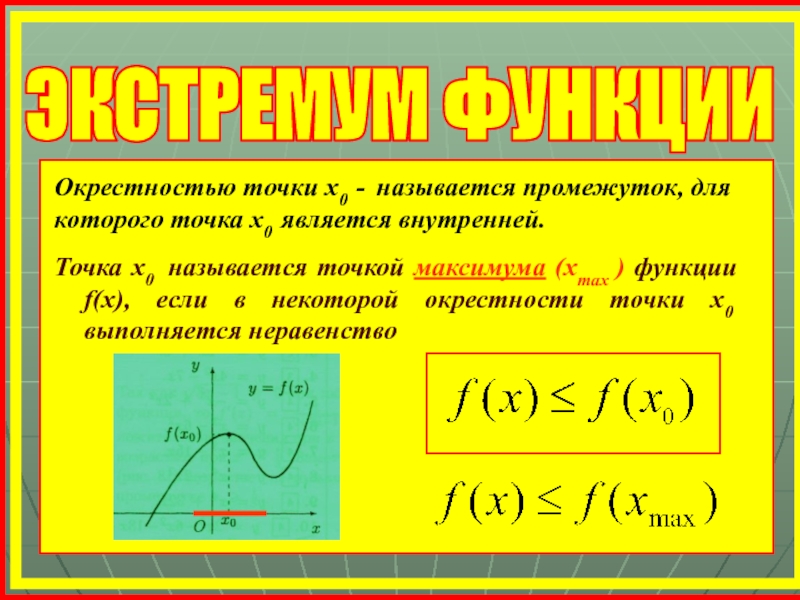
Слайд 17ЭКСТРЕМУМ ФУНКЦИИ
Точка х0 называется точкой максимума (xmax ) функции f(x), если
Окрестностью точки х0 - называется промежуток, для которого точка х0 является внутренней.
Слайд 18
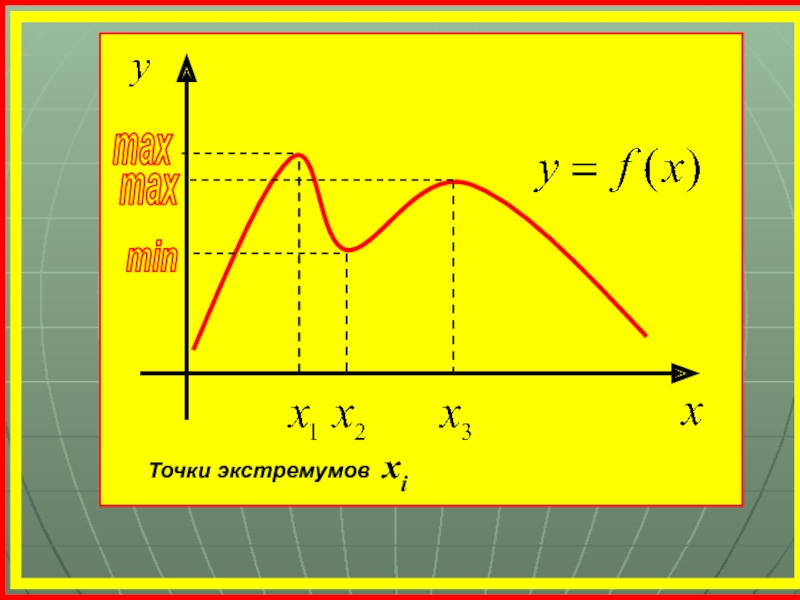
Точка х1 называется точкой минимума (xmin ) функции f(x),
Точки минимума и максимума называются
точками экстремума (крайние, конечные)
Значения функции в точках х0 и х1
называются соответственно
максимумом и минимумом функции (ymin и ymax)
Максимум и минимум функции называется
экстремумом функции
Слайд 20Обратите внимание!!!
Что происходит с производной при переходе через экстремальную точку?
Что происходит
удачи в изучении ))