- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение прогрессий в экономических расчетах презентация
Содержание
- 1. Применение прогрессий в экономических расчетах
- 2. Цель исследования: Рассмотреть примеры применения прогрессий при решении экономических задач (банковских расчетов).
- 3. Задачи исследования: Изучить литературу по теме исследования.
- 4. Объект исследования: арифметическая и геометрическая прогрессии.
- 5. Арифметическая прогрессия – числовая последовательность, в которой
- 6. Формулы суммы прогрессий. Арифметической прогрессии:
- 7. Представьте себе, что вы открыли в банке
- 8. В первом случае при n = 1
- 9. Математическая модель ситуации — конечная геометрическая прогрессия
- 10. Сравнительная таблица
- 11. Рассмотрим конкретный пример. Банк начисляет ежегодно
- 13. Моим родителям к концу июля 2015 года
- 14. Что делать? Открыть вклад на 5 месяцев
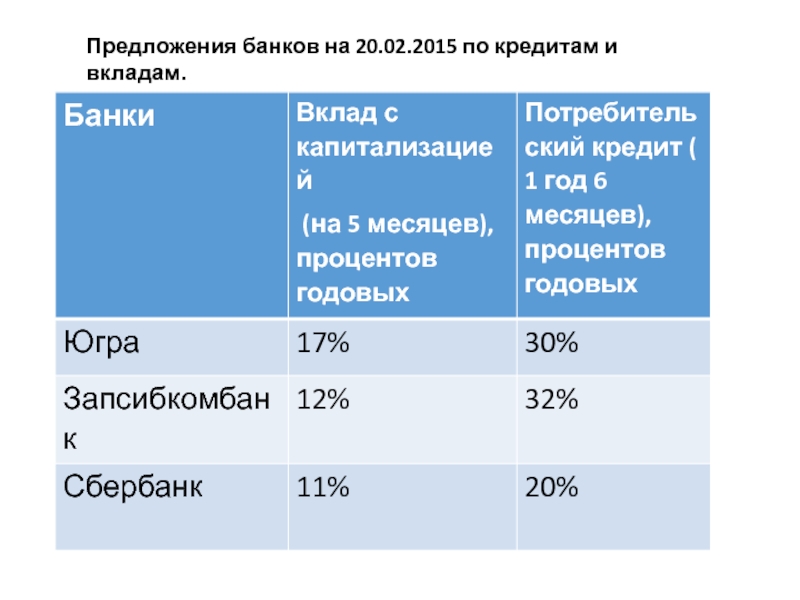
- 15. Предложения банков на 20.02.2015 по кредитам и вкладам.
- 17. В своей работе я рассмотрел основные формулы
- 18. Спасибо за внимание!
Слайд 2Цель исследования:
Рассмотреть примеры применения прогрессий при решении экономических задач (банковских расчетов).
Слайд 3Задачи исследования:
Изучить литературу по теме исследования.
Показать как и каким образом прогрессии
Рассмотреть задачу: как правильно выбрать банк, чтобы выгодно сделать вклад и взять кредит с наименьшей переплатой.
Слайд 4Объект исследования:
арифметическая и геометрическая прогрессии.
Предмет исследования:
практическое применение прогрессий в банковских расчетах.
Слайд 5Арифметическая прогрессия – числовая последовательность, в которой каждое последующее число, начиная
Имеет вид: a1, a1+d, a1+2d, a1+3d, … a1+(n-1)d, …
Геометрическая прогрессия — последовательность чисел, в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число.
Имеет вид: b1, b1q, b1q2, b1q3,… ,b1qn-1,…
Слайд 6Формулы суммы прогрессий.
Арифметической прогрессии:
Геометрической прогрессии:
Формула суммы бесконечной геометрической прогрессии
Слайд 7Представьте себе, что вы открыли в банке вклад в сумме P
Какой доход вы получите в том и другом случаях?
Слайд 8В первом случае при n = 1 вы получите (P+ i*a
t = 2 ваша итоговая сумма составит (P + 2*i*P)р., при t= 3
(P + 3*i*P )р. и т. д.
Математическая модель ситуации — конечная арифметическая прогрессия P, P + i*P , P + 2*i*P ,P + 4*i*P …, P + n*i*P .
Итак, при первой стратегии поведения за n лет вы получите:
P(1 + n*i)— это так называемая формула простых процентов.
Слайд 9Математическая модель ситуации — конечная геометрическая прогрессия а, P(1 + i*P
Итак, при второй стратегии поведения за N лет вы получите
P(1 + i )^n руб.— это так называемая формула сложных процентов.
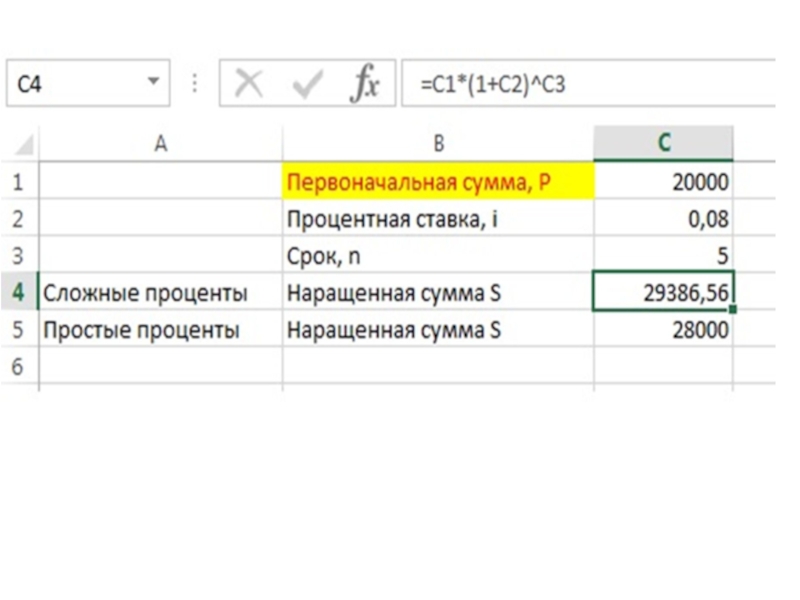
Слайд 11Рассмотрим конкретный пример.
Банк начисляет ежегодно 8% (сложных процентов). Клиент положил
Сравнить полученную сумму с наращенной суммой, которая могла быть получена в случае выплаты простых процентов.
Слайд 13Моим родителям к концу июля 2015 года необходима сумма в размере
Задача:
Слайд 14Что делать?
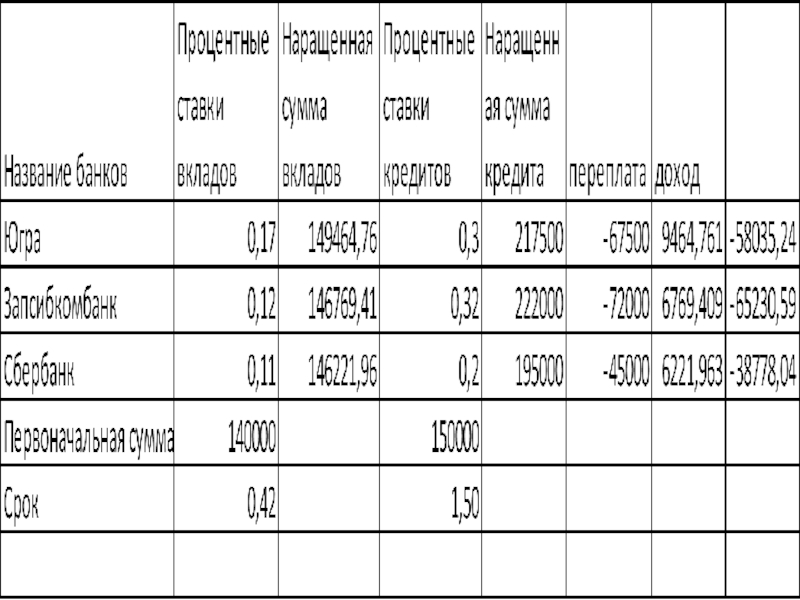
Открыть вклад на 5 месяцев (сумма 140 000 руб.).
Взять кредит
Слайд 17В своей работе я рассмотрел основные формулы арифметической и геометрической прогрессий.
1. В
2. Одним из самых выгодных банков для вкладов и кредитов одновременно является Сбербанк.
Заключение