ОГБОУ СПО «Ангарский медицинский колледж»
Черных А.А., преподаватель математики и информатики
2015
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение математических методов для решения содержательных задач из различных областей науки и практики презентация
Содержание
- 1. Применение математических методов для решения содержательных задач из различных областей науки и практики
- 2. Содержание: Задание1. Несложная арифметическая текстовая
- 3. Задание 1. Для ремонта квартиры требуется
- 4. Задание 1. Задача 2. Ответ:
- 5. Задание 1. Задача 3.
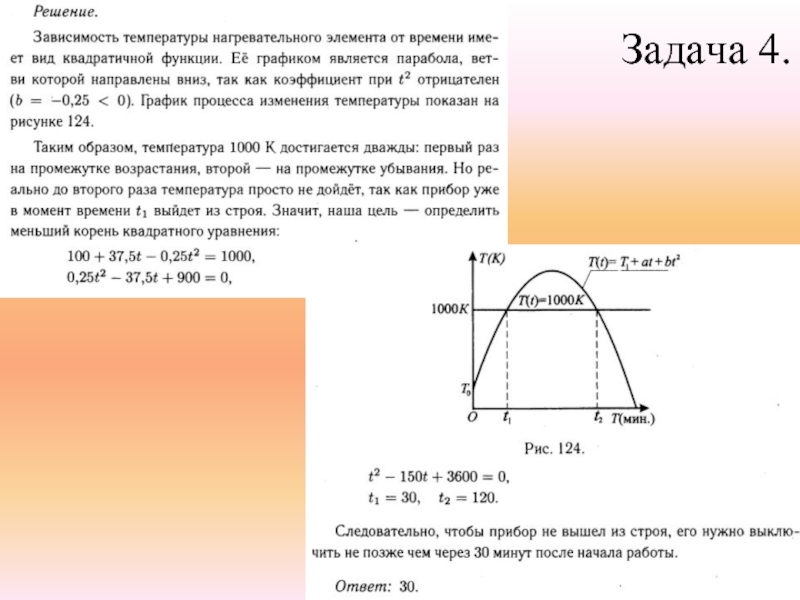
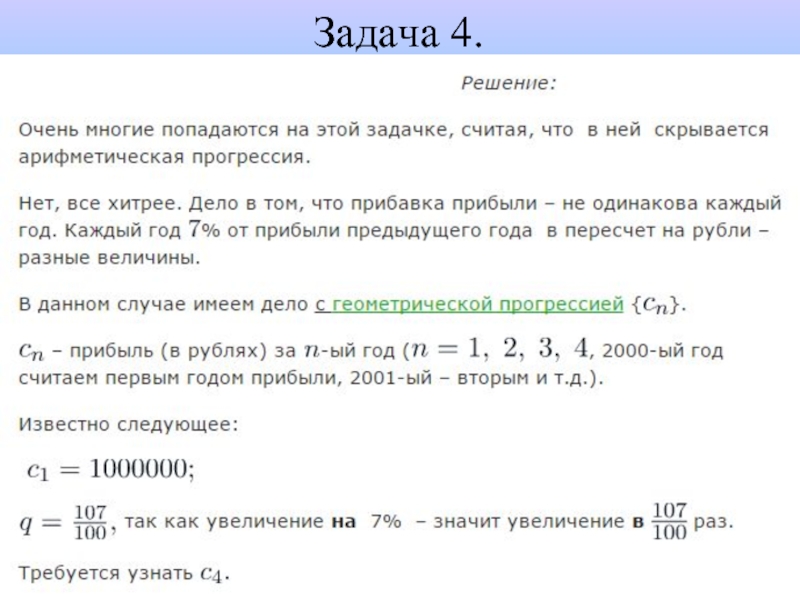
- 6. Задание 1. Задача 4.
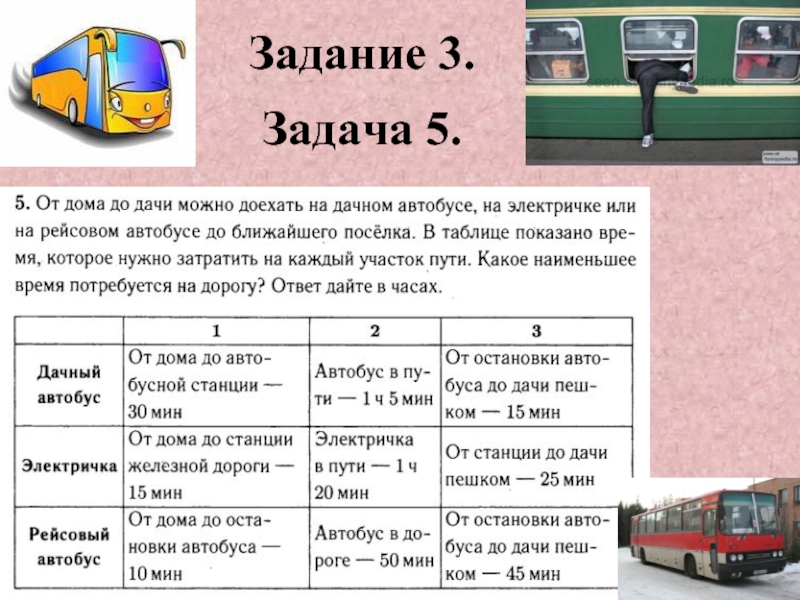
- 7. Задание 1. Задача 5.
- 8. Задание 1. Выпускники Ангарского медицинского колледжа
- 9. Задание 1. Задача 7.
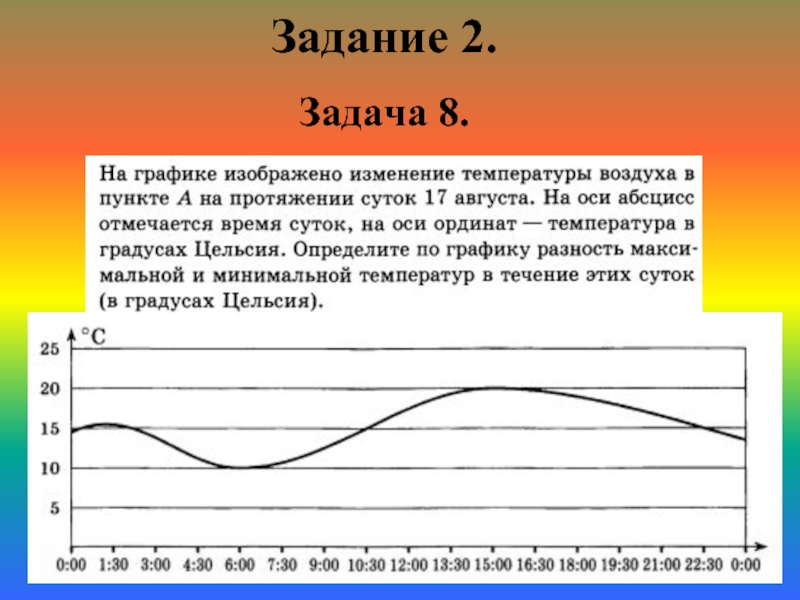
- 10. Задание 1. Задача 8.
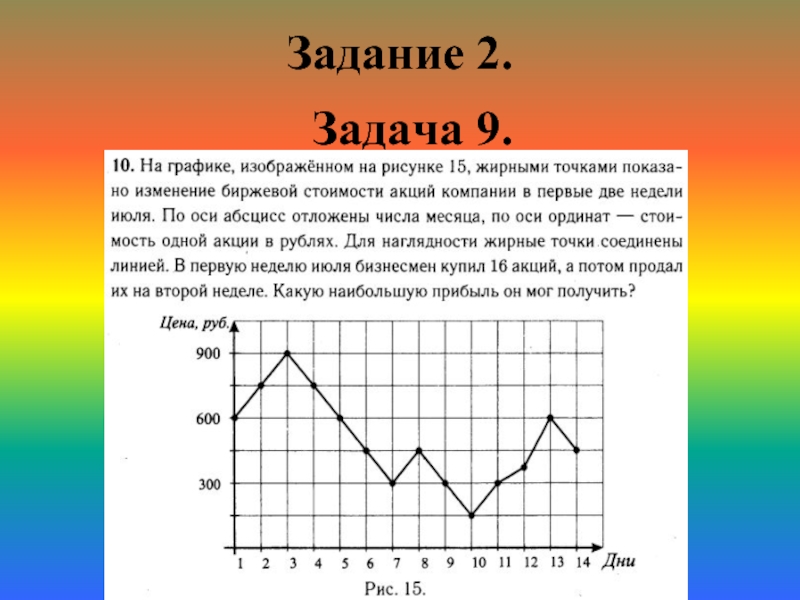
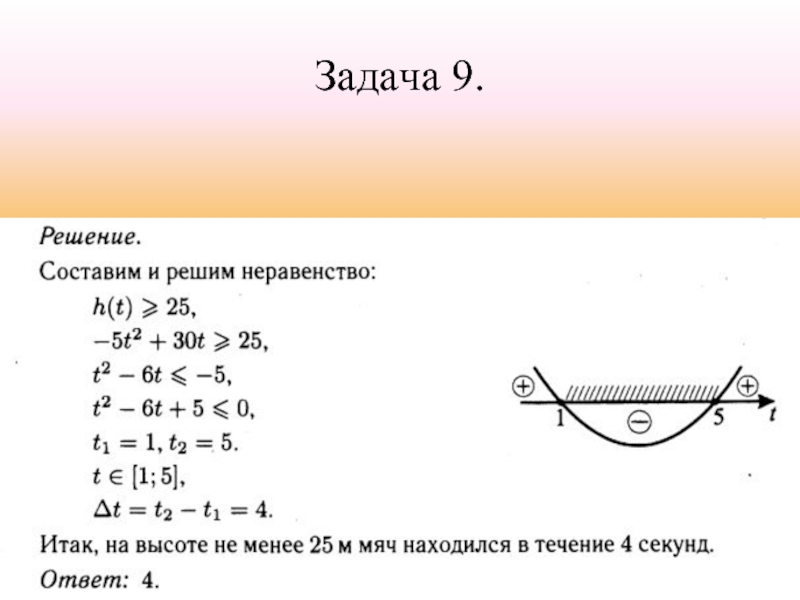
- 11. Задание 1. Задача 9.
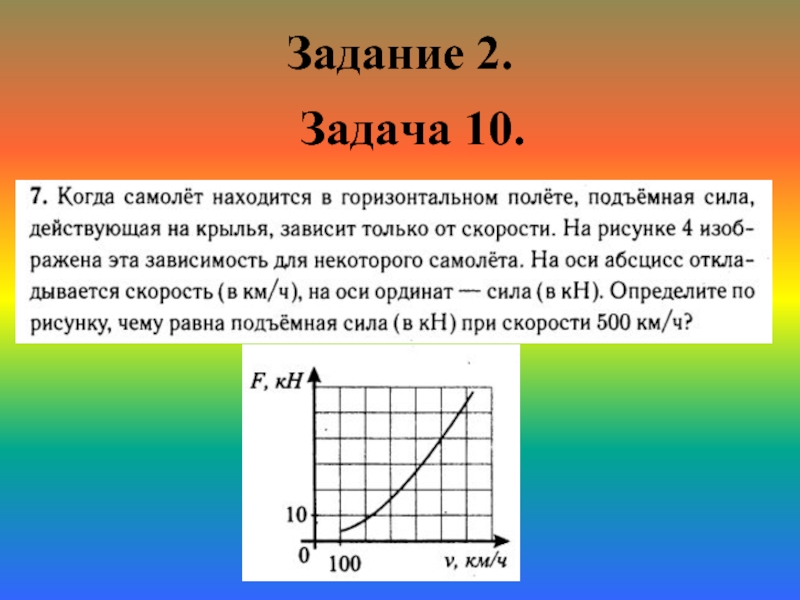
- 12. Задание 1. Задача 10.
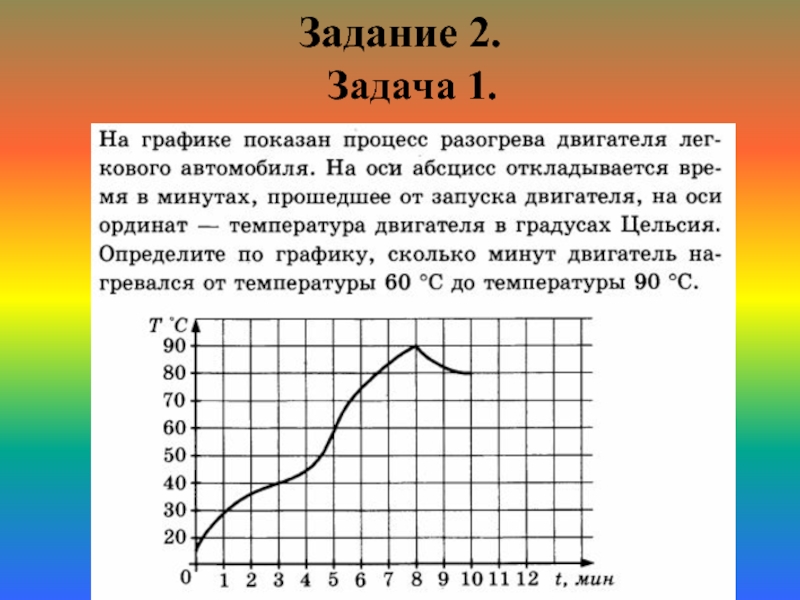
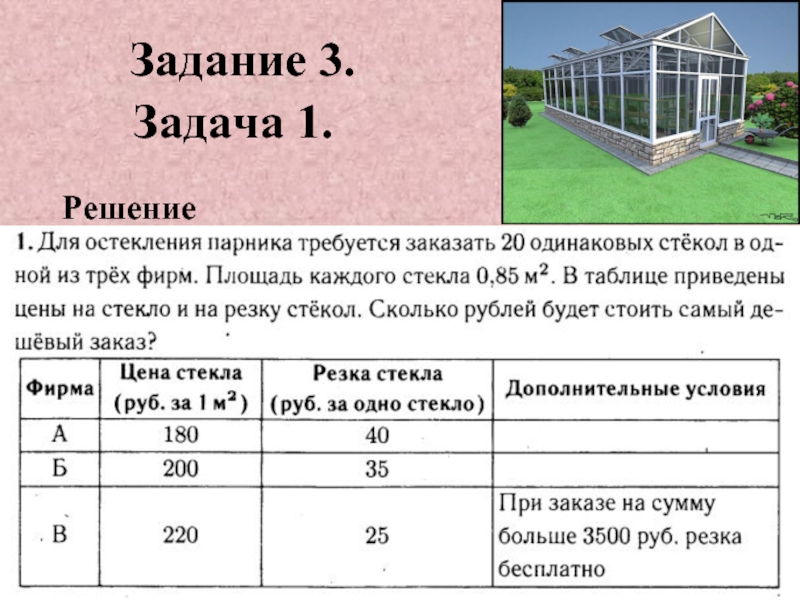
- 13. Задание 2. Задача 1.
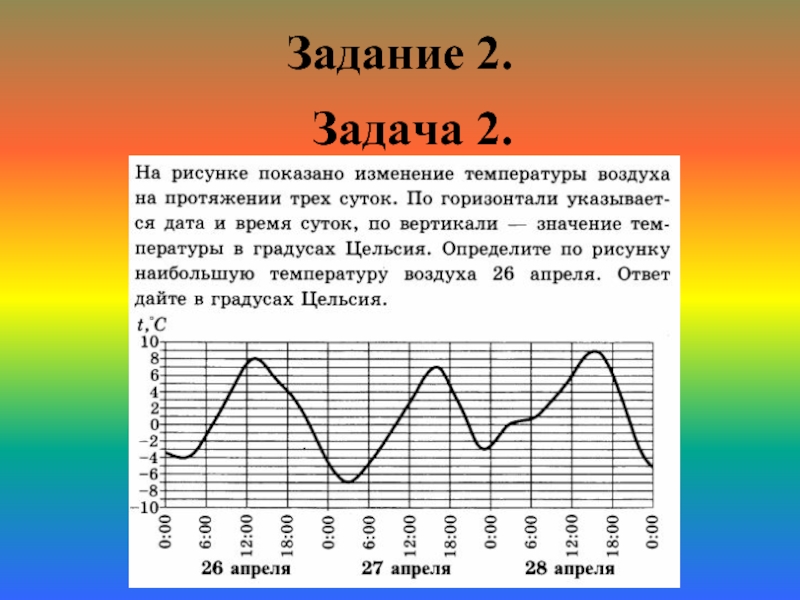
- 14. Задание 2. Задача 2.
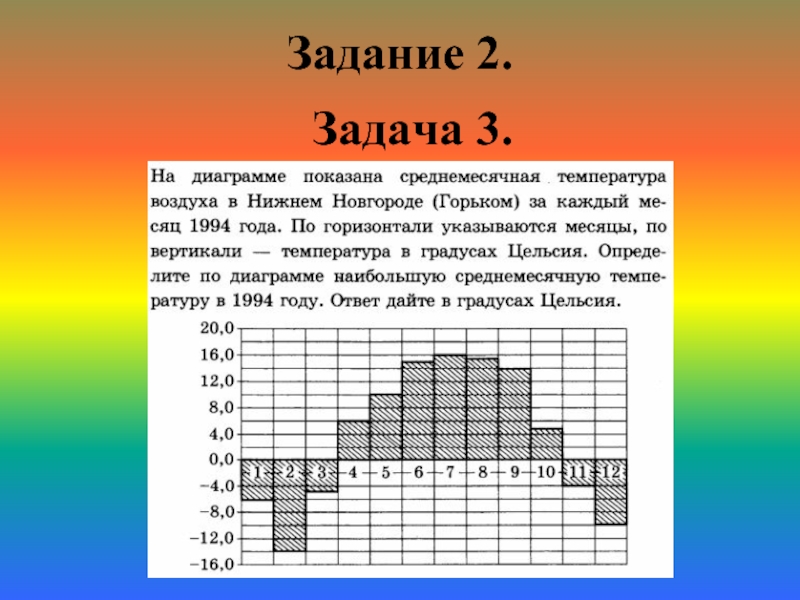
- 15. Задание 2. Задача 3.
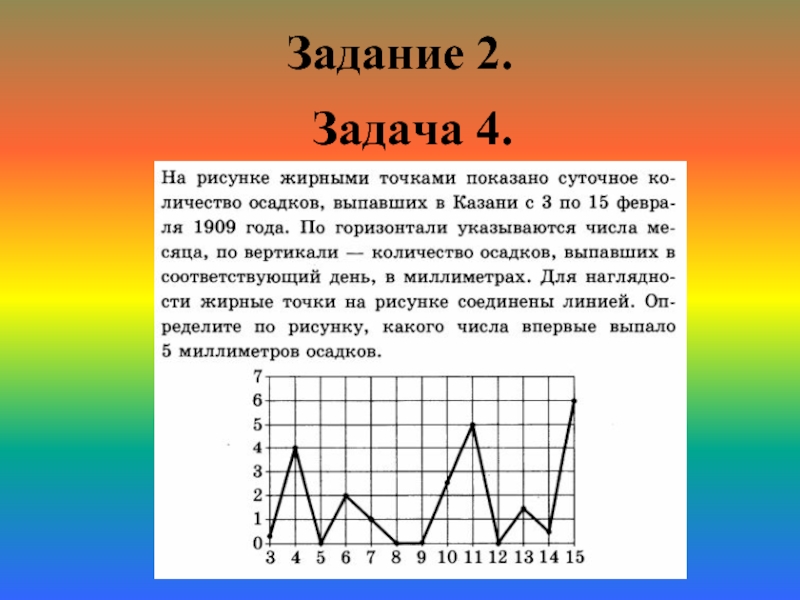
- 16. Задание 2. Задача 4.
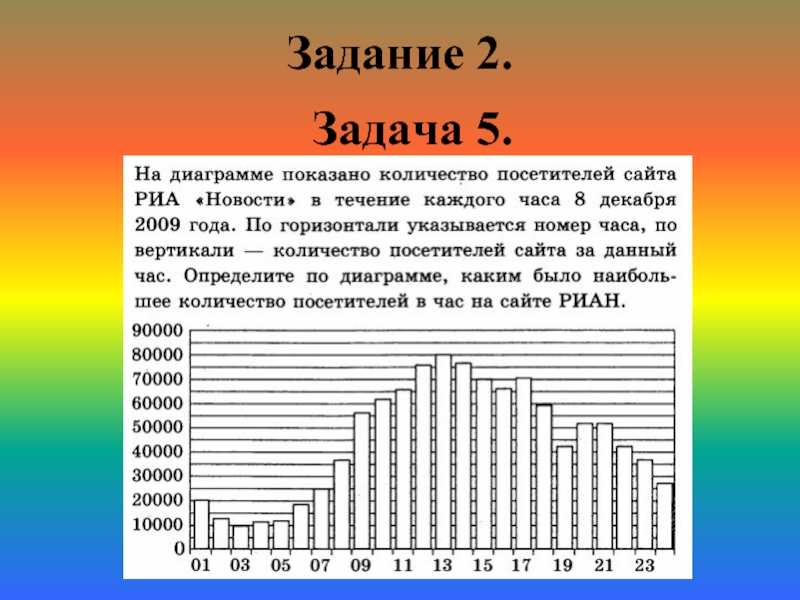
- 17. Задание 2. Задача 5.
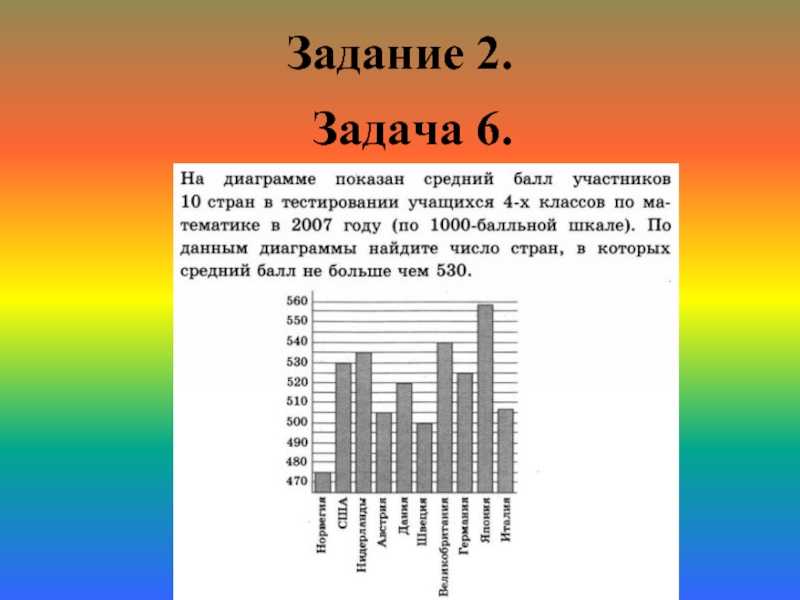
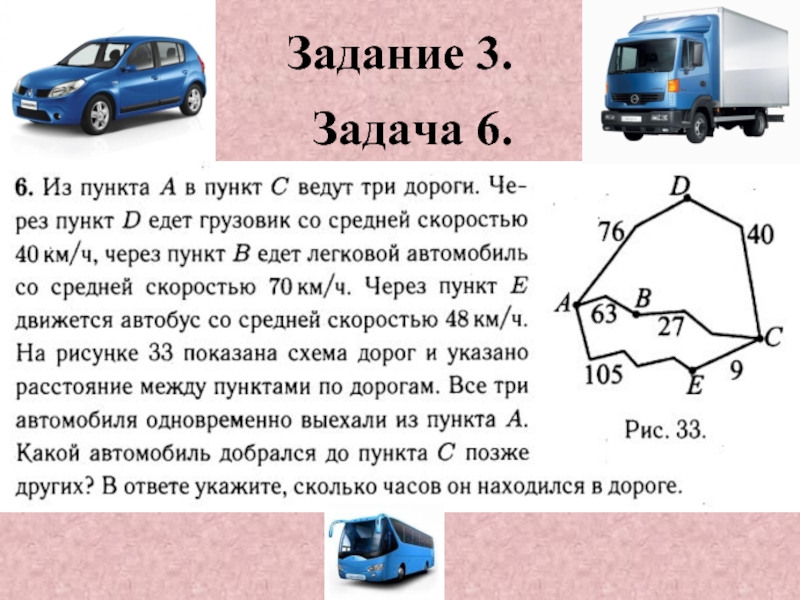
- 18. Задание 2. Задача 6.
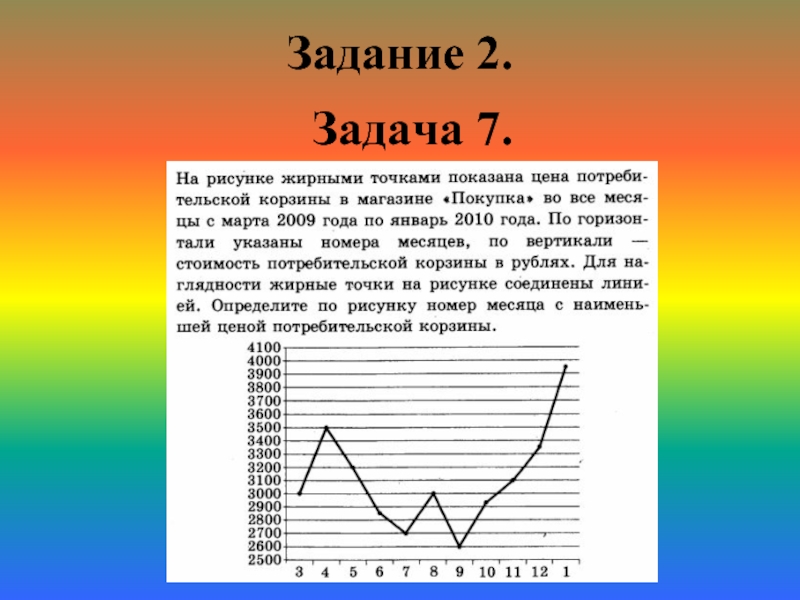
- 19. Задание 2. Задача 7.
- 20. Задание 2. Задача 8.
- 21. Задание 2. Задача 9.
- 22. Задание 2. Задача 10.
- 23. Задание 3. Задача 1. Решение
- 24. Задача 1.
- 25. Задание 3. Задача 2.
- 26. Задача 2.
- 27. Задание 3. Задача 3.
- 28. Задача 3.
- 29. Задание 3. Задача 4.
- 30. Задача 4.
- 31. Задание 3. Задача 5.
- 32. Задача 5.
- 33. Задание 3. Задача 6.
- 34. Задача 6.
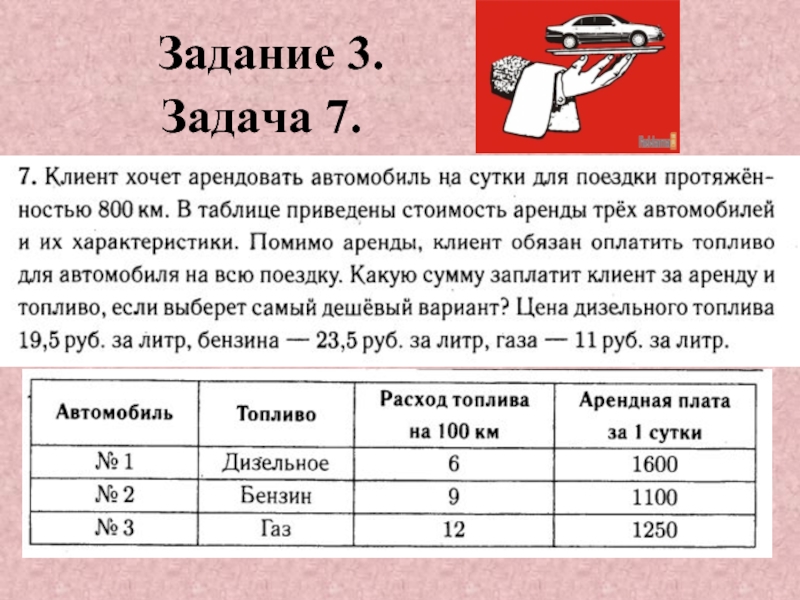
- 35. Задание 3. Задача 7.
- 36. Задача 7.
- 37. Задание 3. Задача 8.
- 38. Задача 8.
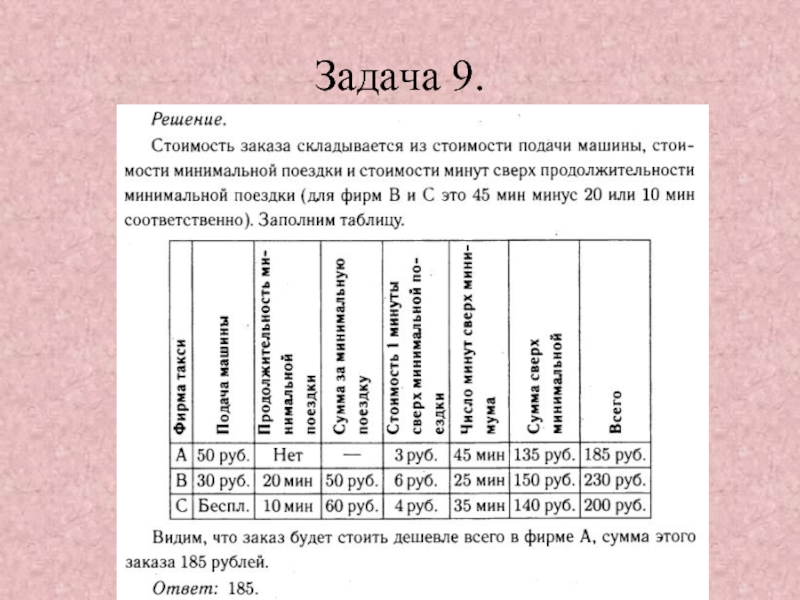
- 39. Задание 3. Задача 9.
- 40. Задача 9.
- 41. Задание 3. Задача 10.
- 42. Задача 10.
- 43. Задание 4. Задача 1.
- 44. Задача 1.
- 45. Задание 4. Задача 2.
- 46. Задача 2.
- 47. Задание 4. Задача 3.
- 48. Задача 3.
- 49. Задание 4. Задача 4.
- 50. Задача 4.
- 51. Задание 4. Задача 5.
- 52. Задача 5.
- 53. Задание 4. Задача 6.
- 54. Задача 6.
- 55. Задание 4. Задача 7.
- 56. Задача 7.
- 57. Задание 4. Задача 8.
- 58. Задача 8.
- 59. Задание 4. Задача 9.
- 60. Задача 9.
- 61. Задание 4. Задача 10.
- 62. Задача 10.
- 63. Задание 5. Задачи на среднюю скорость
- 64. Задание 5. Задачи на движение по воде. Задача 1.
- 65. Задача 3.
- 66. Задача 3.
- 67. Задание 5. Задача 2.
- 68. Задача 2.
- 69. Задача 2.
- 70. Задание 5. Задачи, решаемые с помощью прогрессий Задача 3.
- 71. Задача 3.
- 72. Задача 4
- 73. Задача 4.
- 74. Задача 4.
- 75. Решение: Ответ: 27. Семья состоит из
- 76. Решение: Ответ: 589 Виноград содержит 90%
- 77. Решение: Смешали некоторое количество 20-процентного раствора некоторого
Содержание:
Задание1. Несложная арифметическая текстовая задача, моделирующая реальную или близкую к реальной ситуацию
Задание 2. Задание на чтение графика функции (диаграммы), моделирующее реальную или близкую к реальной ситуацию.
Слайд 1Тема: «Применение математических методов для решения содержательных задач из различных областей
науки и практики»
Слайд 2
Содержание:
Задание1. Несложная арифметическая текстовая задача, моделирующая реальную или близкую к реальной
ситуацию
Задание 2. Задание на чтение графика функции (диаграммы), моделирующее реальную или близкую к реальной ситуацию.
Задание 3. Несложная текстовая задача на оптимальное решение.
Задание 4. Текстовое задание на анализ практической ситуации (экономические, физические, химические и др. процессы).
Задание 5. Традиционная текстовая задача, сводящаяся к составлению и решения уравнения.
Задание 5. Традиционная текстовая задача, сводящаяся к составлению и решения уравнения.
Слайд 3Задание 1.
Для ремонта квартиры требуется 45 рулонов обоев. Сколько пачек
обойного клея нужно купить, если одна пачка клея рассчитана на 8 рулонов?
Задача 1.
Ответ:
нужно купить 6 пачек обойного клея.
Решение:
45/8 = 5,625 т.е. 6 пачек клея.
Слайд 4Задание 1.
Задача 2.
Ответ:
38*25 = 950 (руб.)
950 – 890 =
60 (руб.)
Она потратила бы на 60 рублей меньше, если бы подписалась на журнал.
Решение:
Слайд 8Задание 1.
Выпускники Ангарского медицинского колледжа покупают цветы для последнего звонка:
букеты из 3 роз каждому преподавателю и из 7 роз классному руководителю и директору. Они собираются подарить цветы 15 преподавателям (включая директора и классного руководителя). Розы покупаются по оптовой цене 55 рублей за штуку. Сколько рублей стоят все розы?
Задача 6.
Слайд 75Решение:
Ответ: 27.
Семья состоит из мужа, жены и их дочери студентки.
Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Получим:
⇔
Т.е. зарплата жены составляет 27% общего дохода.
Задача 5.
Задание 5.
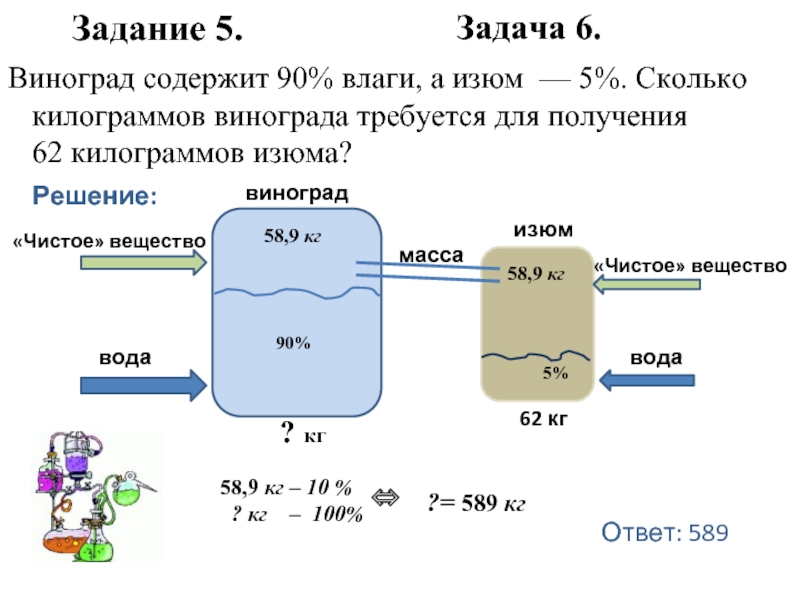
Слайд 76Решение:
Ответ: 589
Виноград содержит 90% влаги, а изюм — 5%. Сколько
килограммов винограда требуется для получения 62 килограммов изюма?
58,9 кг
58,9 кг
Задание 5.
Задача 6.
Слайд 77Решение:
Смешали некоторое количество 20-процентного раствора некоторого вещества с таким же количеством
16-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Ответ: 18
0,2x+0,16x = 0,36x = 0,18·2х
Задание 5.
Задача 6.
