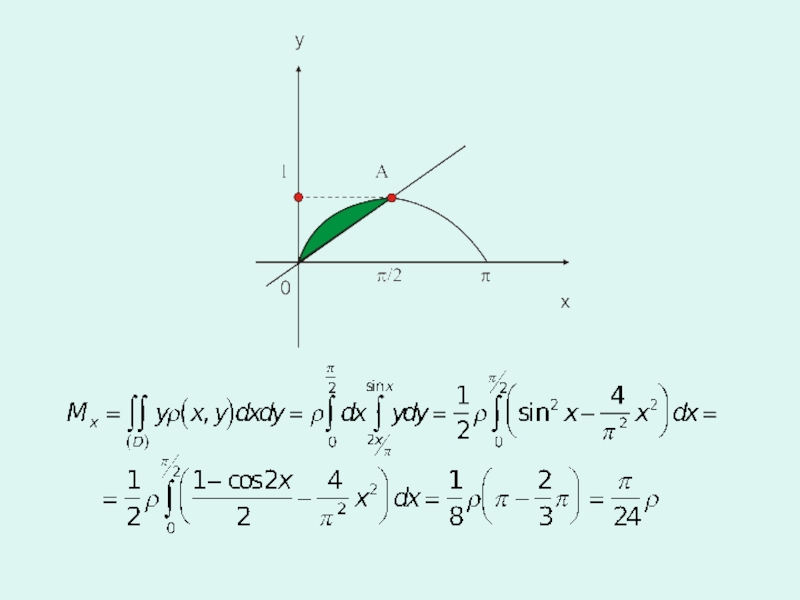- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение интеграла по фигуре от скалярной функции в механике презентация
Содержание
- 1. Применение интеграла по фигуре от скалярной функции в механике
- 2. Вычисление массы материальной фигуры. - стержень,
- 3. - поверхность (Q), тогда
- 4. Пример Найти массу пластинки, имеющей
- 6. Решаем задачу с применением формулы
- 7. Вычисление статических моментов. Определение 1 Статическим
- 8. Определение 2 Статическими моментами
- 9. Определение 3 Статическими моментами
- 10. Пример Найти статический момент относительно оси
- 12. Координаты центра масс материальной фигуры Для
- 13. Пример Найти центр масс однородного цилиндрического тела, ограниченного поверхностями
- 15. Вследствие симметрии
- 16. Моменты инерции Определение Моментом инерции материальной
- 17. момент инерции плоской пластины (D)
- 18. Моменты инерции тела относительно координатных плоскостей
- 19. Пример Найти момент инерции кругового
- 21. Вычисления проведем в цилиндрических координатах,
Вычисление массы материальной фигуры. - стержень, совпадающий с отрезком интегрирования, тогда -дуга линии (L), тогда - плоская область (D), тогда (*)
Слайд 2Вычисление массы материальной фигуры.
- стержень, совпадающий с отрезком интегрирования, тогда
-дуга линии (L), тогда
- плоская область (D), тогда
(*)
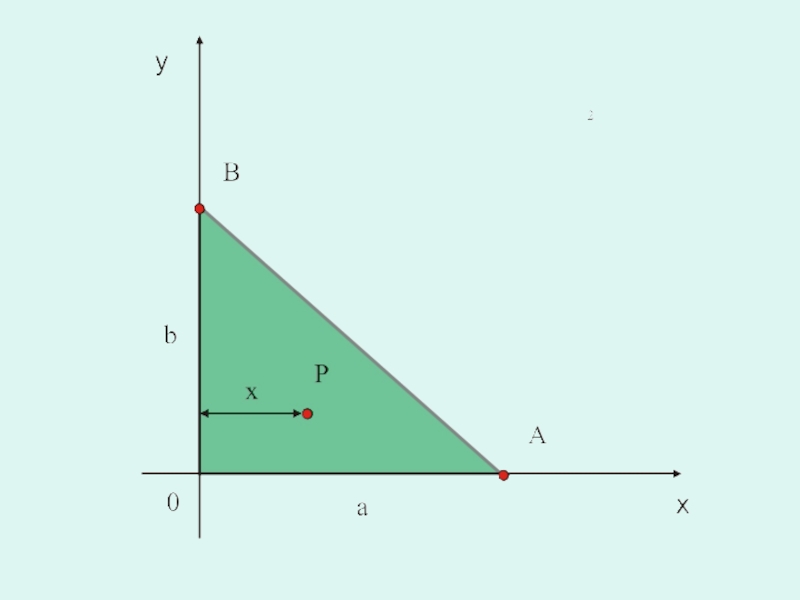
Слайд 4Пример
Найти массу пластинки, имеющей форму прямоугольного треугольника с
катетами ОА=а,
ОВ=b, если плотность в любой точке Р равна расстоянию от точки Р до катета ОВ.
Слайд 7Вычисление статических моментов.
Определение 1 Статическим моментом материальной точки относительно прямой
(точки, плоскости)
называется произведение ее массы на расстояние от точки до прямой (точки, плоскости).
называется произведение ее массы на расстояние от точки до прямой (точки, плоскости).
Слайд 8
Определение 2 Статическими моментами плоской системы n
материальных точек
относительно осей декартовой прямоугольной системы координат называются выражения:
где - сосредоточенные в точках массы; - абсциссы и ординаты соответствующих точек.
где - сосредоточенные в точках массы; - абсциссы и ординаты соответствующих точек.
Слайд 9Определение 3
Статическими моментами и плоской
фигуры относительно осей
декартовой прямоугольной системы координат называются выражения:
при условии, что указанные пределы существуют и не зависят от способа построения интегральной суммы
декартовой прямоугольной системы координат называются выражения:
при условии, что указанные пределы существуют и не зависят от способа построения интегральной суммы
Слайд 10Пример
Найти статический момент относительно оси Ох однородной фигуры, ограниченной синусоидой
и
прямой ОА, проходящей через начало координат и точку синусоиды .
Для определения воспользуемся формулой
уравнение прямой ОА имеет вид
прямой ОА, проходящей через начало координат и точку синусоиды .
Для определения воспользуемся формулой
уравнение прямой ОА имеет вид
Слайд 15
Вследствие симметрии
Вычислим тройные интегралы в цилиндрической системе координат.
Для области
(V) имеем
Слайд 16Моменты инерции
Определение Моментом инерции материальной точки массой m относительно начала
координат
(относительно оси Ох - , относительно плоскости Оху - ) называется произведение массы
точки на квадрат расстояния до начала координат( соответственно оси Ох, плоскости Оху)
(относительно оси Ох - , относительно плоскости Оху - ) называется произведение массы
точки на квадрат расстояния до начала координат( соответственно оси Ох, плоскости Оху)
Слайд 17
момент инерции плоской пластины (D) относительно координатных осей прямоугольной декартовой
системы координат вычисляются по формулам
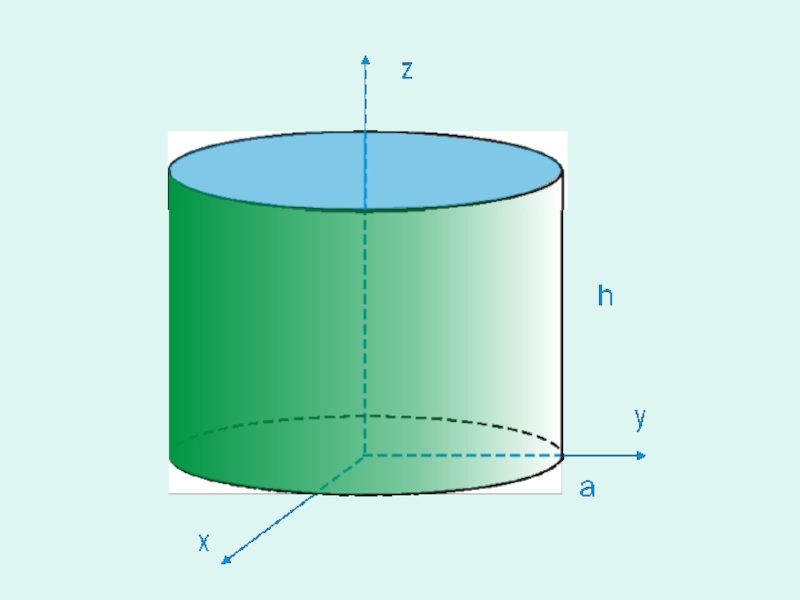
Слайд 19Пример
Найти момент инерции кругового цилиндра ,
высота которого h и
радиуса a относительно оси,
служащей диаметром основания цилиндра .
служащей диаметром основания цилиндра .
Слайд 21
Вычисления проведем в цилиндрических координатах, при этом уравнение цилиндра примет
вид r = a
Пределы интегрирования
Имеем:
Пределы интегрирования
Имеем:
