бывает трудно найти первообразную функции.
Поэтому используются численные методы, позволяющие найти приближенное значение определенного интеграла с заданной точностью.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение формулы Ньютона-Лейбница презентация
Содержание
- 1. Применение формулы Ньютона-Лейбница
- 2. Основной принцип построения формул приближенного вычисления
- 3. Пусть на отрезке [a,b] задана непрерывная
- 4. Для этого разобьем [a,b] на n
- 5. S S S
- 6. где каждое слагаемое представляет собой площадь трапеции:
- 7. Тогда Все слагаемые, кроме первого и последнего повторяются дважды.
- 8. Учитывая, что получаем формула трапеций
- 9. Обозначим выражение в правой части как
- 10. Доказано, что
- 11. Пример. Вычислить при n=5. Оценить погрешность.
- 12. Решение. n=5, следовательно длина отрезков разбиения
- 13. Найдем погрешность: Эта функция монотонно убывает
- 14. 2. Формула Симпсона В основе формулы
- 15. Разобьем [a,b] на 2n равных частей.
- 17. формула Симпсона
- 18. Пусть М4 - максимальное значение модуля
- 19. Пример. Вычислить при n=2.
- 20. Решение. n=2, следовательно полное число узлов равно 5. Тогда
Основной принцип построения формул приближенного вычисления определенного интеграла состоит в замене частичных криволинейных трапеций, образующихся при разбиении отрезка интегрирования, на более простые фигуры.
Слайд 1
12.9. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ
ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Применение формулы Ньютона-Лейбница бывает сложным, так как
Слайд 2
Основной принцип построения формул
приближенного вычисления определенного
интеграла состоит в замене частичных
криволинейных трапеций, образующихся при
разбиении отрезка интегрирования, на более
простые фигуры.
Слайд 3
Пусть на отрезке [a,b] задана непрерывная неотрицательная функция y=f(x).
Тогда интеграл
равен
площади под кривой y=f(x) на отрезке [a,b].
Мы получим приближенное значение этого интеграла, если вместо площади под кривой возьмем площадь под ломаной, подходящей достаточно близко к этой кривой.
Мы получим приближенное значение этого интеграла, если вместо площади под кривой возьмем площадь под ломаной, подходящей достаточно близко к этой кривой.
1. Формула трапеций
Слайд 4
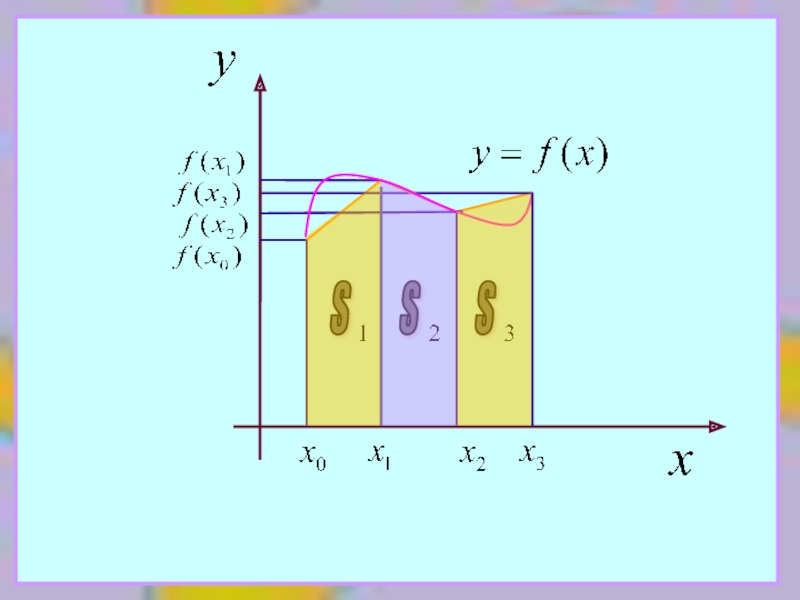
Для этого разобьем [a,b] на n равных частей длиной
и на каждом
из отрезков разбиения
где
заменим участок кривой y=f(x) хордой, стягивающей концевые точки.
Слайд 9
Обозначим выражение в правой части как S(n). Тогда абсолютная погрешность от
применения формулы трапеций составит
Пусть М2 - максимальное значение модуля второй производной подынтегральной функции на [a,b]:
Слайд 13
Найдем погрешность:
Эта функция монотонно убывает на данном отрезке, следовательно она достигает
своего максимального значения в крайней левой точке при х=1.
Слайд 14
2. Формула Симпсона
В основе формулы Симпсона лежит замена двух соседних частичных
криволинейных трапеций, ограниченных сверху функцией y=f(x) на криволинейную трапецию, ограниченную сверху параболой вида
Поэтому формулу Симпсона часто называют формулой парабол.
Слайд 15
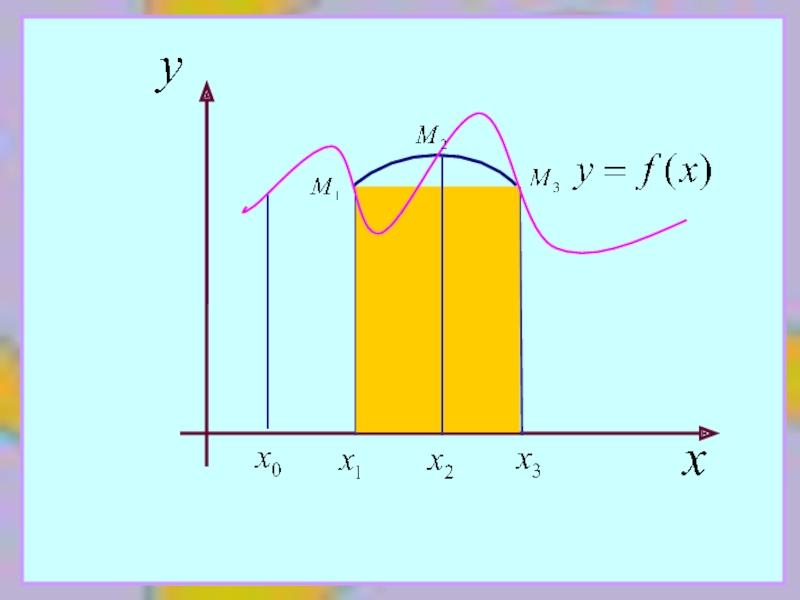
Разобьем [a,b] на 2n равных частей. Тогда кривая разобьется прямыми
на 2n
частей точками М0, М1,...М2n.
Через каждую тройку точек М0, М1, М2… проведем параболу. Коэффициенты А,В,С находятся из условия ее прохождения через тройку точек.
Через каждую тройку точек М0, М1, М2… проведем параболу. Коэффициенты А,В,С находятся из условия ее прохождения через тройку точек.
Таким образом, криволинейная трапеция, ограниченная сверху функцией y=f(x), заменяется составной фигурой, ограниченной сверху n параболами.
Слайд 18
Пусть М4 - максимальное значение модуля четвертой производной подынтегральной функции на
[a,b]:
Тогда погрешность вычислений по формуле Симпсона оценивается как:
