- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация1 презентация
Содержание
- 1. Презентация1
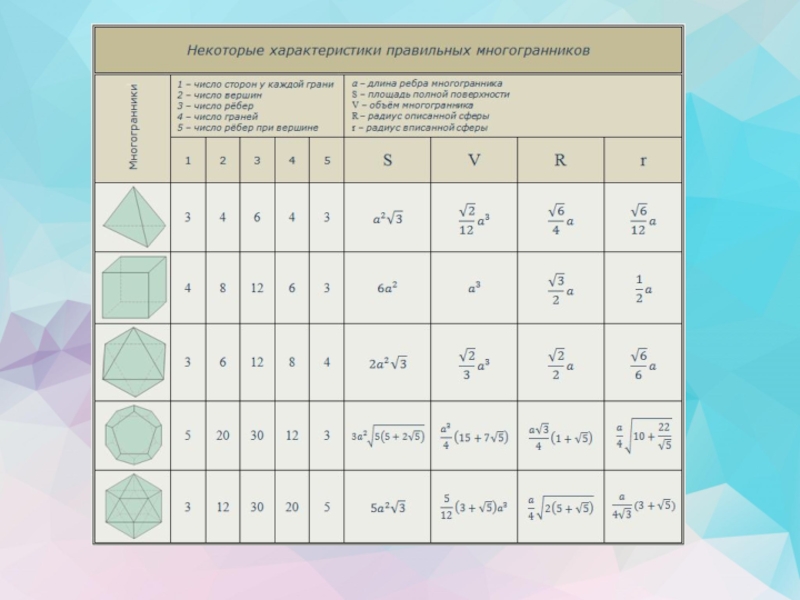
- 2. Многогранник – это поверхность, составленная из многоугольников
- 3. Многогранники могут быть выпуклые и невыпуклые. Многогранник
- 5. Призмой называется многогранник, состоящий из двух плоских
- 7. Сечения призмы плоскостями, параллельными боковым рёбрам,являются параллелограммами.
- 8. Пирамидой (например, SABCDE) называется многогранник, который состоит из
- 9. Сечения пирамиды плоскостями, проходящими через ее вершину, представляют
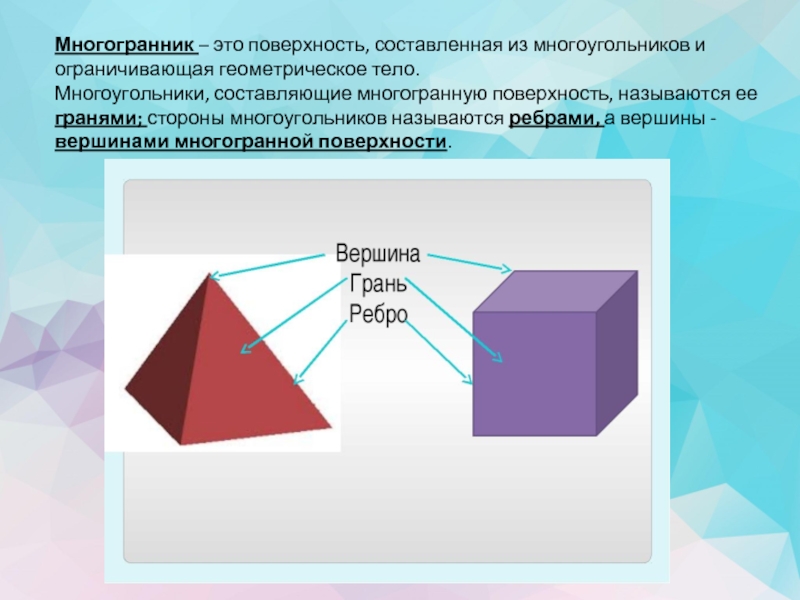
Слайд 2Многогранник – это поверхность, составленная из многоугольников и ограничивающая геометрическое тело.
Многоугольники,
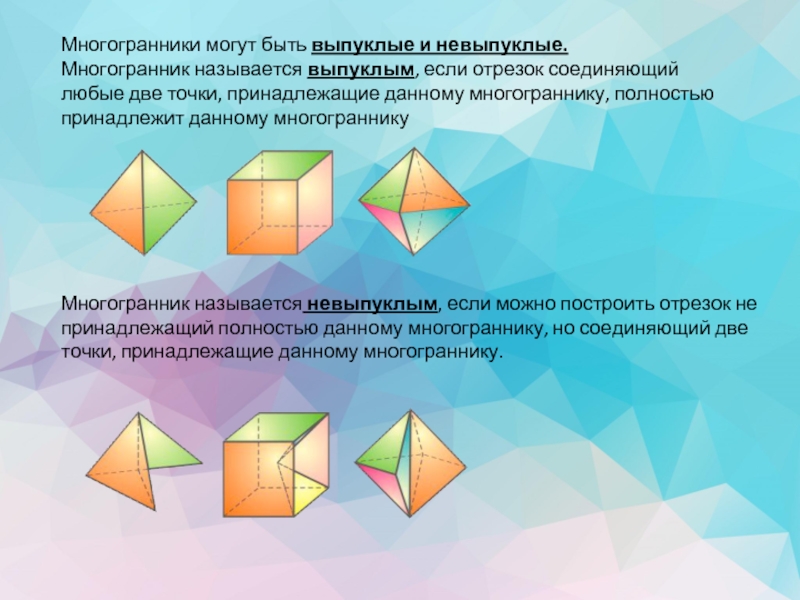
Слайд 3Многогранники могут быть выпуклые и невыпуклые.
Многогранник называется выпуклым, если отрезок соединяющий любые
Многогранник называется невыпуклым, если можно построить отрезок не принадлежащий полностью данному многограннику, но соединяющий две точки, принадлежащие данному многограннику.
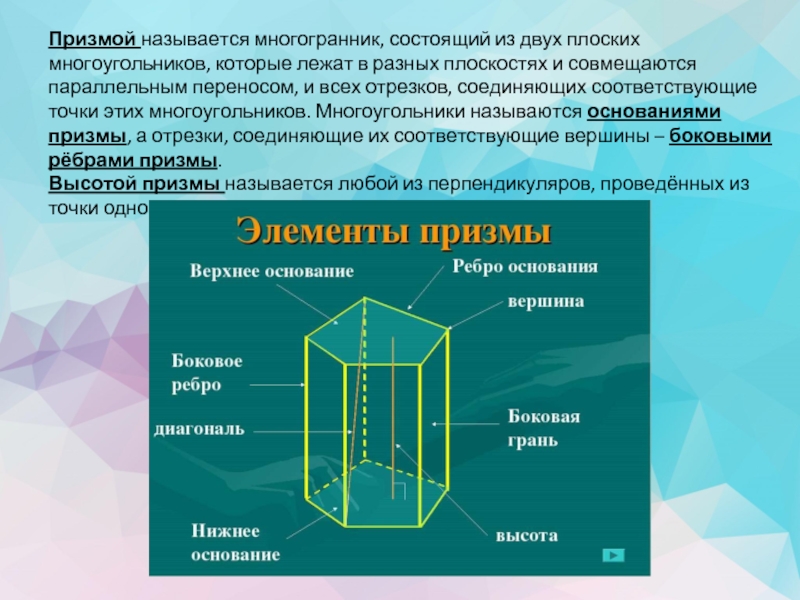
Слайд 5Призмой называется многогранник, состоящий из двух плоских многоугольников, которые лежат в
Высотой призмы называется любой из перпендикуляров, проведённых из точки одного основания к плоскости другого основания призмы.
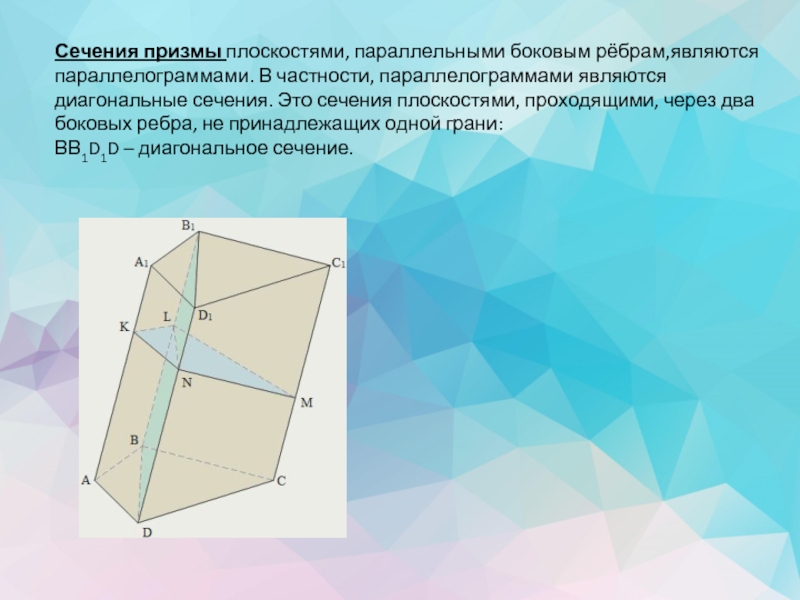
Слайд 7Сечения призмы плоскостями, параллельными боковым рёбрам,являются параллелограммами. В частности, параллелограммами являются
ВВ1D1D – диагональное сечение.
Слайд 8Пирамидой (например, SABCDE) называется многогранник, который состоит из плоского многоугольника (пятиугольник ABCDE) –
Отрезки (SA, SB, SC, SD, SE), соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Поверхность пирамиды состоит из основания (пятиугольник ABCDE) и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей стороной – сторона основания пирамиды:
ΔSAB, ΔSBC, ΔSCD, ΔSDE, ΔSEA – боковые грани.
Боковой поверхностью пирамиды называется сумма площадей ее боковых граней.
Высотой пирамиды (SО) называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания.
Объём пирамиды равен трети произведения площади основания на высоту пирамиды:
V = 1/3·Sоснh.
Площадь полной поверхности любой пирамиды равна сумме площадей боковой поверхности и основания:
Sп = Sб + Sосн.