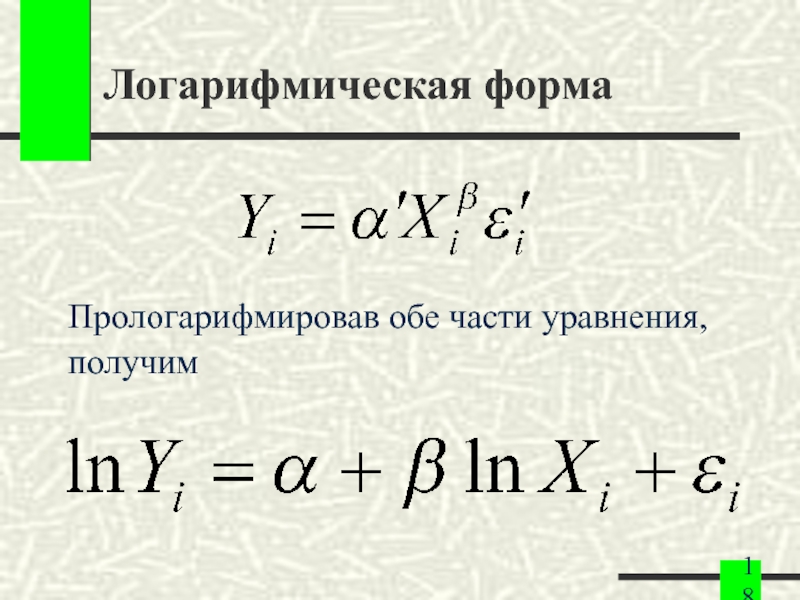- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Преобразование переменных в парной регрессии презентация
Содержание
- 1. Преобразование переменных в парной регрессии
- 2. Цели лекции Понять смысл нелинейной регрессии Научиться выполнять преобразования переменных Экономическая интерпретация регрессионной модели
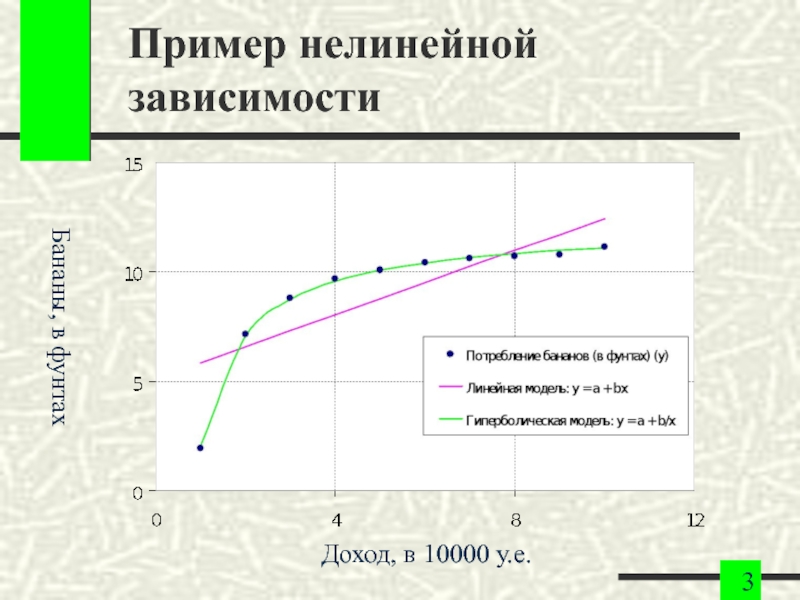
- 3. Пример нелинейной зависимости Бананы, в фунтах Доход, в 10000 у.е.
- 4. Направления анализа и развития парной линейной регрессии
- 5. Этапы построения модели 1. Выбор теоретических предпосылок
- 6. Производственная функция Кобба-Дугласа Многие экономические процессы не
- 7. Анализ экономического роста Анализ теоретических предпосылок: прирост
- 8. Классы нелинейных регрессий Различают два класса нелинейных
- 9. Альтернативные функциональные формы: правила выбора Правила выбора
- 10. Линейная форма Интерпретация коэффициента регрессии β − предельный эффект независимого фактора
- 11. Линейная форма Для полученных оценок a, b уравнения регрессии:
- 12. Линейная форма Коэффициент регрессии b показывает прирост
- 13. Линейная форма от времени
- 14. Моделирование эластичности Независимо от вида математической связи
- 15. Пример расчета эластичности Рассмотрим кривую Энгеля:
- 16. Эластичность – переменная величина Например, для линейной
- 17. Средний коэффициент эластичности Средний коэффициент эластичности показывает,
- 18. Логарифмическая форма Прологарифмировав обе части уравнения, получим
- 19. Логарифмическая форма Интерпретация коэффициента регрессии β –
- 20. Логарифмическая форма Вычисление наклона (скорости роста)
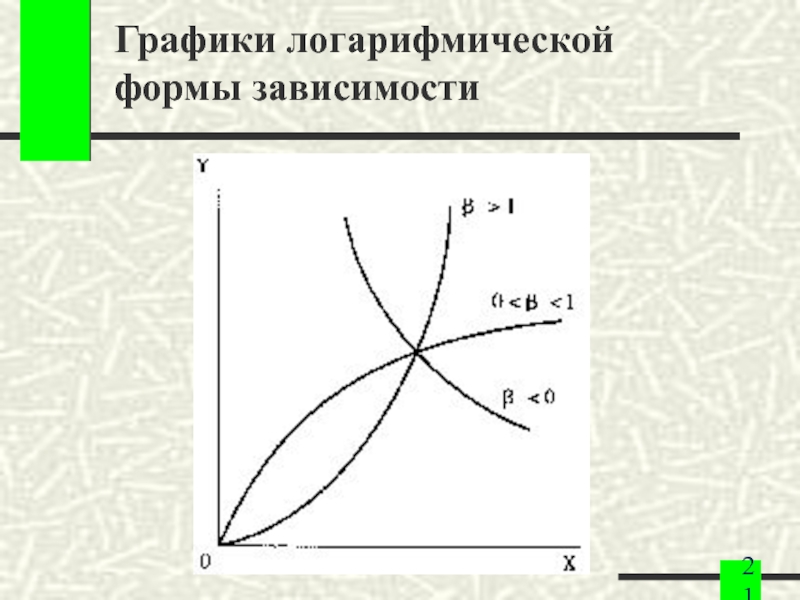
- 21. Графики логарифмической формы зависимости
- 22. Полулогарифмические формы 1. Линейно-логарифмическая форма (логарифм
- 23. Линейно-логарифмическая форма Интерпретация коэффициента регрессии β:
- 24. Линейно-логарифмическая форма Эластичность убывает с ростом Y:
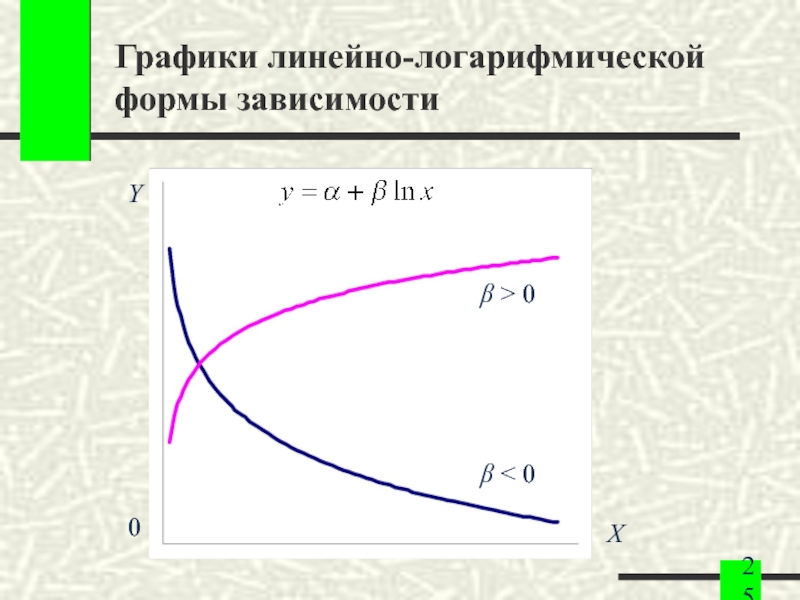
- 25. Графики линейно-логарифмической формы зависимости 0 X Y β > 0 β < 0
- 26. Логарифмически-линейная форма Интерпретация коэффициента регрессии β:
- 27. Логарифмически-линейная форма Эластичность растет с ростом Y:
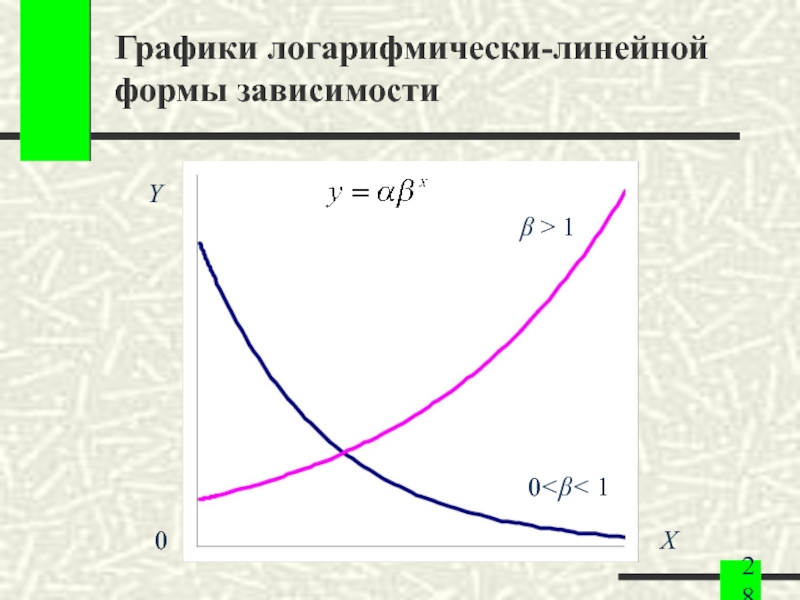
- 28. Графики логарифмически-линейной формы зависимости Y β > 1 0
- 29. Логарифмически-линейная форма от времени Вид уравнения:
- 30. Обратные зависимости Вычисление эластичности С ростом
- 31. Сводка результатов для альтернативных функциональных форм в парной регрессии
- 32. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 33. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 34. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 35. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 36. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 37. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 38. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 39. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 40. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 41. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 42. Сводка линеаризующих преобразований для основных зависимостей в экономике
- 43. Преобразование случайного отклонения Пример. Логарифмирование
- 44. Признаки качественной модели 1. Простота модели (из
- 45. Сравнение различных моделей 1. Содержательный анализ 2. Формальный анализ: Метод Зарембки Преобразование Бокса-Кокса
- 46. Метод Зарембки Применим для выбора из двух
- 47. Сравнение различных моделей парной регрессии методом Зарембки
- 48. Сравнение различных моделей парной регрессии методом Зарембки
- 49. Метод Бокса-Кокса Идея метода. Переменная
- 50. Сравнение различных моделей парной регрессии методом Бокса-Кокса
- 51. Сравнение различных моделей парной регрессии методом Бокса-Кокса
- 52. Конец лекции
Слайд 2Цели лекции
Понять смысл нелинейной регрессии
Научиться выполнять преобразования переменных
Экономическая интерпретация регрессионной модели
Слайд 4Направления анализа и развития парной линейной регрессии
Ключевые точки (начало координат)
Кривая или
прямая
Форма криволинейной зависимости
Вспомогательные экономические показатели (скорость и темп роста, эластичность)
Уточнение формы (экстремумы, пределы)
Сравнение функциональных форм
Форма криволинейной зависимости
Вспомогательные экономические показатели (скорость и темп роста, эластичность)
Уточнение формы (экстремумы, пределы)
Сравнение функциональных форм
Слайд 5Этапы построения модели
1. Выбор теоретических предпосылок
2. Формализация предпосылок
3. Построение математической модели
4.
Анализ построенной модели
Слайд 6Производственная функция Кобба-Дугласа
Многие экономические процессы не являются
линейными по сути. Их моделирование
линейными
уравнениями не даст положительного результата.
уравнениями не даст положительного результата.
Пример. Производственная функция Кобба – Дугласа
Y – объем выпуска; K, L – затраты капитала и труда; α, β – параметры модели.
Слайд 7Анализ экономического роста
Анализ теоретических предпосылок: прирост
пропорционален накопленному потенциалу
Формализация предпосылок:
Интерпретация и анализ:
коэффициент регрессии β − годовой темп роста, возможно сопоставление с реальными данными
Слайд 8Классы нелинейных регрессий
Различают два класса нелинейных регрессий:
1. Регрессии, нелинейные относительно переменных,
но линейные по оцениваемым параметрам.
2. Регрессии, нелинейные по оцениваемых параметрам.
2. Регрессии, нелинейные по оцениваемых параметрам.
Регрессии, нелинейные относительно объясняющих переменных, всегда сводятся к линейным моделям.
Слайд 9Альтернативные функциональные формы: правила выбора
Правила выбора формы зависимости:
1. Исходить из экономической
теории.
2. Оценивать формальное качество модели.
3. Дополнительно проверять по нескольким содержательным критериям.
4. Ответить на вопросы, возникающие при анализе модели:
каковы признаки качественной модели;
какие ошибки спецификации встречаются и каковы их последствия;
как обнаружить ошибку спецификации;
каким образом можно исправить ошибку спецификации и перейти к более качественной модели.
2. Оценивать формальное качество модели.
3. Дополнительно проверять по нескольким содержательным критериям.
4. Ответить на вопросы, возникающие при анализе модели:
каковы признаки качественной модели;
какие ошибки спецификации встречаются и каковы их последствия;
как обнаружить ошибку спецификации;
каким образом можно исправить ошибку спецификации и перейти к более качественной модели.
Слайд 10Линейная форма
Интерпретация коэффициента регрессии
β − предельный эффект независимого фактора
Слайд 12Линейная форма
Коэффициент регрессии b показывает прирост
зависимой переменной при изменении
объясняющей переменной
на единицу.
Коэффициент регрессии b – угловой коэффициент линии регрессии
Коэффициент регрессии a – среднее значение зависимой переменной при нулевом значении объясняющей переменной
Слайд 13Линейная форма от времени
Интерпретация коэффициента регрессии от времени − ежегодный (ежемесячный
и т.д.) прирост зависимой переменной
Слайд 14Моделирование эластичности
Независимо от вида математической связи
между Y и X эластичность равна:
Эластичность
y по x рассчитывается как относительное изменение y на единицу относительного изменения x.
Слайд 15Пример расчета эластичности
Рассмотрим кривую Энгеля:
где Y – спрос на товар, X
– доход. Имеем:
Эластичность =
Эластичность =
Например для модели эластичность спроса по доходу равна 0,3. Иными словами, изменение дохода (X) на 1% вызывает изменение спроса (Y) на 0,3%
Слайд 16Эластичность – переменная величина
Например, для линейной модели
Эластичность не всегда бывает постоянной
для различных значений X и Y
Слайд 17Средний коэффициент эластичности
Средний коэффициент эластичности
показывает, на сколько процентов в среднем по
совокупности
изменится результат Y от своей
средней величины при изменении фактора X на
1% от своего среднего значения
средней величины при изменении фактора X на
1% от своего среднего значения
Слайд 19Логарифмическая форма
Интерпретация коэффициента регрессии β – эластичность
зависимой переменной по объясняющей переменной
Коэффициент при объясняющей переменной показывает,
на сколько процентов возрастает Y при возрастании X на 1%.
Логарифмическую форму следует использовать там, где есть основание предполагать постоянство эластичности
Слайд 20Логарифмическая форма
Вычисление наклона (скорости роста)
Наклон постоянно меняется с изменением номера
наблюдения
Слайд 22Полулогарифмические формы
1. Линейно-логарифмическая форма
(логарифм при объясняющей переменной)
2. Логарифмически-линейная форма
(логарифм при
зависимой переменной)
Слайд 23Линейно-логарифмическая форма
Интерпретация коэффициента регрессии β:
Коэффициент при объясняющей переменной показывает
на сколько единиц
возрастает Y при возрастании X на 1%
При интерпретации коэффициент следует делить на 100
Если X увеличится на 1%, то прирост Y составит β /100 единиц (в которых измеряется Y)
Слайд 24Линейно-логарифмическая форма
Эластичность убывает с ростом Y:
Это указывает на класс зависимостей, где
следует применять линейно-логарифмическую форму регрессии
Логарифм при X снижает влияние роста X (степень влияния X снижается с ростом X). Моделирование эффектов насыщения на уровне скорости роста: «возрастание с убывающей скоростью»
Слайд 26Логарифмически-линейная форма
Интерпретация коэффициента регрессии β:
Коэффициент при объясняющей переменной показывает
на сколько процентов
возрастает Y при возрастании X на
одну единицу
одну единицу
При интерпретации коэффициент следует умножать на 100
Слайд 27Логарифмически-линейная форма
Эластичность растет с ростом Y:
Это указывает на класс зависимостей, где
следует применять линейно-логарифмическую форму регрессии
Моделирование эффектов насыщения на уровне скорости роста: «возрастание с возрастающей скоростью»
Примеры: кривые Энгеля для товаров роскоши, моделирование оплаты труда (процентная надбавка за стаж и опыт)
Слайд 29Логарифмически-линейная форма от времени
Вид уравнения:
Интерпретация:
Коэффициент при переменной времени выражает темп
прироста. Он
показывает на сколько процентов (если
умножить его на 100) возрастает Y ежегодно
умножить его на 100) возрастает Y ежегодно
Эту функциональную форму удобно использовать для моделирования процессов экономического роста
Слайд 30Обратные зависимости
Вычисление эластичности
С ростом X зависимая переменная приближается к некоторому
числу (моделирование эффекта насыщения)
Пример: Моделирование потребления товаров первой необходимости (быстрое достижение насыщения)
Слайд 43Преобразование случайного отклонения
Пример.
Логарифмирование нелинейной модели с аддитивным
случайным членом не приводит к
линеаризации
соотношения относительно параметров.
соотношения относительно параметров.
МНК применяется к преобразованным (линеаризованным) уравнениям. Поэтому необходимо особое внимание уделять рассмотрению свойств случайных отклонений – выполнимости предпосылок теоремы Гаусса-Маркова.
Слайд 44Признаки качественной модели
1. Простота модели (из примерно одинаково отражающих реальность моделей,
выбирается та, которая содержит меньше объясняющих переменных.
2. Единственность (для любых данных коэффициенты модели должны вычисляться однозначно).
3. Максимальное соответствие (модель тем лучше, чем больше скорректированный коэффициент детерминации).
4. Согласованность с теорией (уравнение регрессии должно соответствовать теоретическим предпосылкам).
5. Прогнозные качества (прогнозы, полученные на основе модели, должны подтверждаться реальностью).
2. Единственность (для любых данных коэффициенты модели должны вычисляться однозначно).
3. Максимальное соответствие (модель тем лучше, чем больше скорректированный коэффициент детерминации).
4. Согласованность с теорией (уравнение регрессии должно соответствовать теоретическим предпосылкам).
5. Прогнозные качества (прогнозы, полученные на основе модели, должны подтверждаться реальностью).
Слайд 45Сравнение различных моделей
1. Содержательный анализ
2. Формальный анализ:
Метод Зарембки
Преобразование Бокса-Кокса
Слайд 46Метод Зарембки
Применим для выбора из двух форм
(несравнимых непосредственно), в одной
из которых
зависимая переменная входит с
логарифмом, а в другой – нет
логарифмом, а в другой – нет
Метод позволяет сравнить линейную и логарифмическую регрессии и оценить значимость наблюдаемых различий
Слайд 47Сравнение различных моделей парной регрессии методом Зарембки
1. Вычисляем среднее геометрическое значений
зависимой переменной и все ее значения делим на это среднее:
2. Рассчитываются линейная и логарифмическая
регрессии, и сравниваются значения их сумм квадратов
остатков (RSS)
2. Рассчитываются линейная и логарифмическая
регрессии, и сравниваются значения их сумм квадратов
остатков (RSS)
Слайд 48Сравнение различных моделей парной регрессии методом Зарембки
3. Вычисляем χ2-статистику для оценки
значимости
различий
4. Сравниваем с критическим значением
χ2-распределения . Различия значимы на уровне значимости α, если
различий
4. Сравниваем с критическим значением
χ2-распределения . Различия значимы на уровне значимости α, если
Слайд 49Метод Бокса-Кокса
Идея метода. Переменная
:
при λ=1 превращается в линейную функцию
при λ→0 переходит в логарифм
при λ=1 превращается в линейную функцию
при λ→0 переходит в логарифм
Плавно изменяя λ, можно постепенно перейти от линейной регрессии к логарифмической, все время сравнивая качество
Слайд 50Сравнение различных моделей парной регрессии методом Бокса-Кокса
1. Преобразуют зависимую переменную по
методу Зарембки:
2. Рассчитывают новые переменные (преобразование Бокса-Кокса) при значениях λ от 1 до 0:
2. Рассчитывают новые переменные (преобразование Бокса-Кокса) при значениях λ от 1 до 0:
Слайд 51Сравнение различных моделей парной регрессии методом Бокса-Кокса
3. Рассчитывают уравнения регрессии для
новых переменных при значениях λ от 1 до 0:
4. Определяют минимальное значение суммы квадратов остатков (SSR).
5. Выбирают одну из крайних регрессий, к которой ближе точка минимума.
4. Определяют минимальное значение суммы квадратов остатков (SSR).
5. Выбирают одну из крайних регрессий, к которой ближе точка минимума.
