- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предел и непрерывность функции презентация
Содержание
- 1. Предел и непрерывность функции
- 2. Бесконечно малая и бесконечно большие величины.
- 3. Переменная величина у называется бесконечно большой, если
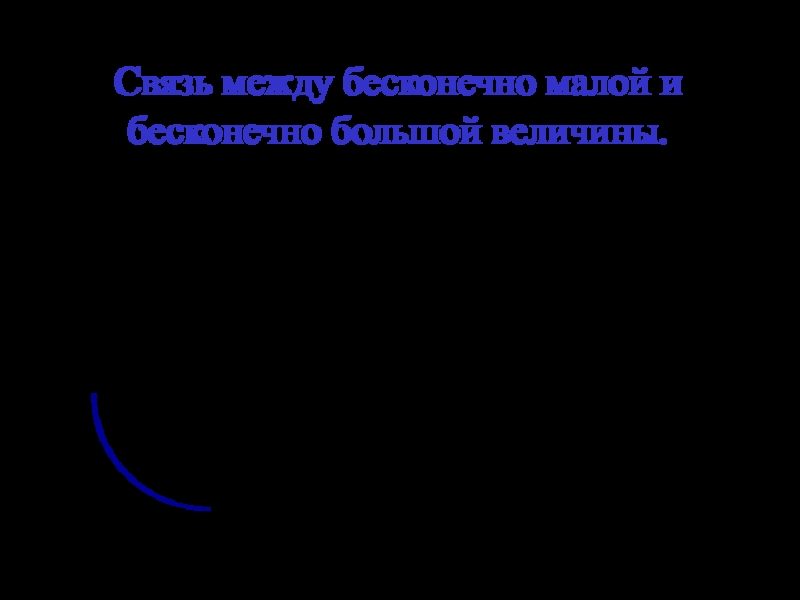
- 4. Связь между бесконечно малой и бесконечно большой
- 5. пример: 1) , тогда
- 6. Предел переменной Число
- 7. Постоянная а называется пределом переменной х,
- 8. Предел функции
- 9. Определение «на языке последовательности» Число а
- 10. Односторонние пределы. Пределы функций при х→х0-
- 11. Определение «на языке последовательности»: если f(x)
- 12. Пример.
- 13. Связь между односторонними пределами. Теорема.
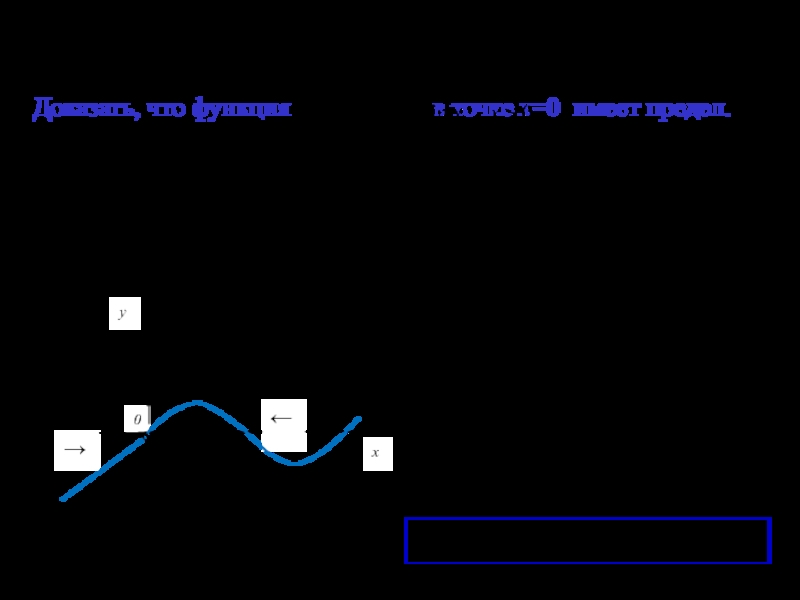
- 14. Доказать, что функция в точке
- 15. Доказать, что функция в точке
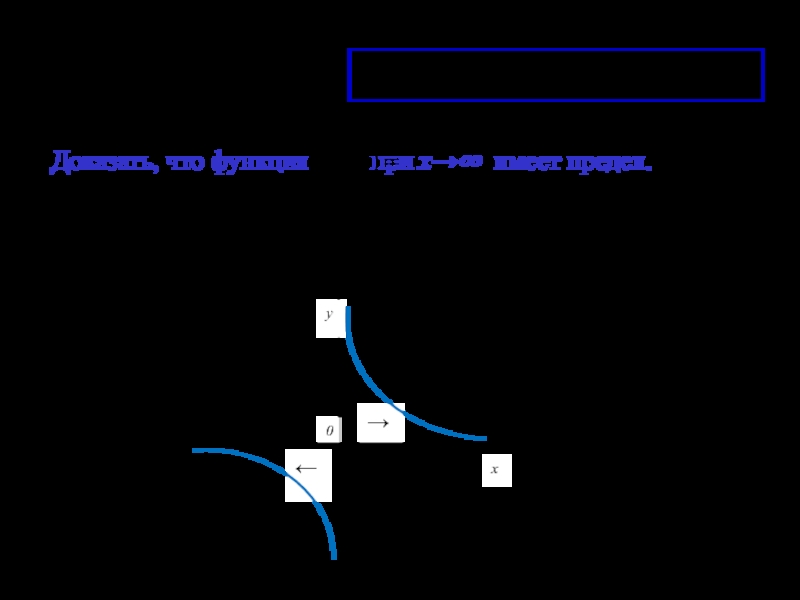
- 16. Пределы функций при х→∞, х→ - ∞
- 17. Определение «на языке последовательности»: число а
- 18. Справедлива теорема Доказать, что
- 19. Бесконечно малые и бесконечно большие функции.
- 20. Пример: 1) функция есть
- 21. Функция f(x) называется бесконечно большой функцией (или
- 22. Замечание. Функция y=f(x) при х→х0 или при
- 23. Основные теоремы о пределах
- 24. Основные теоремы о пределах
- 25. I.Вычисление пределов функций. 1) Вычислить
- 26. 2) Вычислить
- 27. II. Вычисление пределов функций. Предел знаменателя равен
- 28. 4) Вычислить
- 29. 5) Вычислить
- 30. III. Вычисление пределов функций. Предел
- 31. 7) Вычислить
Слайд 2Бесконечно малая и бесконечно большие величины.
Переменная величина α называется бесконечно
-1
1
0
или
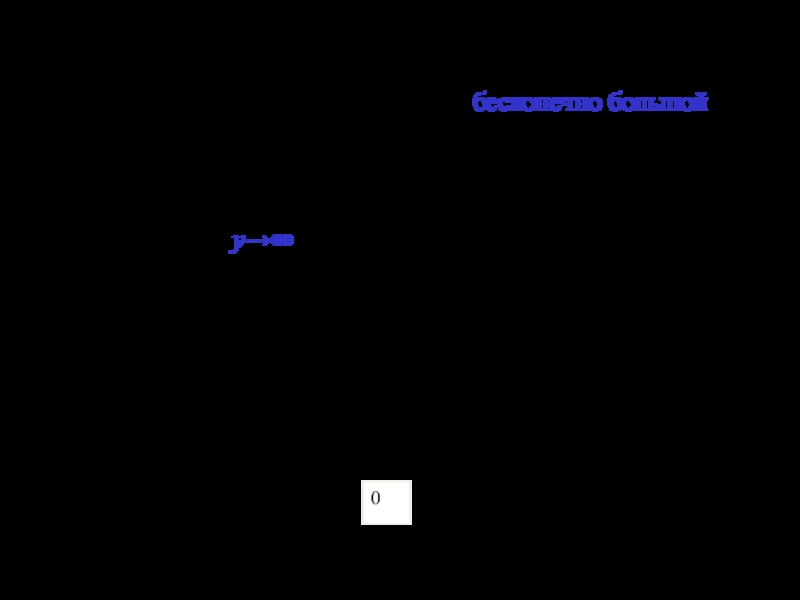
Слайд 3Переменная величина у называется бесконечно большой, если она изменяется так, что
у→∞
или
0
Слайд 7 Постоянная а называется пределом переменной х, если разность между ними
, если
или
Слайд 9Определение «на языке последовательности»
Число а называется пределом функции f(x) в точке
при
или
Слайд 10Односторонние пределы.
Пределы функций при х→х0- и х→х0+
Определение «на языке последовательности»:
если
Слайд 11Определение «на языке последовательности»:
если f(x) стремится к пределу а при х→х0
Слайд 13Связь между односторонними пределами.
Теорема. Функция f(x) имеет в точке х0 предел
Слайд 16Пределы функций при х→∞, х→ - ∞ и х→+∞
Определение «на языке
число а называется пределом функции f(x) при х→∞, если для всех значений х бесконечно большой последовательности значения функции f(x) сколь угодно мало отличаются от а (f(x) →а) и пишут
Слайд 17Определение «на языке последовательности»:
число а называется пределом функции f(x) при х→+∞
и пишут
Слайд 19Бесконечно малые и бесконечно большие функции.
Функция α=α(х) называется бесконечно малой
Аналогично определяются бесконечно малые функции при х→х0- , х→х0+, х→-∞, х→+∞, х→∞.
Бесконечно малые функции обладают такими же свойствами, что и бесконечно малая переменная величина.
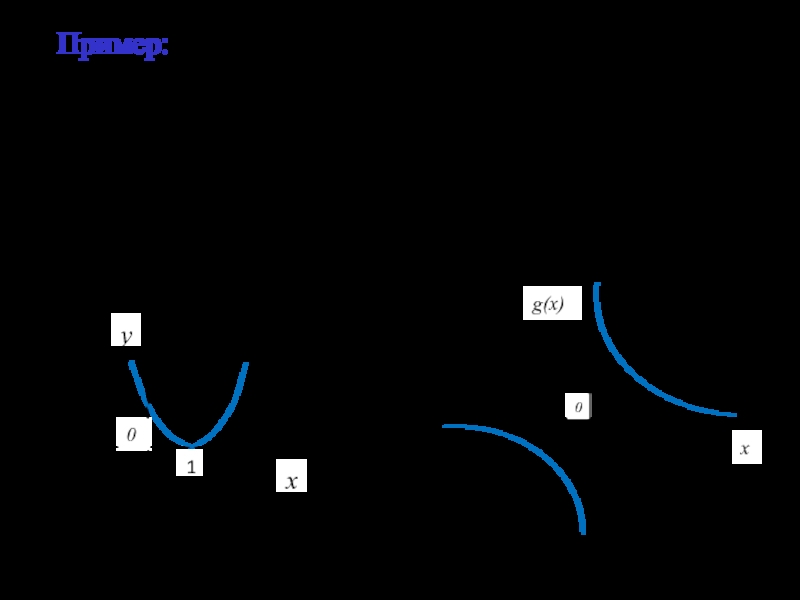
Слайд 20Пример:
1) функция есть бесконечно малая при х→1, т.к
2) функция
есть бесконечно малая при х→∞, т.к
g(x)
x
0
y
x
0
1
Слайд 21Функция f(x) называется бесконечно большой функцией (или просто бесконечно большой) в
Аналогично определяются бесконечно большие функции при х→х0- , х→х0+, х→-∞, х→+∞, х→∞.
Если f(x) стремится к бесконечности при х→х0 и при этом принимает только положительные или только отрицательные значения, соответственно пишут
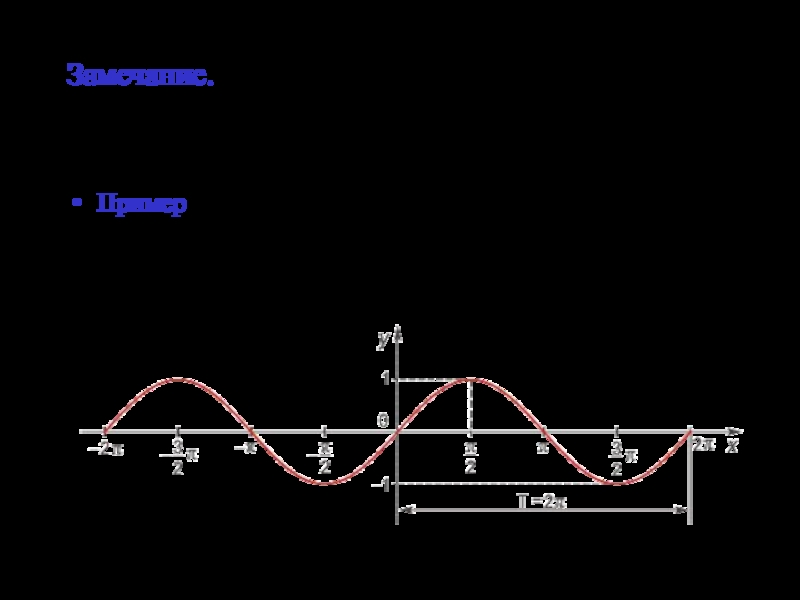
Слайд 22Замечание. Функция y=f(x) при х→х0 или при х→∞ может не стремиться
Пример. Функция y=sinx, определенная на всем числовом интервале, при х→∞ не стремится ни к конечному пределу, ни к бесконечности.
Слайд 24Основные теоремы о пределах
7) Пусть функции f(x), g(x) и h(x) определены
Пусть, кроме того, выполняется неравенство:
Тогда
Слайд 26
2) Вычислить
убедимся, что предел знаменателя отличен от 0:
тогда применима теорема
Слайд 27II. Вычисление пределов функций.
Предел знаменателя равен 0.
3) Вычислить
⇒ (3х-12)
малая величина, а обратная ей величина есть бесконечно большая.
Слайд 30
III. Вычисление пределов функций.
Предел функции при х→∞.
6) Вычислить
(4х+3) при х→∞ есть бесконечно большая величина,
а обратная ей величина есть бесконечно малая.
Слайд 32
Для раскрытия неопределенности вида
числитель и знаменатель дроби надо делить на