тесно связано понятие функции
в бесконечности.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предел функции в бесконечности презентация
Содержание
- 1. Предел функции в бесконечности
- 2. Этот предел функции обозначается
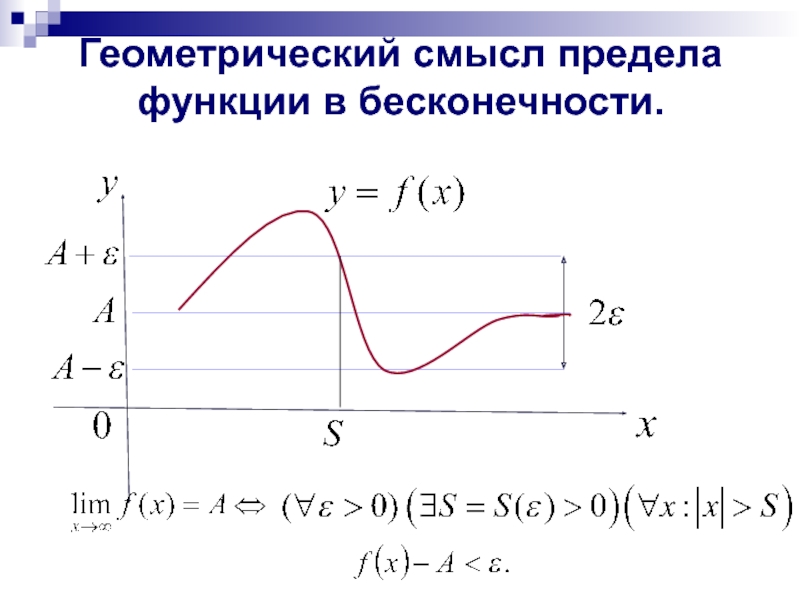
- 3. Геометрический смысл предела функции в бесконечности.
- 4. Замечание. Приведенное выше определение предела при
- 5. ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ Определение 2.
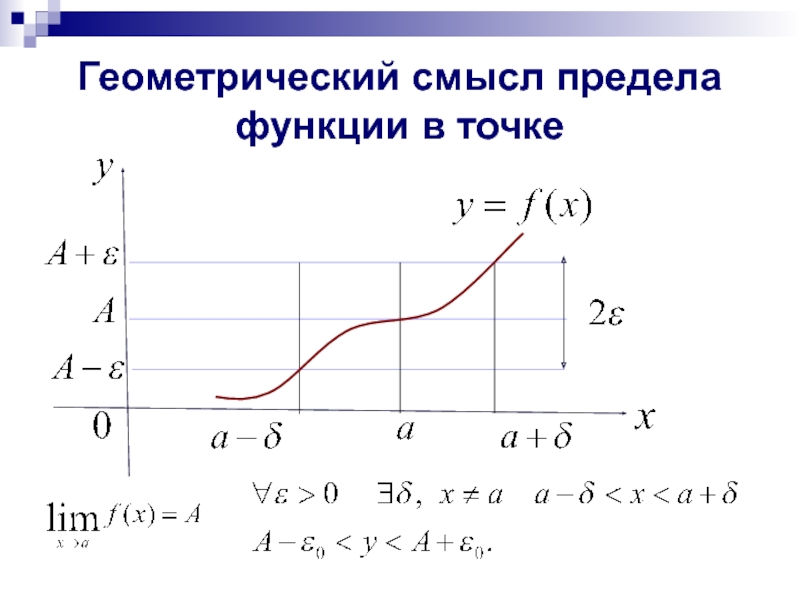
- 6. Геометрический смысл предела функции в точке
- 7. Замечание 1. Определение предела не требует существования
- 8. Односторонние пределы Определение 3. Число A называется
- 9. Определение 4. Говорят, что функция
- 10. Бесконечно малые величины их свойства
- 11. Теорема 2. Если функцию
- 12. Основные свойства бесконечно малых величин 1. Алгебраическая
- 13. ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛА 1) 2) Справедливо
- 14. 5) Если Если существуют конечные пределы:
- 15. 9) 10)
- 16. а) Если при замене
- 17. В таком случае задача вычисления предела
- 18. Примеры П р и м е р
- 19. П р и м е р
- 20. П р и м е р 5.
- 21. П р и м е р 7.
- 22. П р и м е р 8.
- 23. Непрерывность функции. О п р
- 24. Из свойств предела вытекает следующее утверждение. Т
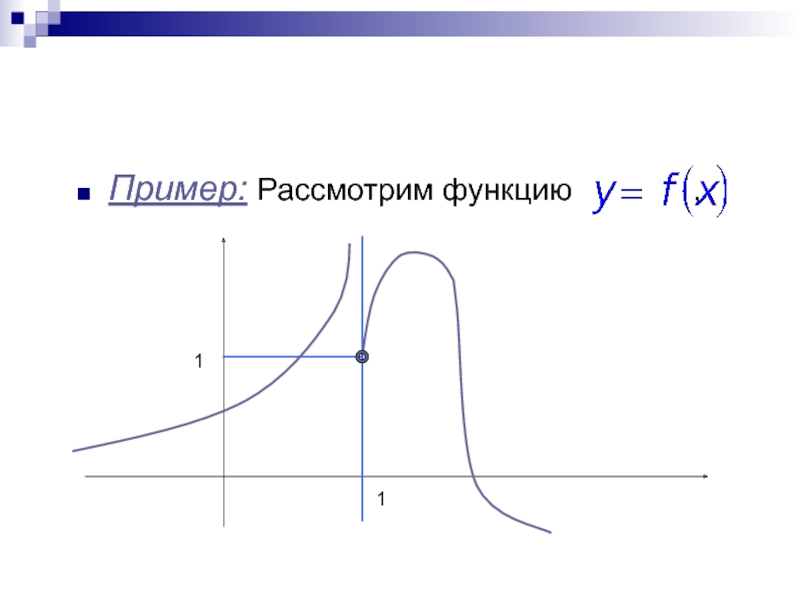
- 25. Пример: Рассмотрим функцию
- 26. О п р е д е л
- 27. Точки разрыва функции О п р
- 28. О п р е д е л
- 29. О п р е д е л
- 30. у х 1
- 31. Пример. Функция
- 32. Т е о р е м а
Этот предел функции обозначается или при С помощью логических
Слайд 4Замечание. Приведенное выше определение предела при
предполагает неограниченное возрастание независимой переменной по абсолютной величине. Можно сформулировать понятие предела при и В первом случае основное неравенство
выполняется для всех а во втором
случае для всех
выполняется для всех а во втором
случае для всех
Слайд 5ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
Определение 2. Число A называется пределом (по
Коши) функции в точке a (или при ), если для любого сколь угодно малого положительного числа найдется отвечающее ему положительное число такое, что для всех значений аргумента
, удовлетворяющих условию
справедливо неравенство:
Для обозначения предела используют символику:
, удовлетворяющих условию
справедливо неравенство:
Для обозначения предела используют символику:
(или
при
).
Слайд 7Замечание 1. Определение предела не требует существования функции в самой точке
. Т.е.
стремится к , но не достигает значения .
Замечание 2. Если при стремлении к
переменная принимает лишь значения меньшие
, или, наоборот, лишь значения, большие и
при этом функция стремится к некоторому
числу A , то говорят об односторонних пределах
функции соответственно слева
и справа
стремится к , но не достигает значения .
Замечание 2. Если при стремлении к
переменная принимает лишь значения меньшие
, или, наоборот, лишь значения, большие и
при этом функция стремится к некоторому
числу A , то говорят об односторонних пределах
функции соответственно слева
и справа
Слайд 8Односторонние пределы
Определение 3. Число A называется левым (правым) пределом функции
в точке a (или при
), если для любого сколь угодно малого положительного числа найдется отвечающее ему положительное число такое, что для всех значений аргумента , удовлетворяющих условию
( ),справедливо неравенство:
Используют символику:
), если для любого сколь угодно малого положительного числа найдется отвечающее ему положительное число такое, что для всех значений аргумента , удовлетворяющих условию
( ),справедливо неравенство:
Используют символику:
для правого предела,
для левого предела.
Слайд 9Определение 4. Говорят, что функция
имеет
в точке a предел
если для любого положительного числа M можно
указать отвечающее ему положительное число
такое, что для всех значений аргумента ,
удовлетворяющих условию
справедливо неравенство:
При этом используют символику:
если для любого положительного числа M можно
указать отвечающее ему положительное число
такое, что для всех значений аргумента ,
удовлетворяющих условию
справедливо неравенство:
При этом используют символику:
Слайд 10
Бесконечно малые величины их свойства
Определение 4. Функция
называется бесконечно малой величиной при , если ее предел равен нулю:
Теорема 1. Если функция имеет при предел, равный A , то ее можно представить в виде суммы этого числа A и бесконечно малой величины при
, т.е.
Теорема 1. Если функция имеет при предел, равный A , то ее можно представить в виде суммы этого числа A и бесконечно малой величины при
, т.е.
Слайд 11Теорема 2. Если функцию
можно представить как сумму числа A и
бесконечно малой величины при
, то число A есть предел
этой функции при , т.е.
Слайд 12Основные свойства бесконечно малых величин
1. Алгебраическая сумма конечного числа бесконечно малых
величин есть величина бесконечная малая.
2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая.
3. Частное от деления бесконечно малой величины на функцию, предел которого отличен от нуля, есть величина бесконечно малая.
2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая.
3. Частное от деления бесконечно малой величины на функцию, предел которого отличен от нуля, есть величина бесконечно малая.
Слайд 13ОСНОВНЫЕ СВОЙСТВА ПРЕДЕЛА
1)
2) Справедливо равенство (первый замечательный предел):
3) Если
4) Справедливо
равенство (второй замечательный предел):
то
( или
),
где
- основание натурального логарифма,
;
Слайд 145) Если
Если существуют конечные пределы:
то справедливы следующие
равенства:
6)
7)
8)
6)
7)
8)
то
, если
Слайд 16а) Если при замене на
под знаком предела получают определенное число, то оно и будет значением предела:
б) Если при замене на под знаком предела получают
в) Если при замене на под знаком предела получают
б) Если при замене на под знаком предела получают
в) Если при замене на под знаком предела получают
где c − число, то
то говорят, что под знаком предела неопределенность.
Слайд 17В таком случае задача вычисления предела
сводится к раскрытию неопределенности:
тождественными преобразованиями «убирают» неопределенность, если это возможно, и вычисляют предел.
Слайд 18Примеры
П р и м е р 1. Вычислить предел:
П
р и м е р 2. Вычислить предел:
Р е ш е н и е:
Р е ш е н и е:
Слайд 19П р и м е р 3. Вычислить предел:
П
р и м е р 4. Вычислить: предел
Р е ш е н и е:
.
Р е ш е н и е:
Слайд 23Непрерывность функции.
О п р е д е л е н
и е 1. Функция называется непрерывной в точке , принадлежащей области определения , если функция имеет в точке конечный предел, равный числу , то есть
О п р е д е л е н и е 2. Функция называется непрерывной справа (слева) в точке из , если в точке существует конечный правый (левый) предел функции, равный числу , то есть
О п р е д е л е н и е 2. Функция называется непрерывной справа (слева) в точке из , если в точке существует конечный правый (левый) предел функции, равный числу , то есть
Слайд 24Из свойств предела вытекает следующее утверждение.
Т е о р е м
а 1. Функция непрерывна в точке a тогда и только тогда, когда в этой точке справедливы равенства:
Слайд 26О п р е д е л е н и е
3. Функция называется непрерывной в интервале , если она непрерывна в любой его точке.
Функция называется непрерывной на отрезке , если она непрерывна в интервале , непрерывна справа в точке непрерывна слева в точке .
Функция называется непрерывной на отрезке , если она непрерывна в интервале , непрерывна справа в точке непрерывна слева в точке .
Слайд 27Точки разрыва функции
О п р е д е л е н
и е . Точка , являющаяся предельной точкой множества , называется точкой разрыва функции , если в точке эта функция либо не определена, либо определена, но нарушено условие непрерывности.
Слайд 28О п р е д е л е н и е.
Точка разрыва называется точкой устранимого разрыва функции , если в этой точке предел функции существует, но в точке либо не определена, либо значение не совпадает с найденным пределом, то есть
Пример: Функция
Пример: Функция
при х =0
при х =0
Имеет в точке х=0 устранимый разрыв, т.к:
Слайд 29О п р е д е л е н и е
. Точка разрыва называется точкой разрыва первого рода функции , если в этой точке функция имеет конечные, но не равные друг другу правый и левый пределы, то есть:
Пример:
«знак» числа х имеет в точке х=0 разрыв первого рода, т.к:
Пример:
«знак» числа х имеет в точке х=0 разрыв первого рода, т.к:
Слайд 30
у
х
1
-1
0
О п р е д е
л е н и е . Точка разрыва
называется точкой разрыва второго рода функции
если в этой точке функция не имеет, по крайней мере, одного из односторонних пределов или хотя бы один из односторонних пределов равен бесконечности.
Слайд 31Пример. Функция имеет в
точке х=0 разрыв второго рода, так как в данном случае число y(0) не определено
у
х
0
Слайд 32Т е о р е м а 1. Если функция
непрерывна в точке и существует конечный предел , то справедливо равенство:
Т е о р е м а 2. Сумма, разность, произведение, частное, суперпозиция конечного числа непрерывных функций (то есть любая элементарная функция) есть функция, непрерывная во всех точках области определения.
Т е о р е м а 2. Сумма, разность, произведение, частное, суперпозиция конечного числа непрерывных функций (то есть любая элементарная функция) есть функция, непрерывная во всех точках области определения.
