- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Предел функции. Непрерывность функций одной переменной презентация
Содержание
- 1. Предел функции. Непрерывность функций одной переменной
- 2. Лекция 2.1 Два определения предела функции в
- 3. Два определения предела функции в точке
- 4. Примеры. 1. 2. Предела нет!!!
- 5. ОПРЕДЕЛЕНИЕ 2 ( Коши ). a A
- 6. Свойства функций, имеющих предел ТЕОРЕМА 2. Если
- 7. ТЕОРЕМА 4. ( О переходе к пределу
- 9. Односторонние пределы.
- 10. ПРИМЕР. Доказать в качестве
- 11. Пределы функции при стремлении аргумента к бесконечности
- 12. Бесконечно малые и бесконечно большие функции
- 13. Свойства бесконечно малых и бесконечно больших функций.
- 14. Введем обозначения: С = const ≠ 0;
- 15. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 2Лекция 2.1
Два определения предела функции в точке, их эквивалентность.
Свойства функций,
Односторонние пределы и пределы при стремлении аргумента к бесконечности.
Бесконечно малые и бесконечно большие функции.
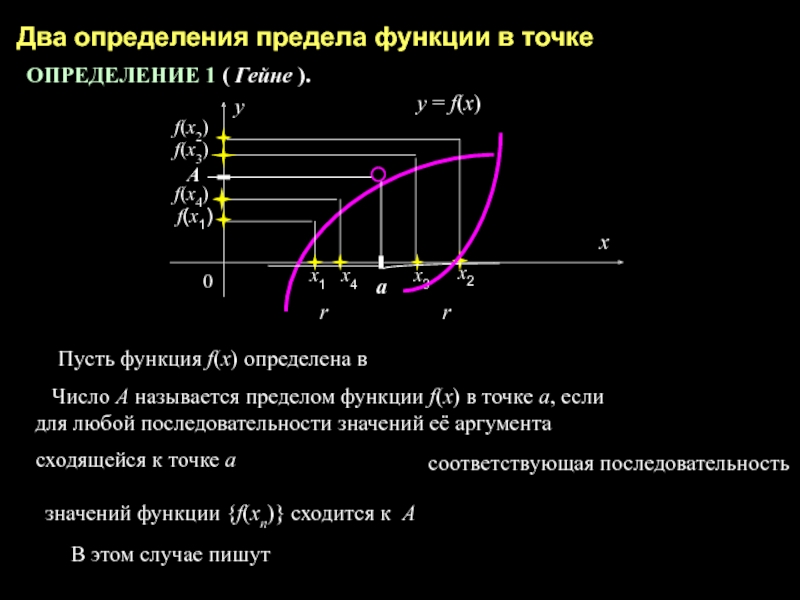
Слайд 3Два определения предела функции в точке
ОПРЕДЕЛЕНИЕ 1 ( Гейне ).
x1
a
A
f(x1)
x2
x3
x4
f(x2)
f(x3)
f(x4)
x
y
y
0
r
r
Пусть функция f(x) определена в
Число А называется пределом функции f(x) в точке а, если
для любой последовательности значений её аргумента
сходящейся к точке а
соответствующая последовательность
значений функции {f(хn)} сходится к А
В этом случае пишут
Слайд 5ОПРЕДЕЛЕНИЕ 2 ( Коши ).
a
A
x
y
y = f(x)
0
A - ε
A + ε
a
a - δ
Пусть функция f(x) определена в
⎢f(x) – A ⎢< ε.
Геометрический аналог определения:
ТЕОРЕМА 1.
Два определения предела функции, по Коши и по Гейне, эквивалентны.
Слайд 6Свойства функций, имеющих предел
ТЕОРЕМА 2.
Если f(x) имеет предел в точке а,
в которой функция ограничена.
Доказательство.
(По опред. предела)
A - 1 < f(x) < A + 1.
Доказательство.
(По опред. предела)
Т.е. f(x) ограничена на множестве
Т.е. f(x) > A/2 > 0.
ТЕОРЕМА 3.
СЛЕДСТВИЕ.
(Об ограниченности функции, имеющей предел.)
(О сохранении функцией знака предела.)
Слайд 7ТЕОРЕМА 4. ( О переходе к пределу в неравенстве)
Доказательство. Воспользуемся определением
Доказательство. Воспользуемся определением предела по Гейне.
Следовательно, по соответствующей теореме для ЧП, А ≥ 0.
ТЕОРЕМА 5. (О двух милиционерах.)
Следствие.
Слайд 8
ТЕОРЕМА 6. (Арифметические свойства пределов функций)
1.
2.
Доказательство.
Докажем свойство 2в.
Воспользуемся опр. предела по
СЛЕДСТВИЕ из теорем 4, 6.
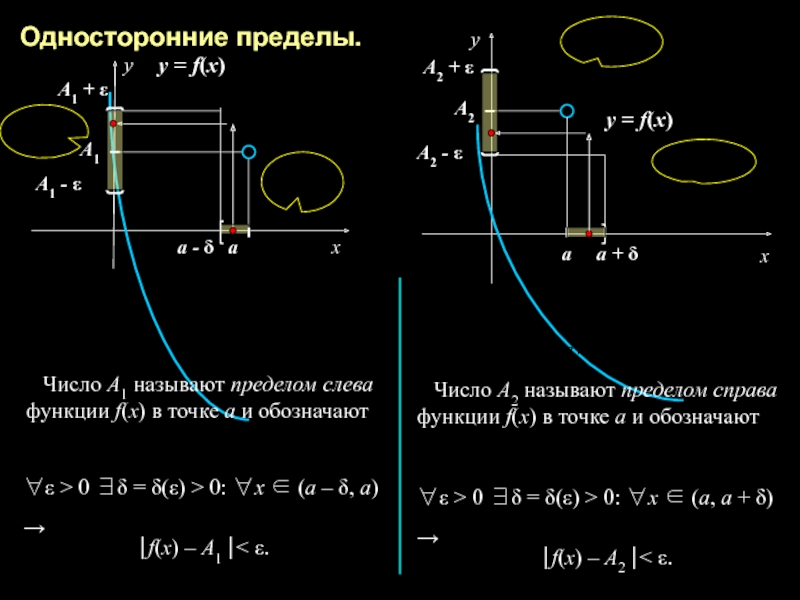
Слайд 9Односторонние пределы.
a
a - δ
A1
A1 + ε
x
y = f(x)
A1 - ε
y
x
y
a
A2
A2
A2 - ε
a + δ
y = f(x)
∀ε > 0 ∃δ = δ(ε) > 0: ∀х ∈ (а – δ, a) →
∀ε > 0 ∃δ = δ(ε) > 0: ∀х ∈ (а, a + δ) →
Число А1 называют пределом слева
функции f(x) в точке а и обозначают
⎢f(x) – A1 ⎢< ε.
Число А2 называют пределом справа
функции f(x) в точке а и обозначают
⎢f(x) – A2 ⎢< ε.
Слайд 10
ПРИМЕР.
Доказать в качестве упражнения:
существовали пределы этой функции в точке а слева
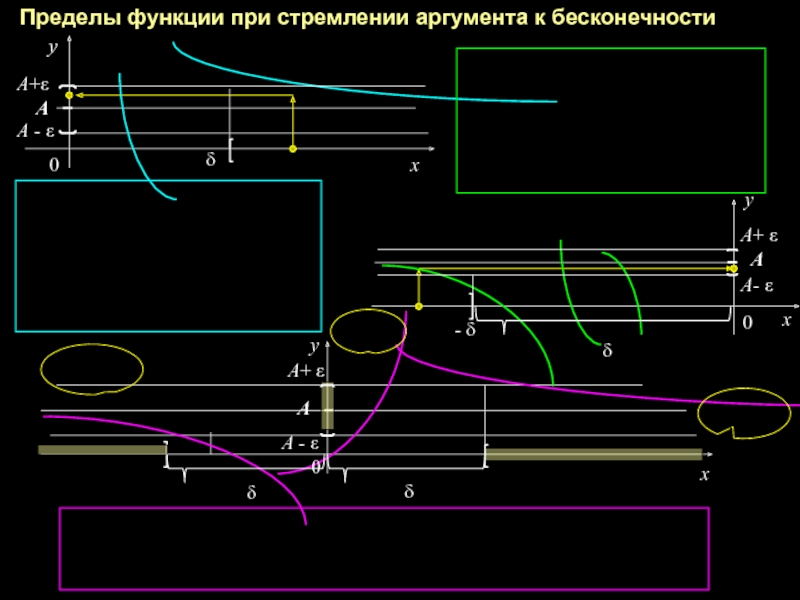
Слайд 11Пределы функции при стремлении аргумента к бесконечности
A
A+ε
A - ε
- δ
δ
x
y
0
A
A+ ε
y
A
δ
δ
x
0
0
A
A+ ε
A- ε
x
y
δ
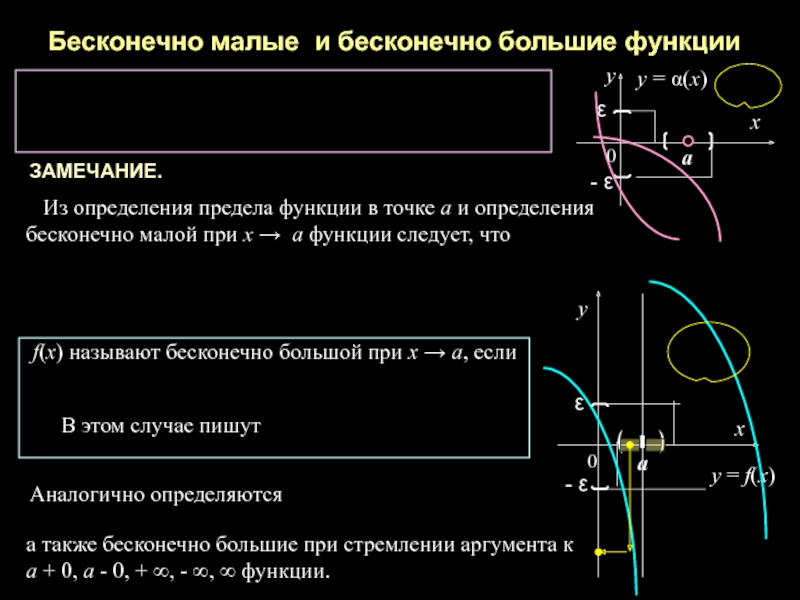
Слайд 12Бесконечно малые и бесконечно большие функции
0
ε
- ε
x
a
y
y = f(x)
f(х) называют бесконечно
В этом случае пишут
a
0
- ε
ε
y
x
ЗАМЕЧАНИЕ.
Из определения предела функции в точке а и определения
бесконечно малой при х → а функции следует, что
Аналогично определяются
а также бесконечно большие при стремлении аргумента к
а + 0, а - 0, + ∞, - ∞, ∞ функции.
y = α(x)
Слайд 13Свойства бесконечно малых и бесконечно больших функций.
Алгебраическая сумма конечного числа бесконечно
Произведение бесконечно малой при х→ а функции на ограниченную в некоторой проколотой окрестности точки а функцию есть бесконечно малая при х→ а функция.
Пусть α(х) ≠ 0 в
α(х) – бесконечно малая при х → а функция тогда и только тогда, когда 1/α(х) – бесконечно большая при х → а.
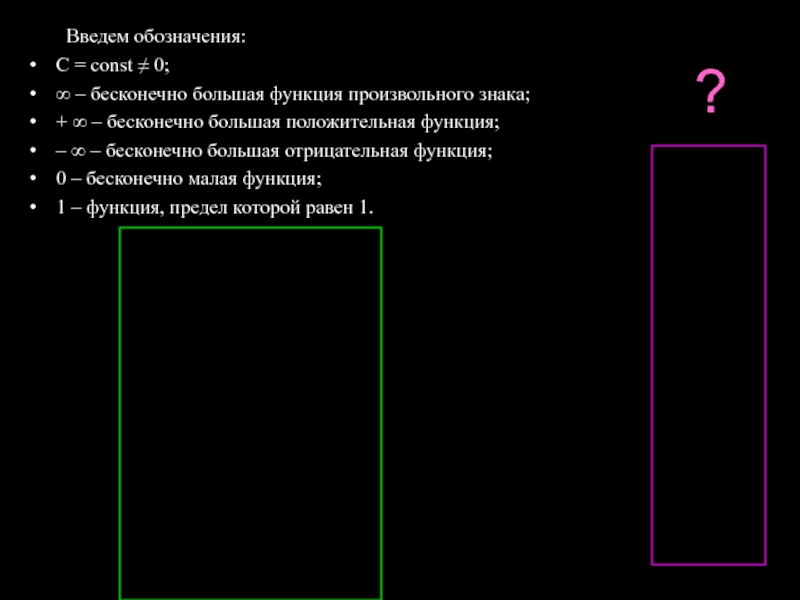
Слайд 14 Введем обозначения:
С = const ≠ 0;
∞ – бесконечно большая функция произвольного
+ ∞ – бесконечно большая положительная функция;
– ∞ – бесконечно большая отрицательная функция;
0 – бесконечно малая функция;
1 – функция, предел которой равен 1.
?